Центральная предельная теорема
Примеры использования ЦПТ
Пример 72. Задача из примера 71. Требуется найти

 ,
, 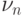 - число выпадений герба.
Вычислим вероятность дополнительного события. Домножим обе части
неравенства под знаком вероятности на
- число выпадений герба.
Вычислим вероятность дополнительного события. Домножим обе части
неравенства под знаком вероятности на  и поделим на
и поделим на 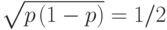 .
.
 :
:
Центральной предельной теоремой пользуются для приближенного вычисления вероятностей, связанных с суммами большого числа независимых и одинаково распределенных величин. При этом распределение центрированной и нормированной суммы заменяют на стандартное нормальное распределение. Насколько велика ошибка при такой замене (погрешность приближения)?
Упражнение. Какие еще предельные теоремы для схемы Бернулли вы знаете? Что такое теорема Пуассона? Найти ее. Какова погрешность пуассоновского приближения? Вычислить ее. Объяснить, почему теорема Пуассона не применима в задаче из примера 72.
В примере 72 мы вычислили вероятность приближенно. Следующий результат позволяет оценить погрешность приближения в ЦПТ.
Теорема 42 (неравенство Берри - Эссеена).
В условиях ЦПТ для любого 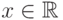 и для любого распределения
и для любого распределения 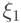 с конечным третьим моментом
с конечным третьим моментом
![\left| \Prob\left(\frac{\displaystyle S_n -
n{\mathsf E\,}\xi_1}{\sqrt{\smash[b]{\mathstrut n\,{\mathsf D\,}\xi_1}}}
<x\right) - \Phi_{0,1}(x) \right|
\le
C\cdot \frac{{\mathsf E\,}{\displaystyle |\xi_1-{\mathsf E\,}\xi_1|}^3}
{\sqrt{\smash[b]{\mathstrut n}}{\bigl(\sqrt{\smash[b]{\mathstrut
{\mathsf D\,}\xi_1}}\,\bigr)}^3}.](/sites/default/files/tex_cache/9f5666956693aa35afe8140586654f3b.png)
Замечание.
В качестве постоянной  можно брать число
можно брать число  .
.
Продолжение примера 72
Проверьте,
что для случайной величины 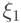 с распределением Бернулли
с распределением Бернулли

 " в примере 72
при
" в примере 72
при  и
и  не превышает величины
не превышает величины![C\cdot
\frac{p\mspace{2mu}q(p^2+q^2)}{\sqrt{\smash[b]{npq}}{\left(\sqrt{\smash[b]{pq}}\right)}^3}=
C\cdot \frac{p^2+q^2}{\sqrt{\smash[b]{\mathstrut
n\vphantom{pq}}}\,\sqrt{\smash[b]{pq}}}\le 0{,}4\cdot
\frac{1}{100}=0{,}004,](/sites/default/files/tex_cache/ff7e940e24fff376da4b5cf71e26133d.png)
 не больше, чем
не больше, чем  .
Уместно сравнить этот ответ с оценкой
.
Уместно сравнить этот ответ с оценкой  , полученной
с помощью ЗБЧ
в примере 71.
, полученной
с помощью ЗБЧ
в примере 71.
