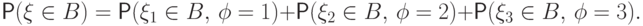Случайные величины и их распределения
Теорема 20.
Если функция  обладает свойствами (f1) и
(f2),
то существует вероятностное пространство и случайная величина
обладает свойствами (f1) и
(f2),
то существует вероятностное пространство и случайная величина  на нем, для которой
на нем, для которой  является плотностью распределения.
является плотностью распределения.
Доказательство.
Пусть  - область, заключенная между осью абсцисс
и графиком функции
- область, заключенная между осью абсцисс
и графиком функции  .
Площадь области
.
Площадь области  равна единице по свойству (f2).
Возьмем в качестве
равна единице по свойству (f2).
Возьмем в качестве 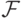 множество борелевских подмножеств
множество борелевских подмножеств  ,
а в качестве вероятности
,
а в качестве вероятности 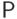 -
меру Лебега (площадь) на множествах из
-
меру Лебега (площадь) на множествах из 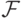 .
И пусть случайная величина
.
И пусть случайная величина  - абсцисса точки, наудачу
брошенной
в эту область.
Тогда
для любого
- абсцисса точки, наудачу
брошенной
в эту область.
Тогда
для любого 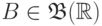 выполнено
выполнено
![\begin{equation}\Prob(\xi\in B) = \Prob(\text{точка попала в } D_B)=
\frac{\text{ площадь } D_B}{\text{ площадь } \Omega}
= \smash{\int\limits_B}\; f(x) dx.
\end{equation}
\begin{figure}[h]
\centering{
}
\end{figure}](/sites/default/files/tex_cache/bb761f1015ef0171ea2f86e58b924e89.png) |
( 6.2) |
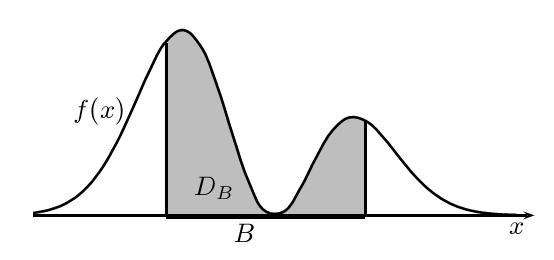
Здесь область 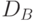 есть криволинейная трапеция с основанием
есть криволинейная трапеция с основанием  под графиком плотности (
рис.
6.1).
По определению, равенство (6.2)
означает, что функция
под графиком плотности (
рис.
6.1).
По определению, равенство (6.2)
означает, что функция  является плотностью распределения
величины
является плотностью распределения
величины  .
.
Отметим полезное свойство абсолютно непрерывных распределений.
Свойство 7.
Если случайная величина  имеет абсолютно непрерывное
распределение, то
имеет абсолютно непрерывное
распределение, то  для любого
для любого 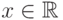 .
.
Доказательство сразу следует из определения 24 и следующего за ним замечания: интеграл по области интегрирования, состоящей из одной точки, равен нулю.
Можно выделить еще один особый класс распределений, сосредоточенных, в отличие от абсолютно непрерывных распределений, на множестве нулевой меры Лебега, но не имеющих, в отличие от дискретных, атома ни в одной точке этого множества.
Определение 25.
Случайная величина  имеет сингулярное
распределение, если существует борелевское множество
имеет сингулярное
распределение, если существует борелевское множество  с нулевой лебеговой мерой
с нулевой лебеговой мерой  такое,
что
такое,
что  , но при этом
, но при этом  для любой точки
для любой точки  .
.
Можно отметить следующее свойство сингулярных распределений. Множество  , на котором
сосредоточено все распределение, не может состоять из конечного или счетного
числа точек. Действительно,
если
, на котором
сосредоточено все распределение, не может состоять из конечного или счетного
числа точек. Действительно,
если  конечно или счетно, то
конечно или счетно, то 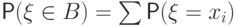 , где суммирование ведется
по всем
, где суммирование ведется
по всем  . Последняя сумма равна нулю как сумма счетного
числа нулей,
что противоречит предположению
. Последняя сумма равна нулю как сумма счетного
числа нулей,
что противоречит предположению  .
.
Таким образом, любое сингулярное распределение сосредоточено на несчетном множестве с нулевой мерой Лебега. Примером такого множества может служить канторовское совершенное множество, а примером такого распределения - лестница Кантора (см. ниже).
Наконец, распределение может быть выпуклой линейной комбинацией дискретного, абсолютно непрерывного и сингулярного распределений.
Определение 26.
Случайная величина  имеет смешанное
распределение, если найдутся такие случайные величины
имеет смешанное
распределение, если найдутся такие случайные величины 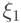 ,
, 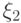 и
и  - с дискретным,
абсолютно
непрерывным и сингулярным распределениями соответственно (или такие три
распределения), и
числа
- с дискретным,
абсолютно
непрерывным и сингулярным распределениями соответственно (или такие три
распределения), и
числа 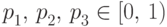 ,
, 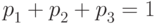 , что для любого
, что для любого 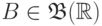 имеет место равенство
имеет место равенство

По заданным на одном вероятностном пространстве случайным величинам 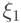 ,
, 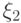 ,
,  и числам
и числам 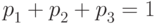 можно построить
случайную
величину со смешанным распределением так: пусть
можно построить
случайную
величину со смешанным распределением так: пусть  -
случайная
величина на том же вероятностном пространстве с дискретным распределением
-
случайная
величина на том же вероятностном пространстве с дискретным распределением 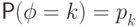 для
для  , и
пусть
при любом
, и
пусть
при любом  и любом
и любом 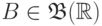 события
события 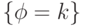 и
и  независимы.
независимы.
Построим случайную величину  так: если
так: если  , то положим
, то положим 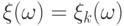 .
Ее распределение найдем по формуле полной вероятности:
.
Ее распределение найдем по формуле полной вероятности: