Предварительные сведения
Операции над событиями. В теории вероятностей рассматривают те же операции над событиями (множествами), что и в теории множеств. Дадим определения новым событиям - результатам этих операций.
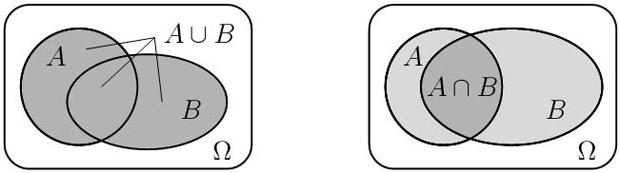
Объединением 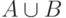 событий
событий  и
и 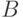 называется событие, состоящее в том, что из двух событий
называется событие, состоящее в том, что из двух событий  и
и 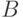 случилось хотя бы одно. Это событие включает как элементарные исходы из
множества
случилось хотя бы одно. Это событие включает как элементарные исходы из
множества 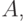 так и элементарные исходы из множества
так и элементарные исходы из множества 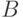 (
рис.
1.1).
(
рис.
1.1).
Пересечением 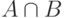 событий
событий  и
и 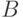 называется событие, состоящее в том, что произошли
сразу оба события
называется событие, состоящее в том, что произошли
сразу оба события  и
и  ., Это событие содержит элементарные исходы,
каждый из которых принадлежит и множеству
., Это событие содержит элементарные исходы,
каждый из которых принадлежит и множеству 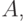 и множеству
и множеству  .
Вместо
.
Вместо 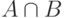 часто пишут просто
часто пишут просто 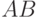 .
.
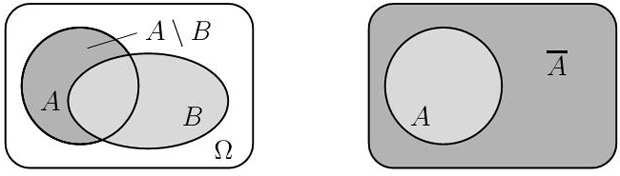
Дополнением  события
события  до
до  называется событие, состоящее в том, что произошло
называется событие, состоящее в том, что произошло  , но не произошло
, но не произошло  .
Событие
.
Событие  содержит элементарные исходы, входящие
в множество
содержит элементарные исходы, входящие
в множество  , но не входящие в
, но не входящие в  .
.
Противоположным (или дополнительным)
к событию  называется событие
называется событие 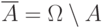 ,
состоящее в том, что
,
состоящее в том, что  не произошло.
Событие
не произошло.
Событие 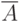 состоит из элементарных исходов, не входящих
в множество
состоит из элементарных исходов, не входящих
в множество  (
рис.
1.2).
(
рис.
1.2).
Выделим среди подмножеств  два особых события.
два особых события.
Достоверным называется
событие, которое обязательно происходит в результате эксперимента,
т. е. единственное событие, включающее все элементарные исходы - событие  .
.
Невозможным называется
событие, которое не может произойти в результате эксперимента,
т. е. событие, не содержащее ни одного элементарного исхода -
"пустое множество"  .
.
Очевидны следующие равенства: 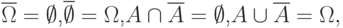
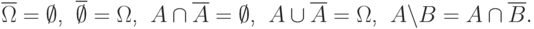
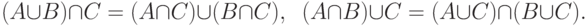
Кроме того, объединение и пересечение событий связаны очень важными соотношениями двойственности:
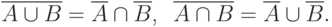
Пример 8.
Пусть событие 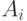 означает, что
означает, что 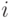 -я деталь бракованная, где
-я деталь бракованная, где 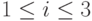 -
номер детали.
Запишем с помощью операций над событиями
событие
-
номер детали.
Запишем с помощью операций над событиями
событие  - "ровно две из трех деталей бракованные":
- "ровно две из трех деталей бракованные":

Событие 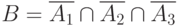 , означает "все три детали годные".
, означает "все три детали годные".
Событие "хотя бы одна деталь из трех бракованная" можно записать двумя способами: 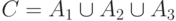 и
и  . Равносильность этих двух выражений следует из формул двойственности.
. Равносильность этих двух выражений следует из формул двойственности.
Отношения между событиями. Множества могут пересекаться или не пересекаться, быть включены одно в другое или не быть. В теории вероятностей эти отношения событий носят особые названия.
События  и
и 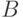 называются несовместными,
если они не могут произойти одновременно:
называются несовместными,
если они не могут произойти одновременно: 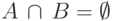 .
.
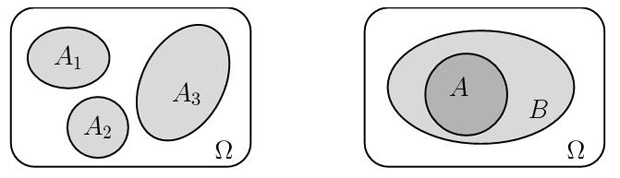
События  называются попарно несовместными,
если несовместны любые два из них, т. е.
называются попарно несовместными,
если несовместны любые два из них, т. е. 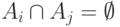 для любых
для любых 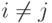 .
.
Говорят, что событие  влечет событие
влечет событие 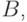 и пишут
и пишут 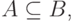 если всегда, как только происходит событие
если всегда, как только происходит событие 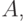 происходит и событие
происходит и событие  . Это означает,
что любой элементарный исход, входящий в множество
. Это означает,
что любой элементарный исход, входящий в множество 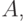 одновременно входит в множество
одновременно входит в множество 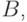 т. е.
т. е.  содержится в
содержится в 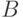 (
рис.
1.3)
(
рис.
1.3)
Пример 9. При бросании двух игральных костей события "сумма очков равна четырем" и "на первой кости выпало шесть очков" несовместны: они не могут случиться одновременно.
Событие "сумма очков равна двум" влечет за собой событие "на костях выпало одинаковое число очков". Действительно, сумма очков равна двум лишь при выпадении двух единиц. Но тогда на костях выпадет одинаковое число очков. Обратное включение неверно: не всегда, когда на костях выпадает одинаковое число очков, сумма этих очков равна двум.
Событие "сумма очков меньше пяти" влечет за собой событие "сумма очков меньше семи".