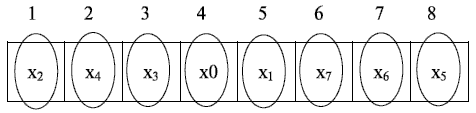Размещение элементов электрической схемы
20.5. Итерационные алгоритмы улучшения начального размещения
Алгоритмы данной группы используют общие идеи методов последовательных приближений и являются комбинаторными аналогами градиентных методов оптимизации. Для этих алгоритмов необходимо задать начальный вариант размещения.
Итерационные алгоритмы применяются для решения задачи размещения с различными критериями оптимизации 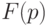 : суммарная длина соединений, суммарное число пересечений соединений и т.д.
: суммарная длина соединений, суммарное число пересечений соединений и т.д.
В любом итерационном алгоритме исследуется подмножество размещений, в некотором смысле близких к начальному, для выделения в нём размещения с меньшим значением функции - критерия. Найденное размещение вновь принимается за начальное, и процесс повторяется.
Алгоритм завершается при отыскании некоторого размещения, в окружности которого отсутствуют варианты с меньшим значением функций - критерия. В большинстве случаев такой процесс приводит к получению локального минимума функции 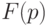 .
.
Пусть, 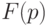 - некоторая функция - критерий размещения, а
- некоторая функция - критерий размещения, а  - начальное размещение.
- начальное размещение.
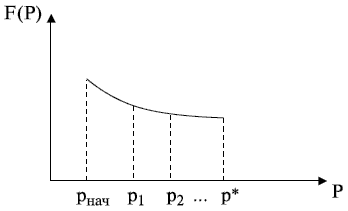
Тогда в результате применения итерационного алгоритма размещения получается последовательность размещений 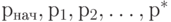 , которой соответствует монотонно убывающая последовательность значений
, которой соответствует монотонно убывающая последовательность значений 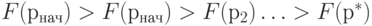 (рис. 20.5).
(рис. 20.5).
Значение  соответствует локальному минимуму функции.
Практика применения подобных алгоритмов показывает, что получаемые размещения близки к оптимальным.
Это связано с тем, что используемые критерии оптимизации
соответствует локальному минимуму функции.
Практика применения подобных алгоритмов показывает, что получаемые размещения близки к оптимальным.
Это связано с тем, что используемые критерии оптимизации 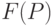 являются относительно пологими функциями, не имеющими " острых " экстремумов.
являются относительно пологими функциями, не имеющими " острых " экстремумов.
Характерной чертой итерационного алгоритма является возможность получения варианта размещения в любой момент итерационного процесса. При реализации алгоритма на ЭВМ, как правило, итерационный процесс заканчивается, как только разность значений функций - критерия для двух соседних итераций становится относительно малой:
![[ F(р_{k}) - F ( р_{k-1 }) ] / F ( р_{k }) < \delta,](/sites/default/files/tex_cache/7e4f137015f47403b435337c3a5bf474.png) |
( 20.12) |
где  - заранее заданное число.
- заранее заданное число.
Различные итерационные алгоритмы размещения имеют сходную структуру, содержащую следующие элементы:
- преобразование очередного размещения;
- вычисление функции размещения;
- выбор лучшего размещения;
- переход к следующей итерации и правило остановки.
В качестве начального может быть взято размещение, полученное одним из конструктивных алгоритмов размещения, с помощью генератора случайных размещений или заданное конструктором.
Из-за отсутствия теоретических оценок эффективности различных итерационных алгоритмов невозможно отдать явное предпочтение одному из них. Поэтому рассмотрим один из наиболее распространенных методов, эффективность которого подтверждается при решении практических задач.
Алгоритм парных перестановок
Алгоритмы парных перестановок являются простейшими в рассматриваемом классе алгоритмов размещения.
Пусть, имеется некоторое размещение (начальное или результат предыдущей итерации). Выбираются два элемента  и
и 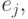 которые затем меняются местами.
которые затем меняются местами.
Рассчитывается новое значение 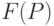 ; если оно меньше прежнего, то производится обмен.
Выбирается другая пара элементов и осуществляется аналогичная процедура.
Процесс итеративно продолжается до тех пор, пока не будет применено используемое в алгоритме правило остановки.
; если оно меньше прежнего, то производится обмен.
Выбирается другая пара элементов и осуществляется аналогичная процедура.
Процесс итеративно продолжается до тех пор, пока не будет применено используемое в алгоритме правило остановки.
Пример. Рассмотрим минимизацию суммарной длины соединений:
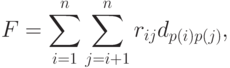 |
( 20.13) |
где 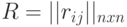 и
и 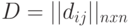 - соответственно, матрицы соединений и расстояний.
- соответственно, матрицы соединений и расстояний.
Найдем приращение значения функции (21.13) при перестановке местами элементов  и
и  , находящихся первоначально в позициях "
, находящихся первоначально в позициях "  " и
"
" и
"  ", соответственно.
", соответственно.
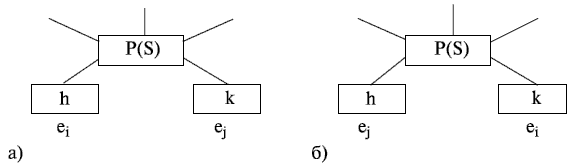
На рис. 20.6. показано положение этих элементов до и после перестановки, а также их связи с некоторым элементом  , не участвующим в перестановке и находящимся в позиции
, не участвующим в перестановке и находящимся в позиции 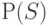 .
.
Если длину соединений между всеми парами элементов, не затрагиваемых данной перестановкой, обозначить через
"  ", то получим следующее выражение для суммарной длины соединений
", то получим следующее выражение для суммарной длины соединений
 |
( 20.14) |
После перестановки местами элементов  и
и 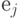 значение суммарной длины изменится и станет равным:
значение суммарной длины изменится и станет равным:
 |
( 20.15) |
Сравнивая (20.14) и (20.15), можно подсчитать приращение функции
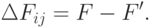 |
( 20.16) |
После некоторых преобразований получим
 |
( 20.17) |
Алгоритмы парных перестановок для минимизации суммарной длины соединений отличаются как способом определения исследуемой окрестности очередного варианта размещения, так и стратегией выбора следующего варианта с меньшим значением длины соединений.
Очередная пара элементов для перестановки выбирается либо случайно, либо, что более эффективно, некоторым систематическим образом.
На очередной итерации для каждого элемента 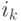 в последовательности
в последовательности  рассчитывается приращение
рассчитывается приращение 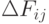 (20.17) , при условии перестановки этого элемента с элементами, стоящими правее в последовательности
(20.17) , при условии перестановки этого элемента с элементами, стоящими правее в последовательности  .
.
После расчёта всех характеристик 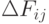 выбирается максимальное положительное значение
выбирается максимальное положительное значение 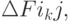 и элемент
и элемент  меняется местами с соответствующим элементом
последовательности
меняется местами с соответствующим элементом
последовательности 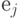 .
.
Если для данного элемента 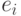 в наборе
в наборе 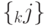 отсутствуют положительные приращения, он оставляется на своём месте и осуществляется переход к отысканию "наилучшего" места для следующего элемента
отсутствуют положительные приращения, он оставляется на своём месте и осуществляется переход к отысканию "наилучшего" места для следующего элемента 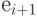 .
.
По окончании очередной итерации получается размещение с меньшей длиной соединений и осуществляется переход к следующей итерации.
Итерационный процесс заканчивается, когда изменение общей длины соединений в соответствии с (20.12) становится относительно малым.
Рассмотрение на каждой итерации возможных перестановок связано со значительными временными затратами. Поэтому в ряде алгоритмов на каждой итерации исследуются лишь перестановки соседних элементов. Кроме сокращения количества рассчитываемых приращений (оно становится пропорциональным  ) упрощается и вычисление самих приращений.
) упрощается и вычисление самих приращений.
Продолжим расчет для нашего примера. Попытаемся улучшить критерий размещения, полученный после применения последовательного алгоритма (рис. 20.4).
Первый шаг. Берем элемент  ,
условно меняем местами со всеми остальными элементами, кроме фиксированного
,
условно меняем местами со всеми остальными элементами, кроме фиксированного 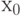 ,
и рассчитываем приращение (20.4) относительно
,
и рассчитываем приращение (20.4) относительно 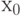 :
:

Так как 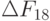 получилось положительным, то меняем местами
получилось положительным, то меняем местами  и
и 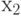 .
Элемент
.
Элемент 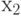 помещаем в первую позицию:
помещаем в первую позицию:
Тогда 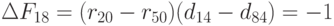 .
Значение получилось отрицательным, элементы так и оставляем.
.
Значение получилось отрицательным, элементы так и оставляем.
Второй шаг. На втором шаге меняем местами элемент 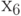 со всеми остальными элементами, кроме
со всеми остальными элементами, кроме 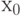 и
и 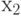 , и рассчитываем приращения относительно уже двух этих фиксированных элементов:
, и рассчитываем приращения относительно уже двух этих фиксированных элементов:
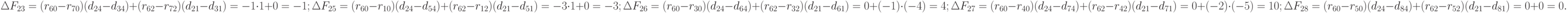
Так как 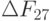 получилось наибольшим положительным, то меняем местами
получилось наибольшим положительным, то меняем местами 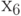 с элементом
с элементом 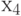 , который находится в седьмой позиции, получаем:
, который находится в седьмой позиции, получаем:

переходим к следующему шагу.
Третий шаг. Аналогично проводим расчеты для оставшихся элементов.

Так как 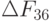 получилось наибольшим положительным, то меняем местами
получилось наибольшим положительным, то меняем местами 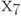 и
и 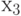 .
.
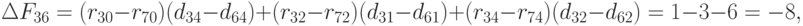
переходим к следующему шагу.
Четвертый шаг.
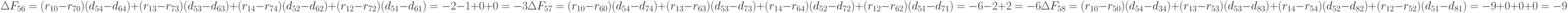
Элемент 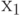 остаётся неизменным.
остаётся неизменным.
Пятый шаг.
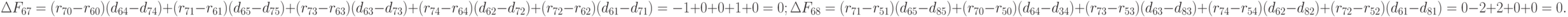
Шестой шаг.

Получили отрицательное число, следовательно, перестановку элементов не производим.
В результате получили окончательное размещение
Рассчитаем критерий размещения после использования итерационного алгоритма
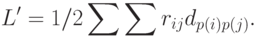 |
( i)p(j)}) |
Для этого вычислим минимальную суммарную взвешенную длину связей между позициями:
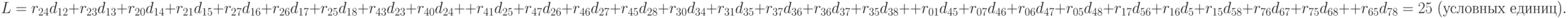
Значение МСВД уменьшилось. Это свидетельствует о том, что данный метод помог улучшить размещение элементов.
Контрольные вопросы
- Что относится к метрическим параметрам конструкции узлов и схем?
- Что относится к топологическим параметрам конструкции узлов и схем?
- Что является главной целью размещения?
- Как рассчитывается главный критерий размещения?
- Что является вариантами коммутационного поля?
- Дайте общую характеристику алгоритмов размещения.
- Как рассчитывается матрица длин D?
- Как решается задача квадратичного назначения?
- Какие предположения делают при решении задачи минимизации СВД?
- Расскажите о работе последовательного алгоритма размещения по связности.
- Что является мерой связности двух элементов?
- Как осуществляется выбор элементов в последовательном алгоритме?
- Как рассчитывается характеристика абсолютной связности?
- Как рассчитывается характеристика относительной связности?
- Как осуществляется выбор позиции в последовательном алгоритме размещения?
- Поясните структуру итерационного алгоритма.
- Как работает итерационный алгоритм парных перестановок?

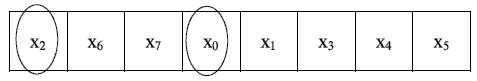



 в
в