Задачи оптимизации как основа для управления качеством промышленной продукции
Основное назначение лекции - показать необходимость и важность роли решения задачи оптимизации в управлении производством и качеством промышленной продукции.
6.1. Постановка и математическая формулировка задачи оптимизации
Проектирование системы и управление технологическим процессом ее изготовления - сложные и трудно формализуемые процедуры, объединяющие такие важные операции, как синтез структуры, выбор параметров элементов, анализ и принятие решений, выбор модели и разработка алгоритмов оперативного управления технологическим процессом.
На первых порах автоматизации проектирования промышленных изделий стремились к созданию оптимальной системы: задача проектирования считалась успешно решенной, если удавалось спроектировать строго допустимую систему. Однако в связи с постоянно возрастающими требованиями к самим изделиям, к их стоимости и времени изготовления появилась необходимость решения таких задач: уменьшить по сравнению с запланированной стоимость системы, время ее разработки и др. Следовательно, стало необходимым не просто удовлетворение исходным требованиям, предъявляемым к показателям качества системы, но и перевыполнение этих требований.
При этом показателем качества 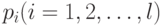 системы является такая числовая характеристика, которая связана с ее качеством строго монотонной зависимостью: чем больше (чем меньше) величина
системы является такая числовая характеристика, которая связана с ее качеством строго монотонной зависимостью: чем больше (чем меньше) величина 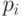 , тем лучше система при прочих равных условиях.
, тем лучше система при прочих равных условиях.
При решении вопроса о том, может ли тот или иной параметр являться показателем качества 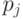 , влияние этого показателя на качество системы должно рассматриваться при прочих равных условиях, например, при сохранении неизменных значений всех остальных признаков. Иначе даже в отношении столь бесспорного показателя, как стоимость, нельзя было бы утверждать, что "чем меньше стоимость, тем лучше система", т. к. при уменьшении стоимости могут уменьшаться какие-либо важнейшие признаки качества.
, влияние этого показателя на качество системы должно рассматриваться при прочих равных условиях, например, при сохранении неизменных значений всех остальных признаков. Иначе даже в отношении столь бесспорного показателя, как стоимость, нельзя было бы утверждать, что "чем меньше стоимость, тем лучше система", т. к. при уменьшении стоимости могут уменьшаться какие-либо важнейшие признаки качества.
Учитывая изложенное, совокупность всех исходных данных, которые имеются к началу оптимизации проектирования, можно разбить на подгруппы.
- Совокупность условий работы системы.
- Совокупность ограничений на структуру и параметры проектируемой системы.
- Совокупность
 показателей качества системы.
показателей качества системы. - Совокупность ограничений, накладываемых на показатели качества.
К условиям работы относятся характеристики полезных сообщений и сигналов, характеристики помех, диапазон рабочих температур, давления, влажности и т. д.
Ограничения, накладываемые на структуру и параметры системы, зависят от решаемой задачи и могут варьироваться от достаточно слабых (система должна быть линейной, стационарной и т. д.) до весьма жестких, когда четко задается принципиальная схема, а в процессе проектирования варьируются только ее параметры заданной схемы.
Ограничения на параметры могут быть типа равенств:
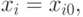 |
( 6.1) |
 |
( 6.2) |
Данные ограничения относятся к прямым ограничениям. Такие ограничения появляются объективно при проектировании технических объектов и вытекают из физической и технологической реализуемости параметров элементов, ограниченности ресурсов и т. д. При постановке задач оптимизации учет ограничений бывает иногда принципиально необходим.
В процессе проектирования системы необходимо учитывать совокупность показателей качества 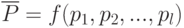 . При формулировке исходных данных определяется лишь состав этой совокупности, т. е. указывается, что именно следует понимать под
. При формулировке исходных данных определяется лишь состав этой совокупности, т. е. указывается, что именно следует понимать под 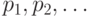 и т. д.; численные же значения составляющих вектора
и т. д.; численные же значения составляющих вектора 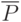 зависят от структуры и параметров системы и в процессе синтеза варьируются.
зависят от структуры и параметров системы и в процессе синтеза варьируются.
На показатели качества также обычно накладываются ограничения, которые представляют собой, как правило, условия, при которых значения выходных параметров ( показателей качества ) соответствуют области работоспособности. Такие ограничения называют функциональными ограничениями. Они тоже могут быть типа равенств:
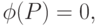 |
( 6.3) |
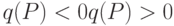 |
( 6.4) |
Прямые и функциональные ограничения формируют допустимую область поиска.
Система (вариант построения системы), удовлетворяющая совокупности условий и ограничений, которые задаются в качестве исходных данных, называется допустимой. В общем случае может существовать не одна, а некоторое множество допустимых систем.
Из всех допустимых необходимо выбрать оптимальную (наилучшую) систему, которая обладает наилучшим (в заранее установленном смысле) значением вектора  показателей качества. Следовательно, для выбора оптимальной системы должен быть предварительно выбран (обоснован) критерий оптимальности (его иначе называют критерием предпочтения). Критерий предпочтения представляет собой правило, на основании которого одно значение вектора
показателей качества. Следовательно, для выбора оптимальной системы должен быть предварительно выбран (обоснован) критерий оптимальности (его иначе называют критерием предпочтения). Критерий предпочтения представляет собой правило, на основании которого одно значение вектора  следует считать лучшим (или худшим) другого его значения.
следует считать лучшим (или худшим) другого его значения.
Следовательно, решение задач оптимизации является одной из важнейших проблем. Оптимизация включает в себя как оптимизацию собственно разрабатываемой системы, так и оптимизацию технологического процесса ее изготовления. Обе эти стороны оптимизации тесно взаимосвязаны. Показатели качества разработанной системы существенно зависят от степени оптимальности процесса разработки и отпущенных на нее времени и средств. В свою очередь, время и средства, затраченные на разработку системы, и сам процесс разработки в значительной степени определяются структурой системы и значениями ее параметров. Однако задача одновременной оптимизации самой системы и процесса ее разработки весьма сложна. Поэтому оптимизация дол жна осуществляться на всех этапах проектирования системы, а также и на последующих этапах ее разработки. Однако в возможно большей степени ее необходимо осуществлять на самых ранних этапах проектирования, а также и разработки технологического процесса изготовления продукции, т. к. при этом оптимизация может быть наиболее радикальной и потребует меньших экономических затрат.
Отыскание оптимальной системы называют синтезом системы.
Как уже отмечалось, любая система или ее часть (устройство, блок, узел) характеризуется совокупностью  показателей качества
показателей качества 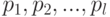 , где число
, где число 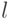 может быть значительно больше единицы. Поэтому задача синтеза формулируется следующим образом: найти такую систему, которая удовлетворяет совокупности исходных данных и обладает при этом значением совокупности (вектора)
может быть значительно больше единицы. Поэтому задача синтеза формулируется следующим образом: найти такую систему, которая удовлетворяет совокупности исходных данных и обладает при этом значением совокупности (вектора)  показателей качества, наилучшим в смысле заранее выбранного критерия оптимальности.
показателей качества, наилучшим в смысле заранее выбранного критерия оптимальности.
Синтез системы осуществляется обычно путем сочетания эвристических и математических методов. Математический синтез заключается в математической формулировке исходных данных и критерия оптимальности (критерия предпочтения) и отыскании математическим путем такого решения (т. е. такой системы), которое обеспечивает получение наилучшего значения вектора 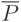 (максимального или минимального в зависимости от конечной цели). Однако математический синтез проводится при многих допущениях, идеализации многих сложных ситуаций. Поэтому задача синтеза обычно решается путем сочетания методов математического синтеза с эвристическим синтезом, который основан на инженерном опыте и интуиции, проведении приближенных расчетов и принятии решений инженером по результатам, полученным после математического синтеза
и на основании своего собственного опыта. Сопоставление и взаимная коррекция данных позволяют получать оптимальные результаты. Такой комбинированный пр
оцесс сочетания, математических и эвристических методов называют инженерным синтезом.
(максимального или минимального в зависимости от конечной цели). Однако математический синтез проводится при многих допущениях, идеализации многих сложных ситуаций. Поэтому задача синтеза обычно решается путем сочетания методов математического синтеза с эвристическим синтезом, который основан на инженерном опыте и интуиции, проведении приближенных расчетов и принятии решений инженером по результатам, полученным после математического синтеза
и на основании своего собственного опыта. Сопоставление и взаимная коррекция данных позволяют получать оптимальные результаты. Такой комбинированный пр
оцесс сочетания, математических и эвристических методов называют инженерным синтезом.
Методы инженерного синтеза больших, средних и малых систем единичного и массового производства и различного назначения бесконечно разнообразны. Однако во всех случаях инженерный синтез должен быть векторным и глобальным.
Векторным называется синтез, производимый с учетом не одного, а нескольких показателей качества, т. е. на основе вектора  (векторная или многокритериальная оптимизация ). В отличие от векторной, оптимизация, проводимая по единственному критерию, называется скалярной.
(векторная или многокритериальная оптимизация ). В отличие от векторной, оптимизация, проводимая по единственному критерию, называется скалярной.
Глобальным называется синтез,производимый с учетом всех существенных показателях качества, включая экономические, физические, конструктивные др. Если при оптимизации учитывается один показатель, то он называется частным.
При инженерном синтезе не может быть ситуации, чтобы был всего один показатель качества: всегда будет не менее двух показателей, которые нельзя не учитывать, - стоимость и основной технический показатель (на самом деле их всегда существует несколько). Отсюда следует, что практически инженерный синтез всегда является векторным и глобальным.
Синтез сложного объекта включает решение следующих основных задач.
- Синтез оптимальной структуры, т. е. отыскание оптимальных принципов построения системы, видов различных устройств, характера их взаимодействия и т. д.
- Выбор оптимальных значений параметров системы, т. е. оптимизация параметров.
- Выбор оптимального варианта построения системы из конечного числа полученных вариантов. Это так называемый дискретный выбор системы.
Следовательно, оптимизация системы включает синтез оптимальной структуры, оптимизацию параметров и дискретный выбор.
Таким образом, инженерный синтез системы представляет собой сочетание всех упомянутых выше методов синтеза - глобального и частного, эвристического и математического, синтеза структуры, оптимизации параметров и дискретного выбора.
Оптимизация заключается в варьировании совокупности параметров системы - вектора  ; при этом требуется найти такую совокупность
; при этом требуется найти такую совокупность 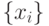 , при которой вектор
, при которой вектор  имеет наилучшее (в смысле выбранного критерия предпочтения) значение. В общем случае каждый из показателей качества
имеет наилучшее (в смысле выбранного критерия предпочтения) значение. В общем случае каждый из показателей качества 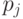 может зависеть от всех "
может зависеть от всех "  " параметров:
" параметров:
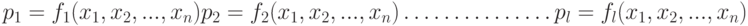 |
( 6.5) |
Эти зависимости называют целевыми функциями.Любая техническая система характеризуется многими свойствами, определяющими ее качество. Среди этих свойств есть такие, величину которых необходимо увеличить; есть и такие, которые следует минимизировать. Следовательно, альтернатива, перед которой оказываются проектировщики систем, в большинстве случаев является многокритериальной.
Сущность системного подхода к выбору целевой функции заключается в следующем. В отличие от однокритериальных задач, в которых оптимальность характеризуется максимумом (или минимумом) единственной целевой функции (т. е. скалярной величиной), в многокритериальных задачах оптимальное решение может представлять собой лишь некоторый компромисс между величиной частных критериев, поскольку каждый из них представляет собой в той или иной мере целевую функцию. Поэтому многокритериальные задачи иногда называют многоцелевыми.
Однако методы исследования операций, используемые при решении задач оптимизации, предполагают наличие одной целевой функции в каждой задаче. Оптимальное решение, которое позволяет найти метод оптимизации, означает максимизацию (или минимизацию) целевой функции. Последняя количественно выражает качество объекта, поэтому ее называют также функцией качества или критерием оптимальности. Выбор такого критерия оптимальности лежит в основе правила предпочтения.
Следовательно, целевая функция должна быть одна, но при этом учитывать все частные критерии качества. Поэтому при решении задач оптимизации осуществляют сведение многокритериальной задачи к однокритериальной. Такая операция называется сверткой векторного критерия.
Тогда вместо векторного критерия 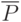 оптимальности в результате применения принципа справедливой абсолютной уступки формируют обобщенный (скалярный, составной) критерий оптимальности.
оптимальности в результате применения принципа справедливой абсолютной уступки формируют обобщенный (скалярный, составной) критерий оптимальности.
Сведение многокритериальной задачи к однокритериальной за счет введения обобщенного критерия вместо ряда частных критериев означает по существу решение задачи, т. к. для однокритериальных задач существует множество хорошо развитых методов (в частности, решение задачи оптимизации ). С появлением обобщенного критерия исчезают логические проблемы и остаются лишь вычислительные трудности.
В зависимости от того, каким образом выбираются и объединяются выходные параметры в скалярной функции качества, различают частные, аддитивные, мультипликативные, минимаксные, максиминные, статистические критерии и т. д.
Частные критерии могут применяться в тех случаях, когда среди выходных параметров можно выделить один основной параметр 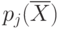 , наиболее полно отражающий эффективность проектируемого объекта. Этот параметр и принимают за целевую функцию.
, наиболее полно отражающий эффективность проектируемого объекта. Этот параметр и принимают за целевую функцию.
В этом случае задача оптимального проектирования является одно-критериальной задачей математического программирования: максимизировать (или минимизировать) значение целевой функции:
 |
( 6.6) |
при наличии системы ограничений на параметры проектируемого объекта.
Примерами таких параметров являются: мощность - для энергетического объекта, процент выхода годных - для серийно выпускаемых полупроводниковых приборов, производительность - для технологического автомата. Для многих технических объектов таким параметром служит стоимость. Условия работоспособности всех остальных выходных параметров объекта относят к функциональным ограничениям. Оптимизация на основе такой постановки называется оптимизацией по частному критерию.
Достоинством частного критерия является его простота, но имеется существенный недостаток: запас работоспособности можно получить только по тому параметру, который принят в качестве целевой функции, а другие выходные параметры вообще не будут иметь запасов.
Аддитивные критерии. В аддитивных критериях целевая функция образуется путем сложения нормированных значений частных критериев. Частные критерии имеют различную физическую природу и, следовательно, различную размерность. Поэтому сложение частных критериев возможно только после приведения их к безразмерному виду. Нормированные критерии представляют собой отношение "натурального" частного критерия к некоторой нормирующей величине, измеряемой в тех же единицах, что и сам критерий. При этом выбор нормирующего делителя должен быть логически обоснован.
Первый подход предполагает использование в качестве нормирующего делителя директивных значений параметров, заданных заказчиком. Слабым моментом такого подхода является негласное предположение о том, что в техническом задании на проектируемый объект заданы оптимальные значения параметров объекта и что совокупность заданных критериев рассматривается как образцовая.
Второй подход предполагает выбор в качестве нормирующих делителей максимальных значений критериев, достигаемых в области существования проектных решений (в области компромисса).
Возможен подход, при котором в качестве нормирующих делителей выбирают разность между максимальным и минимальным значениями критерия (в области компромисса).
Формирование безразмерной формы частных критериев в значительной мере носит субъективный характер и должно обосновываться в каждом конкретном случае.
Пусть при проектировании или серийном выпуске изделия существует I частных критериев. Тогда целевая функция задачи оптимизации при применении аддитивного критерия имеет вид
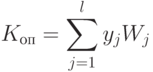 |
( 6.7) |
где 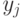 - нормированное значение частного показателя (критерия) качества;
- нормированное значение частного показателя (критерия) качества;
 - значимость соответствующего критерия качества, т. е. его весомость среди других частных критериев (весовой коэффициент). Функция (6.7) позволяет осуществлять компромисс, при котором улучшение значения одного нормированного частного критерия компенсирует ухудшение значений других.
- значимость соответствующего критерия качества, т. е. его весомость среди других частных критериев (весовой коэффициент). Функция (6.7) позволяет осуществлять компромисс, при котором улучшение значения одного нормированного частного критерия компенсирует ухудшение значений других.
Определение весовых коэффициентов 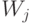 сводится либо к использованию формальных процедур, либо к применению экспертных оценок.
сводится либо к использованию формальных процедур, либо к применению экспертных оценок.
Одним из значительных недостатков аддитивного критерия, отмечаемых авторами многих работ, является то, что в нем может происходить взаимная компенсация частных критериев. Уменьшение значения одного из частных критериев вплоть до нулевого может быть покрыто за счет другого, и это не скажется на конечном результате. Для ослабления этого недостатка вводят, например, ограничение на минимальные значения частных критериев и их весовых коэффициентов.
Несмотря на недостатки аддитивного критерия, его использование помогает решать многие технические задачи.
Мультипликативные критерии.Аддитивные критерии основаны на принципе компромисса, принципе справедливой уступки, компенсации абсолютных значений нормированных частных критериев. В тех случаях, когда отсутствуют условия работоспособности типа равенств и выходные параметры не могут принимать нулевые значения, может применяться мультипликативный критерий. Последний использует не абсолютные, а относительные изменения значений частных критериев.
Принцип справедливой относительной уступки формулируется следующим образом: справедливым следует считать такой компромисс, когда суммарный уровень относительного снижения одного или нескольких критериев не превышает суммарного уровня относительного увеличения остальных критериев.
В математической форме условие оптимальности на основе принципа справедливой относительной уступки записывается в виде
 |
( 6.8) |
где 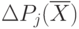 - приращение величины
- приращение величины  -го критерия;
-го критерия;
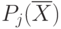 - первоначальная величина
- первоначальная величина  -го критерия.
-го критерия.
Полагая 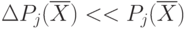 , выражение (6.8) представляют как дифференциал натурального логарифма
, выражение (6.8) представляют как дифференциал натурального логарифма
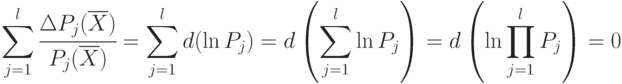 |
( 6.9) |
Ввиду монотонности логарифмической функции в условии (6.8) достигает максимального значения функция, стоящая под знаком логарифма в последнем равенстве формулы (6.9). Следовательно, принцип относительной уступки приводит к мультипликативному обобщенному критерию оптимальности:
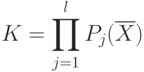 |
( 6.10) |
Мультипликативный критерий образуется путем простого перемножения частных критериев в том случае, если все они имеют одинаковую важность (весомость). Если же их весомость различна, то вместо простого перемножения мультипликативный обобщенный критерий выражается через частные критерии следующим образом:
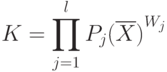 |
( 6.11) |
где обозначения приняты те же, что и ранее.
Обобщенный мультипликативный критерий не требует нормирования частных критериев, и в этом заключается его преимущество перед аддитивным критерием. Но мультипликативный критерий имеет и серьезные недостатки: критерий компенсирует недостаточную величину одного частного критерия избыточной величиной другого, а также имеет тенденцию сглаживать уровни частных критериев, поскольку в соответствии с принципом относительной уступки абсолютное изменение критерия при оптимизации тем больше, чем больше его первоначальная величина.
Максиминные (минимаксные) критерии, основанные на принципе равномерности.Сущность максимальных критериев заключается в следующем. Основываясь на идее равномерного компромисса, осуществляют
поиск такой совокупности переменных проектирования, при которой нормированные значения всех частных критериев 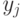 становятся равными между собой, т. е.
становятся равными между собой, т. е.
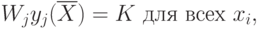 |
( 6.12) |
Поскольку при большом числе частных критериев выполнить соотношение (6.12) сложно, для решения задачи используют принцип макси-мина. Последний предполагает такую вариацию значений переменных проектирования  , при которой последовательно "подтягивают" те нормированные критерии, численные значения которых в исходном решении оказались наименьшими.
Т. к. оптимизация осуществляется в области компромисса, подтягивание "отстающего" критерия неизбежно приводит к снижению некоторых других частных критериев. Но проводя последовательно увеличение каждого "отстающего" критерия, добиваются в определенной степени уравнивания конфликтных частных критериев, что и является целью оптимизации по принципу мак-симина.
Математически принцип максимина формулируется следующим образом: найти такую совокупность
, при которой последовательно "подтягивают" те нормированные критерии, численные значения которых в исходном решении оказались наименьшими.
Т. к. оптимизация осуществляется в области компромисса, подтягивание "отстающего" критерия неизбежно приводит к снижению некоторых других частных критериев. Но проводя последовательно увеличение каждого "отстающего" критерия, добиваются в определенной степени уравнивания конфликтных частных критериев, что и является целью оптимизации по принципу мак-симина.
Математически принцип максимина формулируется следующим образом: найти такую совокупность  , при которой реализуется максимум из минимальных значений частных критериев, т. е.
, при которой реализуется максимум из минимальных значений частных критериев, т. е.
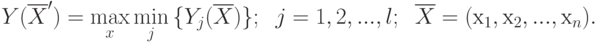 |
( 6.13) |
В случае минимаксного принципа самым "отстающим" критерием является тот, который имеет максимальное значение. В этом случае реализуется минимум из максимальных значений частных критериев:
 |
( 6.14) |
Приведенные критерии не являются единственными. Известны и иногда используются такие критерии, как статистические, детерминированные, критерии формы функции и т. д. При выборе критерия оптимальности необходимо исходить из той цели, которая преследуется при проектировании нового технического объекта. Стоимость и надежность системы, энергоемкость и производительность агрегата, показатели качества проектируемого и выпускаемого серийно прибора всегда находятся в противоречии друг с другом. Поэтому при выборе критерия следует учитывать требования, которые сформулированы в техническом задании: если в ТЗ предъявляется требование по одному выходному параметру, то следует использовать частный критерий; если же необходимо учесть все показатели качества, которые можно измерить, то следует использовать аддитивный критерий; в случае если необходимо учесть изменение абсолютных значений частных критериев, следует использовать мультипликативный критерий и т. д.
