Компоновка модулей. Методы разбиения электрических схем на функционально законченные модули
Показать на конкретном примере решение задач разбиения электрической схемы.
19.1. Общая постановка задачи
К первоочередной задаче конструирования относится компоновка узлов, т.е. распределение схемы по конструктивно-функциональным узлам.
РЭС в общем случае всегда содержит иерархию конструктивных частей (см. рис. 19.2).
Многоуровневый процесс компоновки может выполняться "снизу вверх" или "сверху вниз".
В первом случае осуществляется последовательная компоновка узлов возрастающей сложности (например: плат, панелей, стоек.), а во втором - узлы высшего уровня последовательно разбиваются на узлы меньшей сложности.
В ходе указанного процесса определяется состав каждого конструктивного узла, а также схемы внутриузловых и межузловых соединений.
Поскольку каждый узел является конструктивно неделимым элементом по отношению к узлу более высокого уровня, то его называют просто элементом.
Узлы составляют конструктивный базис устройства и, как правило, функционально унифицированы.
Среди задач компоновки узлов можно выделить два характерных класса.
К первому относятся задачи компоновки конструктивных узлов, в которых осуществляется разбиение схем на узлы с учётом таких ограничений, как количество элементов в узлах, число внешних выводов на узлах, суммарная площадь, занимаемая элементами и соединениями, и количество узлов.
Главными критериями для такого разбиения являются: минимум числа образующихся узлов, минимум числа межузловых соединений или внешних выводов на узлах.
Такие задачи возникают при разбиении схемы устройства на узлы большой степени сложности, к которым не предъявлены требования в отношении схемной унификации. Прежде всего, это задачи распределения отдельных печатных плат (ТЭЗов) по панелям в ЭВМ, распределения микросборок по печатным платам и разбиение схем на БИСы частичного применения.
Требования минимизации числа частей и количества их межсоединений остаются в силе и при разбиении схем на конструктивные единицы, содержащие функционально законченные комбинации элементов (части счётчиков, регистров, матриц памяти). В этом случае указанные функциональные образования могут рассматриваться в процессе компоновки как единое целое с соответствующими конструктивными параметрами (занимаемый объём, число внешних соединений) и далее распределяться по узлам более высокого уровня так же, как и действительные конструктивные элементы.
К отмеченным выше критериям и ограничениям могут быть добавлены и другие, например, условия, обеспечивающие электромагнитную совместимость отдельных элементов в узле и нормальный режим теплообмена. Эти условия либо должны быть выяснены до компоновки и реализованы правильным назначением критических групп элементов в соответствующие узлы, либо проверены после компоновки. В последнем случае возможно перераспределение некоторых элементов.
В ряде случаев при компоновке узлов особое внимание должно быть уделено определённым соединениям. Это, прежде всего, касается минимизации задержек в распространении сигналов. Как правило, переход соединительных цепей с одного уровня на другой влечёт за собой уменьшение быстродействия схем или необходимость введения усилительных каскадов. Поэтому при компоновке целесообразно локализовать некоторые цепи в пределах одного узла, например, цепи обратных связей в логических схемах. С другой стороны, определённые сигналы должны быть доступны для контроля неисправностей и поэтому должны иметь внешние выводы. Целесообразно может быть также создание и повторение отдельных элементов и сигналов с целью минимизации задержек или сокращения необходимого числа внешних выводов. Решение последней задачи особенно важно при реализации устройств на основе БИС, поскольку удельная стоимость одного внешнего вывода в таких схемах, измеряемая требуемой площадью реализации, становится эквивалентной стоимости десятков и сотен комп онентов. В таких ситуациях может потребоваться коррекция отдельных фрагментов или даже всей схемы в целом.
Таким образом, к первому классу задач компоновки относятся такие, в которых критерии оптимизации и ограничения могут быть сведены к определенным конструктивным параметрам расположения отдельных элементов и их межсоединений.
Их называют задачами компоновки конструктивных узлов.
Второй класс задач образуют задачи компоновки, в которых, помимо конструктивных характеристик образующихся узлов, существенны и их функциональные характеристики. Эти задачи возникают на этапе перехода от логических схем цифровых устройств к принципиально - электрическим схемам и состоят в назначении элементов логической схемы в типовые модули из заданного набора. Каждый из типовых модулей включает несколько логических элементов или их функциональных групп, в общем случае соединённых между собой. Набор типовых модулей должен обладать свойством полноты, т. е обеспечивать реализацию любой логической схемы.
Задача построения оптимального набора схемно - унифицированных модулей представляет значительные затруднения и до настоящего времени остается мало изученной. Отдельные результаты в этом направлении относятся к построению количественных оценок эффективности наборов на основании анализа результатов конкретных схем. Эти оценки характеризуют повторяемость некоторых узлов, избыточность покрытия, степень разгрузки межмодульных соединений и другие, и могут быть использованы для сравнения различных наборов.
В дальнейшем будем считать, что набор типовых модулей задан.
Основными критериями при компоновке схем типовыми модулями являются:
- минимум числа модулей, необходимых для покрытия исходной схемы;
- минимум количества межмодульных соединений;
- минимум числа типов используемых модулей;
- и другие.
В качестве ограничений принимают конструктивные и функциональные характеристики типовых модулей.
После проведения компоновки узлов электронного устройства решаются задачи размещения элементов в конструктивном объёме этих узлов и трассировки межсоединений.
19.2. Математическая формулировка задачи разбиения
Для построения формальной математической модели компоновочных задач используют теорию графов. При этом электрическую схему интерпретируют ненаправленным мультиграфом, в котором каждому конструктивному элементу (модулю) ставят в соответствие вершину мультиграфа, а электрическим связям схемы - его рёбра.
Тогда задача компоновки формулируется следующим образом.
Задан мультиграф 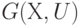 .Задача компоновки формулируется как задача разбиения или "разрезания" этого графа на отдельные куски
.Задача компоновки формулируется как задача разбиения или "разрезания" этого графа на отдельные куски 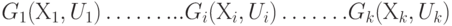 так, чтобы число рёбер, соединяющих эти куски, было минимальным, т.е. необходимо минимизировать величину
так, чтобы число рёбер, соединяющих эти куски, было минимальным, т.е. необходимо минимизировать величину
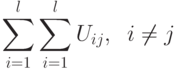 |
( 19.1) |
где 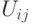 - множество ребер, соединяющих куски
- множество ребер, соединяющих куски 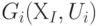 и
и  .
.
Совокупность частей 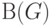 называется разбиением (разрезанием) графа
называется разбиением (разрезанием) графа  если
если
![\forall G_{ i }\in В (G) (G_{ i }\ne \varnothing ), i\in I; \\
\forall G_{i }, G_{j} \in В (G) [G_{i }\ne G_{j} \Rightarrow Х_{i}
I\limits_{i\in I}Х_{j} = \varnothing \wedge ( U_{i } I U_{j} = U_{ i j }\vee U_{i j} I U_{j} = \varnothing )];\\
\bigcup\limits_{i\in I}G_{ i }= G.](/sites/default/files/tex_cache/4ec3ece15def51a5d09957914635717e.png) |
( 19.2) |
Другими словами, совокупность 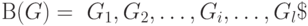 является разбиением графа
является разбиением графа  если любая из этой совокупности не пустая, если для любых двух частей из
если любая из этой совокупности не пустая, если для любых двух частей из 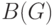 пересечение множества вершин пусто, а пересечение множества ребер может быть не пустым, а также, если объединение всех частей в точности равно графу
пересечение множества вершин пусто, а пересечение множества ребер может быть не пустым, а также, если объединение всех частей в точности равно графу  .
.
В выражении (19.2) U_{ i j} определяет подмножество рёбер 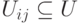 , попадающих в разрез (сечение) между частями
, попадающих в разрез (сечение) между частями 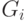 и
и 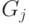 графа
графа  .
.
Задачей разбиения графа  является нахождение такой совокупности частей,
при которой число рёберного соединения графа
является нахождение такой совокупности частей,
при которой число рёберного соединения графа  удовлетворяло бы заданному критерию оптимальности.
удовлетворяло бы заданному критерию оптимальности.
В соответствии с этим разбиением множество рёбер  графа
графа  можно представит в виде:
можно представит в виде:
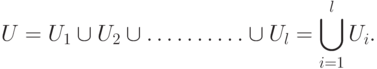 |
( 19.3) |
Тогда каждое подмножество ^{ } 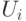 можно представить как:
можно представить как:
 |
( 19.4) |
где  - подмножество всех рёбер, инцидентных вершинам
- подмножество всех рёбер, инцидентных вершинам 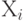 части
графа
части
графа 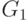 ;
; 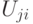 - подмножество рёбер,
соединяющих подмножество вершин
- подмножество рёбер,
соединяющих подмножество вершин 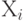 внутри
внутри 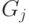 - между собой;
- между собой; 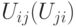 - подмножество рёбер, соединяющих части
- подмножество рёбер, соединяющих части 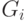 и
и 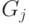 между собой.
между собой.
Отношение суммарного числа внутренних рёбер (рёбер подмножеств U_{i i}) к суммарному числу соединяющих рёбер (рёбер подмножеств 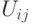 ) называется коэффициентом разбиения
) называется коэффициентом разбиения  :
:
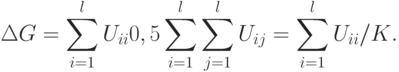 |
( 19.) |
Коэффициент разбиения 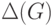 служит для оценки разбиения графа
служит для оценки разбиения графа  на части. Его можно также использовать для сравнения разбиения графов.
на части. Его можно также использовать для сравнения разбиения графов.
Под оптимальным разбиением графа 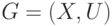 понимают такое разбиение
понимают такое разбиение 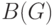 ,
при котором выполняется условие
,
при котором выполняется условие
 |
( 19.6) |
т. е. критерием оптимальности является минимальное число рёбер, соединяющих части графа между собой.

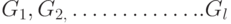 .
.