Математические модели (ММ) на различных иерархических уровнях
Назначение лекции - показать основу, базу современного подхода к проектированию РЭС, дать более глубокие сведения о математических моделях, используемых при проектировании РЭС.
13.1. Иерархия математических моделей в САПР
Блочно-иерархический подход к проектированию радиоэлектронных средств (РЭС) основан, как было сказано, на иерархии математических моделей. Деление моделей по иерархическим уровням (уровням абстрагирования) происходит по степени детализации описываемых свойств и процессов, протекающих в объекте. При этом на каждом иерархическом уровне используют свои понятия "система" и "элементы". Так, система k-го уровня рассматривается как элемент на соседнем более высоком  -м уровне абстрагирования.
-м уровне абстрагирования.
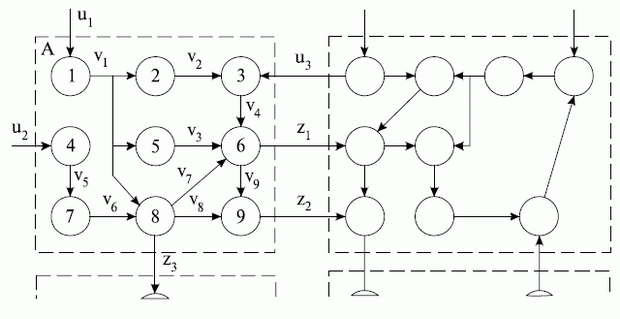
Представим структуру некоторого объекта в виде множества элементов (рис. 13.1) и связей между ними.
Выделим в соответствии с блочно-иерархическим подходом в структуре объекта некоторые подмножества элементов и назовем их блоками (на рисунке показаны штриховыми линиями). Пусть состояние каждой связи характеризуется одной фазовой переменной 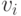 ,
, 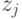 или
или  .
Здесь
.
Здесь 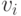 относится к внутренним связям между элементами данного блока,
относится к внутренним связям между элементами данного блока, 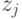 и
и  относятся к выходам и входам блока, соответственно. Рассмотрим важные для функциональных моделей понятия полной модели и макромодели.
относятся к выходам и входам блока, соответственно. Рассмотрим важные для функциональных моделей понятия полной модели и макромодели.
Полная модель блока есть модель, составленная из моделей элементов с учетом межэлементных связей, т. е. модель, описывающая как состояние выходов, так и состояние каждого из элементов блока. Моделями элементов блока А являются уравнения, связывающие входные и выходные переменные:
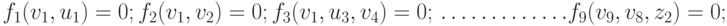 |
( 13.1) |
Полная модель блока есть система уравнений
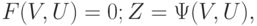 |
( 13.2) |
где  ,
,  и
и  - векторы внутренних, выходных и входных фазовых переменных блока.
- векторы внутренних, выходных и входных фазовых переменных блока.
При большом количестве элементов размерность вектора  и порядок системы уравнений (13.1) становятся чрезмерно большими и требуют упрощения.
и порядок системы уравнений (13.1) становятся чрезмерно большими и требуют упрощения.
При переходе к более высокому иерархическому уровню упрощения модели основаны на исключении из модели вектора внутренних переменных  .
Полученная модель представляет собой систему уравнений
.
Полученная модель представляет собой систему уравнений
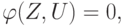 |
( 13.3) |
существенно меньшей размерности, чем полная модель (13.2), и называется макромоделью. Следовательно, макромодель уже не описывает процессы внутри блока, а характеризует только процессы взаимодействия данного блока с другими в составе системы блоков.
Модели (13.2) и (13.3) относятся друг к другу как полная модель и макромодель на  -м уровне иерархии. На более высоком
-м уровне иерархии. На более высоком  уровне блок А рассматривается как элемент, и макромодель (13.3) становится моделью элемента А. Следовательно, модели (13.1) и (13.3) относятся друг к другу как модели элементов соседних иерархических уровней. Из моделей типа (13.3) может быть составлена полная модель системы на
уровне блок А рассматривается как элемент, и макромодель (13.3) становится моделью элемента А. Следовательно, модели (13.1) и (13.3) относятся друг к другу как модели элементов соседних иерархических уровней. Из моделей типа (13.3) может быть составлена полная модель системы на  -м уровне.
-м уровне.
13.2. Микро-, макро- и метауровни
В зависимости от сложности объекта при его проектировании используют большее или меньшее число уровней абстракции. Объединение уровней, родственных по характеру используемого математического аппарата, приводит к образованию в иерархии функциональных моделей для большинства проектируемых сложных объектов трех укрупненных уровней: микро-, макро- и метауровней.
На микроуровне используют математические модели, описывающие физическое состояние и процессы в сплошных средах. Для моделирования применяют аппарат уравнений математической физики. Примерами таких уравнений служат дифференциальные уравнения в частных производных - уравнения электродинамики, теплопроводности, упругости, газовой динамики. Эти уравнения описывают поля электрического потенциала и температуры в полупроводниковых кристаллах интегральных схем. К типичным фазовым переменным на микроуровне относятся электрические потенциалы, давление, температура, концентрации частиц, плотности токов. Независимыми переменными являются время и пространственные координаты. В качестве операторов  и
и  в уравнениях (13.2) фигурируют дифференциальные и интегральные операторы. Уравнения (13.2), дополненные краевыми условиями, составляют ММ объектов на микроуровне. Анализ таких моделей сводится к решению краевых задач математической физики.
в уравнениях (13.2) фигурируют дифференциальные и интегральные операторы. Уравнения (13.2), дополненные краевыми условиями, составляют ММ объектов на микроуровне. Анализ таких моделей сводится к решению краевых задач математической физики.
На макроуровне производится дискретизация пространств с выделением в качестве элементов отдельных деталей, дискретных электрорадиоэлементов, участков полупроводниковых кристаллов. При этом из числа независимых переменных исключают пространственные координаты. Функциональные модели на макроуровне представляют собой системы алгебраических или обыкновенных дифференциальных уравнений. Для их получения и решения используют соответствующие численные методы. В качестве фазовых переменных фигурируют электрические напряжения, токи, силы, скорости, температуры, расходы и т. д. Они характеризуют проявления внешних свойств элементов при их взаимодействии между собой и внешней средой в электронных схемах или механических конструкциях.
На метауровне с помощью дальнейшего абстрагирования от характера физических процессов удается получить приемлемое по сложности описание информационных процессов, протекающих в проектируемых объектах. На метауровне для моделирования аналоговой РЭС широко применяют аппарат анализа систем автоматического управления, а для моделирования цифровой РЭС - математическую логику, теорию конечных автоматов, теорию массового обслуживания. Математические модели на метауровне - системы обыкновенных дифференциальных уравнений, системы логических уравнений, имитационные модели систем массового обслуживания.
Математические модели на микроуровне
Модели на микроуровне используются для исследования напряженного состояния деталей конструкции и для расчетов их на прочность.
Напряженное состояние деталей конструкции в зависимости от геометрии исследуемого узла, вида приложенной нагрузки и свойств материала описывается дифференциальными уравнениями различного вида. Любое из этих уравнений может быть получено из общего квазигармонического уравнения
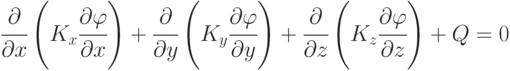 |
( 13.4) |
где  ,
,  ,
,  - пространственные координаты;
- пространственные координаты;  - искомая непрерывная функция;
- искомая непрерывная функция;  ,
,  ,
, 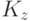 - коэффициенты;
- коэффициенты;  - внешнее воздействие.
- внешнее воздействие.
Точное решение краевых задач получают только в частных случаях. Поэтому реализация таких моделей заключается в использовании различных приближенных моделей. Широкое распространение получили модели на основе интегральных уравнений и модели на основе метода сеток. Одним из наиболее популярных методов решения краевых задач в САПР является метод конечных элементов.
Математические модели на макроуровне
Большинство технических подсистем характеризуется фазовыми переменными. Фазовые переменные образуют вектор неизвестных в ММ технической системы. Для каждой физической подсистемы характерны свои законы, однако для простейших элементов форма выражающих их уравнений оказывается одинаковой. Ниже приводится в качестве примера электрическая подсистема.
Электрическая подсистема
Фазовыми переменными электрической подсистемы являются токи I и напряжения U. Запишем уравнения трех типов простейших элементов.
- Уравнение сопротивления (закон Ома)
 , где
, где 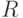 - электрическое сопротивление.
- электрическое сопротивление. - Уравнение емкости
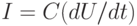 , где
, где  - электрическая емкость.
- электрическая емкость. - Уравнение индуктивности
 , где
, где  - электрическая индуктивность.
- электрическая индуктивность.
Математические модели на метауровне
Математические модели в технологических системах довольно разнообразны.
Математические модели с использованием целочисленного программирования
Для создания технологических структур из РТК необходимо приобрести n PTK для участка. Для этого выделен фонд в сумме  рублей. Стоимость РТК
рублей. Стоимость РТК  -гo типа
-гo типа 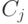 , а производительность
, а производительность 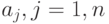 . Требуется выбрать РТК, обеспечивающие максимальную суммарную производительность в пределах установленного денежного лимита
. Требуется выбрать РТК, обеспечивающие максимальную суммарную производительность в пределах установленного денежного лимита  . Математическая модель:
. Математическая модель:
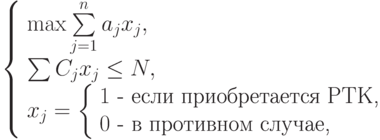 |
( 13.5) |
где 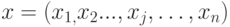 ;
;  ;
;  ;
;  - целые числа.
- целые числа.
Решение ведется методом ветвей и границ.
Если отбросить требования целочисленности, переменные 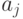 ,
, 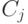 изменяются непрерывно на отрезке
изменяются непрерывно на отрезке ![[0, 1]](/sites/default/files/tex_cache/264884439b70ab09a86bc848421c6de6.png) . Решение такой непрерывной задачи будет верхней границей (так как определяется максимум) множества значений целевой функции на соответствующем подмножестве решения. Алгоритм решения непрерывной задачи состоит в следующем. Упорядочим коэффициенты
. Решение такой непрерывной задачи будет верхней границей (так как определяется максимум) множества значений целевой функции на соответствующем подмножестве решения. Алгоритм решения непрерывной задачи состоит в следующем. Упорядочим коэффициенты 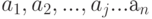 в порядке убывания величин
в порядке убывания величин  и соответственно этому порядку пронумеруем переменные и параметры задачи.
и соответственно этому порядку пронумеруем переменные и параметры задачи.
Процедура разбиения (методом ветвей и границ) допустимого множества  , задаваемого ограничениями, такова. Разбивают
, задаваемого ограничениями, такова. Разбивают 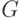 на два подмножества
на два подмножества 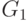 и
и 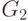 . Первому подмножеству принадлежат все решения с
. Первому подмножеству принадлежат все решения с 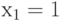 , а второму - с
, а второму - с  . Далее каждое из подмножеств
. Далее каждое из подмножеств  и
и 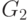 опять разбивают на два: в первом
опять разбивают на два: в первом 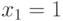 , во втором
, во втором 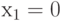 и т. д.
и т. д.
На каждом шаге очередного разбиения выбирают подмножество, которому соответствует максимальное значение оценки. Поиск решения заканчивают, если на некотором шаге получают допустимое решение значения целевой функции, на котором шаг будет наибольшим по сравнению с оценками для всех подмножеств - кандидатов на разбиение.
Математические модели с использованием систем массового обслуживания
Эти системы основаны на марковском случайном процессе. Физическая система  с течением времени меняет свое состояние (переходит из одного состояния в другое) случайным образом. Тогда в системе
с течением времени меняет свое состояние (переходит из одного состояния в другое) случайным образом. Тогда в системе  протекает случайный процесс, который называется марковским, если для любого момента времени
протекает случайный процесс, который называется марковским, если для любого момента времени  вероятностные характеристики процесса в "будущем" зависят только от его состояния в данный момент времени
вероятностные характеристики процесса в "будущем" зависят только от его состояния в данный момент времени  и не зависят от того, когда и как система пришла в это состояние. Вероятностные характеристики в "будущем" можно найти: например, вероятность того, что через некоторое время т система
и не зависят от того, когда и как система пришла в это состояние. Вероятностные характеристики в "будущем" можно найти: например, вероятность того, что через некоторое время т система  окажется в состоянии
окажется в состоянии 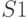 или сохранит состояние
или сохранит состояние 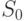 , и т. д.
, и т. д.
Таким образом, в марковском случайном процессе "будущее" зависит от "прошлого" только через "настоящее".
Рассматривая марковские процессы с дискретными состояниями и непрерывным временем, удобно будет представлять, что все переходы системы 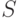 из состояния в состояние происходят под действием каких-то потоков событий (поток вызовов, отказов, восстановлений и т. п.). Если все потоки событий, переводящие систему
из состояния в состояние происходят под действием каких-то потоков событий (поток вызовов, отказов, восстановлений и т. п.). Если все потоки событий, переводящие систему 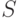 из состояния в состояние, - простейшие, то процесс, протекающий в системе, будет марковским. Это и естественно, так как простейший поток не обладает последействием: в нем "будущее" не зависит от "прошлого".
из состояния в состояние, - простейшие, то процесс, протекающий в системе, будет марковским. Это и естественно, так как простейший поток не обладает последействием: в нем "будущее" не зависит от "прошлого".
Если система S находится в каком-то состоянии 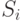 , из которого есть непосредственный переход в другое состояние
, из которого есть непосредственный переход в другое состояние 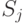 (стрелка, ведущая из
(стрелка, ведущая из 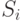 в
в 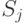 на графе состояний), то это можно представлять так, как будто на систему, пока она находится в состоянии
на графе состояний), то это можно представлять так, как будто на систему, пока она находится в состоянии 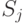 , действует простейший поток событий, приводящий ее по стрелке
, действует простейший поток событий, приводящий ее по стрелке  . Как только появится первое событие этого потока, происходит "перескок" системы из
. Как только появится первое событие этого потока, происходит "перескок" системы из 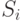 в
в 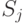 .
.
Для наглядности очень удобно представлять граф состояний. Построим размеченный граф состояний для технического устройства из двух узлов. Состояния системы будут:
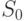 - оба узла исправны;
- оба узла исправны;
 - первый узел ремонтируется, второй исправен;
- первый узел ремонтируется, второй исправен;
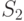 - второй узел ремонтируется, первый исправен;
- второй узел ремонтируется, первый исправен;
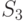 - оба узла ремонтируются.
- оба узла ремонтируются.
Интенсивность потоков событий, переводящих систему из состояния в состояние, вычисляется при условии, что среднее время ремонта узла не зависит от того, ремонтируется ли один узел или оба сразу.
Это будет именно так, если ремонтом каждого узла занят отдельный специалист.
Найдем все интенсивности потоков событий, переводящих систему из состояния в состояние.
Пусть система находится в состоянии 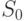 . Какой поток событий переводит ее в состояние
. Какой поток событий переводит ее в состояние  ? Очевидно, поток отказов первого узла.
Его интенсивность
? Очевидно, поток отказов первого узла.
Его интенсивность 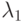 равна единице, деленной на среднее время безотказной работы первого узла.
Какой поток событий переводит систему обратно из
равна единице, деленной на среднее время безотказной работы первого узла.
Какой поток событий переводит систему обратно из 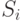 в
в 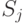 ?
Очевидно, поток "окончаний ремонтов" первого узла.
Его интенсивность
?
Очевидно, поток "окончаний ремонтов" первого узла.
Его интенсивность 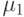 равна единице, деленной на среднее время ремонта первого узла. Аналогично вычисляются интенсивности потоков событий, переводящих систему по всем стрелкам графа рис. 13.2.
равна единице, деленной на среднее время ремонта первого узла. Аналогично вычисляются интенсивности потоков событий, переводящих систему по всем стрелкам графа рис. 13.2.
Имея в своем распоряжении размеченный граф состояний системы, легко построить математическую модель данного процесса.
В самом деле, пусть рассматривается система  , имеющая
, имеющая  возможных состояний
возможных состояний 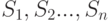 . Назовем вероятностью i-го состояния вероятность
. Назовем вероятностью i-го состояния вероятность  того, что в момент
того, что в момент  система будет находиться в состоянии
система будет находиться в состоянии 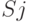 . Очевидно, что для любого момента сумма всех вероятностей состояний равна единице:
. Очевидно, что для любого момента сумма всех вероятностей состояний равна единице:
 |
( 13.6) |
Имея в своем распоряжении размеченный граф состояний, можно найти все вероятности состояний  как функции времени. Для этого составляют и решают так называемые уравнения Колмогорова - особый вид дифференциальных уравнений, в которых неизвестными функциями являются вероятности состояний.
как функции времени. Для этого составляют и решают так называемые уравнения Колмогорова - особый вид дифференциальных уравнений, в которых неизвестными функциями являются вероятности состояний.