Микропроцессорные системы и способы распараллеливания
Способы распараллеливания
Различают два основных способа распараллеливания: по управлению и по информации.
Первый способ — представление алгоритма задачи в виде частично-упорядоченной последовательности выполняемых работ. Затем в результате диспетчирования реализуется оптимальный план выполнения работ в ВС при ограничениях на время выполнения всего алгоритма или за минимальное время.
Основой является представление алгоритма граф-схемой G, отражающей информационные связи между работами (задачами, процессами, процедурами, операторами, макрокомандами и т.д.), на которые разбит алгоритм. Граф G — взвешенный, ориентированный, без контуров.
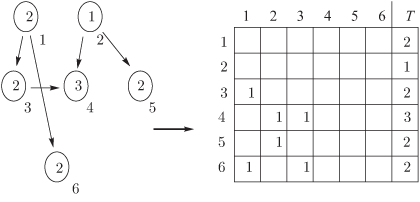
Для исследования графа и диспетчирования используют матрицы следования S ; их дополняют столбцом T весов — получают расширенные матрицы следования S* (рис. 2.4).
Здесь предполагаем, что ВС — однородная, с общей (разделяемой) памятью, т.е. потерями времени на обмен между работами можно пренебречь.
Пусть ВС содержит два процессора (n = 2). Тогда в результате оптимального распределения получим план (рис. 2.5).
План действительно совпадает с оптимальным, т.к. длина расписания T = 7, что совпадает с длиной критического пути в графе, Tкр = 7 (путь 1 -> 3 -> 4 ).
В общей схеме организации параллельного вычислительного процесса мы не полностью раскрыли содержание блока 3 — интерпретации потока макроинструкций в виде, удобном для работы диспетчера. Сейчас мы определили, что такой вид — это матрица следования. Значит, в случае необходимости автоматического формирования матрицы следования надо определять информационную взаимосвязь макроинструкций в пределах видимости, т.е. в "окне просмотра". Таким образом, по текущему содержимому "окна просмотра" надо формировать текущий вид матрицы следования.
Вспомним, что мы уже в упрощенном виде решали подобную задачу, например, когда по формируемому потоку трехадресных команд определяли их информационную взаимосвязь и определяли возможность одновременного выполнения этих команд.
Обобщим эту задачу.
Возвращаясь к названной схеме, представим себе, что поток макроинструкций
(блок 2) следует через "окно просмотра" так, что для планирования
оптимальной загрузки процессоров диспетчер может анализировать некоторое
множество этих макроинструкций и из них выбирать вариант назначения их на
процессоры для выполнения. Каждая макроинструкция может интерпретироваться
и как процедура, где можно выделить имя 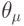 , множество
, множество 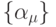 входных параметров, множество
входных параметров, множество 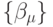 выходных параметров. На
рис. 2.6 отображено "окно просмотра", через которое следует поток
макроинструкций.
выходных параметров. На
рис. 2.6 отображено "окно просмотра", через которое следует поток
макроинструкций.
Составим по его содержимому соответствующую матрицу следования размерности m x m:

По матрице следования S диспетчер производит назначение.
После выполнения макроинструкций они исключаются из "окна прросмотра", оставшиеся макроинструкции уплотняются вверх, а снизу "окно просмотра" пополняется новыми макроинструкциями. С учетом вновь поступивших макроинструкций уточняется текущий вид матрицы следования S и процесс диспетчирования продолжается.
По такой же схеме, а именно, на основе первого способа распараллеливания — по управлению — решается другая важная задача распараллеливания: компоновки длинных командных слов в оптимизирующем трансляторе. Назначение работы на ИУ осуществляется здесь в виде записи соответствующей инструкции в позицию длинного командного слова, соответствующую ИУ. Т.е. план параллельного выполнения работ (команд, операций) фиксируется в длинных командных словах, в которых предусмотрены инструкции каждому ИУ, которые они должны начать выполнять с данного такта.