|
С помощью обобщенного алгоритма Евклида найдите числа х и у, удовлетворяющие уравнению 30х +12y = НОД(30,12). х=1, у=-2, НОД = 6. Где ошибка? |
Электронная цифровая подпись
Цель лекции: познакомиться с некоторыми алгоритмами формирования и проверки электронной цифровой подписи (ЭЦП, ЭП).
Электронная подпись на основе алгоритма RSA
Рассмотренная нами в Лекции 11 схема использования алгоритма RSA при большом модуле N практически не позволяет злоумышленнику получить закрытый ключ и прочитать зашифрованное сообщение. Однако она дает возможность злоумышленнику подменить сообщение от абонента А к абоненту Б, так как абонент А шифрует свое сообщение открытым ключом, полученным от Б по открытому каналу связи. А раз открытый ключ передается по открытому каналу, любой может получить его и использовать для подмены сообщения. Избежать этого можно, используя более сложные протоколы, например, следующий.
Пусть, как и раньше, пользователь А хочет передать пользователю Б сообщение, состоящее из нескольких блоков mi. Перед началом сеанса связи абоненты генерируют открытые и закрытые ключи, обозначаемые, как указано в следующей таблице:
В результате каждый пользователь имеет свои собственные открытый (состоящий из двух частей) и закрытый ключи. Затем пользователи обмениваются открытыми ключами. Это подготовительный этап протокола.
Основная часть протокола состоит из следующих шагов.
- Сначала пользователь А вычисляет числа
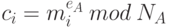 , то есть шифрует сообщение своим закрытым ключом. В результате этих действий пользователь А подписывает сообщение.
, то есть шифрует сообщение своим закрытым ключом. В результате этих действий пользователь А подписывает сообщение. - Затем пользователь А вычисляет числа
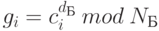 , то есть шифрует то, что получилось на шаге 1 открытым ключом пользователя Б. На этом этапе сообщение шифруется, чтобы никто посторонний не мог его прочитать.
, то есть шифрует то, что получилось на шаге 1 открытым ключом пользователя Б. На этом этапе сообщение шифруется, чтобы никто посторонний не мог его прочитать. - Последовательность чисел gi передается к пользователю Б.
- Пользователь Б получает gi и вначале вычисляет последовательно числа
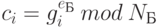 , используя свой закрытый ключ. При этом сообщение расшифровывается.
, используя свой закрытый ключ. При этом сообщение расшифровывается. - Затем Б определяет числа
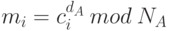 , используя открытый ключ пользователя А.
За счет выполнения этого этапа производится проверка подписи пользователя А.
, используя открытый ключ пользователя А.
За счет выполнения этого этапа производится проверка подписи пользователя А.
В результате абонент Б получает исходное сообщение и убеждается в том, что его отправил именно абонент А. Данная схема позволяет защититься от нескольких видов возможных нарушений, а именно:
- пользователь А не может отказаться от своего сообщения, если он признает, что секретный ключ известен только ему;
- нарушитель без знания секретного ключа не может ни сформировать, ни сделать осмысленное изменение сообщения, передаваемого по линии связи.
Данная схема позволяет избежать многих конфликтных ситуаций. Иногда нет необходимости зашифровывать передаваемое сообщение, но нужно его скрепить электронной подписью. В этом случае из приведенного выше протокола исключаются шаги 2 и 4, то есть текст шифруется закрытым ключом отправителя, и полученная последовательность присоединяется к документу. Получатель с помощью открытого ключа отправителя расшифровывает прикрепленную подпись, которая, по сути, является зашифрованным повторением основного сообщения. Если расшифрованная подпись совпадает с основным текстом, значит, подпись верна.
Существуют и другие варианты применения алгоритма RSA для формирования ЭЦП. Например, можно шифровать (то есть подписывать) открытым ключом не само сообщение, а хеш-код от него.
Возможность применения алгоритма RSA для получения электронной подписи связана с тем, что секретный и открытый ключи в этой системе равноправны. Каждый из ключей, d или e, могут использоваться как для шифрования, так и для расшифрования. Это свойство выполняется не во всех криптосистемах с открытым ключом.
Алгоритм RSA можно использовать также и для обмена ключами.
Цифровая подпись на основе алгоритма Эль-Гамаля
Принцип создания и проверки подписи
Алгоритм Эль-Гамаля также можно использовать для формирования цифровой подписи. Группа пользователей выбирает общие параметры Р и А. Затем каждый абонент группы выбирает свое секретное число Хi, 1 < Хi< Р-1, и вычисляет соответствующее ему открытое число 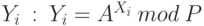 . Таким образом, каждый пользователь получает пару (закрытый ключ; открытый ключ) = (Хi, Yi). Открытые ключи пользователей могут храниться в общей базе системы распределения ключей и при необходимости предоставляться всем абонентам системы.
. Таким образом, каждый пользователь получает пару (закрытый ключ; открытый ключ) = (Хi, Yi). Открытые ключи пользователей могут храниться в общей базе системы распределения ключей и при необходимости предоставляться всем абонентам системы.
Сообщение, предназначенное для подписи, должно быть представлено в виде числа, меньшего модуля Р. При большом размере сообщение разбивается на блоки необходимого размера. В некоторых случаях подписывается не само сообщение, а значение хеш-функции от него. В любом варианте цифровая подпись вычисляется в зависимости от некоторого числа m (m < P).
Пусть пользователь 1 хочет подписать свое сообщение цифровой подписью и передать его пользователю 2. В этом случае алгоритм действий следующий.
- Первый пользователь выбирает случайное секретное число k, взаимно простое с Р-1, и вычисляет число

- Затем с помощью расширенного алгоритма Евклида необходимо найти значение b в следующем уравнении:Пара чисел (a, b) будет цифровой подписью сообщения m.
m = (X1 * a +k * b) mod (P-1)
- Сообщение m вместе с подписью (a, b) отправляется пользователю 2.
- Пользователь 2 получает сообщение m и с использованием открытого ключа первого абонента Y1 вычисляет два числа по следующим формулам:
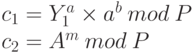 Если с1 = с2, то цифровая подпись первого пользователя верная. Для подписывания каждого нового сообщения должно каждый раз выбираться новое значение k.
Если с1 = с2, то цифровая подпись первого пользователя верная. Для подписывания каждого нового сообщения должно каждый раз выбираться новое значение k.
Подписи, созданные с использованием алгоритма Эль-Гамаля, называются рандомизированными, так как для одного и того же сообщения с использованием одного и того же закрытого ключа каждый раз будут создаваться разные подписи (a,b), поскольку каждый раз будет использоваться новое значение k. Подписи, созданные с применением алгоритма RSA, называются детерминированными, так как для одного и того же сообщения с использованием одного и того же закрытого ключа каждый раз будет создаваться одна и та же подпись.
Пример вычисления и проверки цифровой подписи
Пусть абоненты, обменивающиеся через Интернет зашифрованными сообщениями, имеют следующие общие параметры: Р = 11, А = 7.
Один из пользователей этой системы связи хочет подписать свое сообщение m=5 цифровой подписью, сформированной по алгоритму Эль-Гамаля. Вначале он должен выбрать себе закрытый ключ, например, Х1=3 и сформировать открытый ключ Y1 = 73 mod 11 = 2. Открытый ключ может быть передан всем заинтересованным абонентам или помещен в базу данных открытых ключей системы связи.
Затем пользователь выбирает случайное секретное число k, взаимно простое с Р-1. Пусть k=9 ( 9 не имеет общих делителей с 10 ). Далее необходимо вычислить число

После этого с помощью расширенного алгоритма Евклида находится значение b в уравнении:

Решением последнего уравнения будет значение b=9.
Таким образом, пара чисел (8, 9) будет цифровой подписью сообщения m=5.
Если любой другой пользователь сети желает проверить цифровую подпись в сообщении, он должен получить из базы данных открытый ключ первого пользователя (он равен 2 ), вычислить два числа с1 и с2 и сравнить их.

Так как с1 = с2, то цифровая подпись первого пользователя в сообщения m=5 верная.
