|
С помощью обобщенного алгоритма Евклида найдите числа х и у, удовлетворяющие уравнению 30х +12y = НОД(30,12). х=1, у=-2, НОД = 6. Где ошибка? |
Введение в криптографию с открытым ключом
Цель лекции: первоначальное знакомство с принципами шифрования с открытым ключом.
Предпосылки создания методов шифрования с открытым ключом и основные определения
При использовании шифрования с закрытым ключом возникают две достаточно серьезные проблемы. Первая проблема заключается в изготовлении секретных ключей и доставке их участникам информационного обмена. При большом количестве и территориальной распределенности участников информационного обмена, использующих каналы связи общего назначения, например, обычную или электронную почту, часто бывает сложно гарантировать безопасность доставки такого ключа и его подлинность. В "Поточные шифры и генераторы псевдослучайных чисел. Часть 2" учебного пособия проблема распределения ключей для симметричного шифрования была подробно рассмотрена.
Второй проблемой является обеспечение подлинности партнеров при электронном общении. Развитие деловой переписки и электронной коммерции требует наличия методов, при использовании которых невозможно было бы подменить кого-либо из участников обмена. Получатель корреспонденции должен иметь возможность удостовериться в подлинности документа, а создатель электронного послания должен быть в состоянии доказать свое авторство получателю или третьей стороне. Следовательно, электронные документы должны иметь аналог обычной подписи.
Многие криптографы работали над решением этих проблем, в результате чего во второй половине семидесятых годов ХХ века были разработаны принципиально новые подходы, позволяющие решить перечисленные выше (и некоторые другие) задачи. Основой послужило открытие так называемых асимметричных криптоалгоритмов, или методов, в которых процедуры прямого и обратного криптопреобразования выполняются на различных ключах и не имеют между собой очевидных и легко прослеживаемых связей, которые позволили бы по одному ключу определить другой. Асимметричные алгоритмы гораздо больше основаны на свойствах математических функций, чем алгоритмы симметричного шифрования, использующие в основном только операции перестановки и замены. Большой вклад в эти исследования внесли американские ученые У. Диффи (W. Diffie), Э. Хеллман (M. Hellman), Р. Меркль (R. Merkle). Они первыми предложили способы решения обеих задач, которые радикально отличаются от всех предыдущих подходов к шифрованию.
Асимметричные алгоритмы шифрования называются также алгоритмами с открытым ключом. В отличие от алгоритмов симметричного шифрования (алгоритмов шифрования с закрытым ключом), в которых для шифрования и расшифрования используется один и тот же ключ, в ассиметричных алгоритмах один ключ используется для шифрования, а другой, отличный от первого, – для расшифрования. Алгоритмы называются асимметричными, так как ключи шифрования и расшифрования разные, следовательно, отсутствует симметрия основных криптографических процессов. Один из двух ключей является открытым (public key) и может быть объявлен всем, а второй – закрытым (private key) и должен держаться в секрете. Какой из ключей, открытый или закрытый, используется для шифрования, а какой для расшифрования, определяется назначением криптографической системы.
В настоящее время асимметричные алгоритмы широко применяются на практике, например, для обеспечения информационной безопасности телекоммуникационных сетей, в том числе сетей, имеющих сложную топологию; для обеспечения информационной безопасности в глобальной сети Internet; в различных банковских и платежных системах (в том числе использующих интеллектуальные карты).
Алгоритмы шифрования с открытым ключом можно использовать для решения, как минимум, трех задач:
- Для шифрования передаваемых и хранимых данных в целях их защиты от несанкционированного доступа.
- Для формирования цифровой подписи под электронными документами.
- Для распределения секретных ключей, используемых потом при шифровании документов симметричными методами.
Односторонние функции
Все алгоритмы шифрования с открытым ключом основаны на использовании так называемых односторонних функций. Односторонней функцией (one-way function) называется математическая функция, которую относительно легко вычислить, но трудно найти по значению функции соответствующее значение аргумента. То есть, зная х легко вычислить f(x), но по известному f(x) трудно найти подходящее значение x. Под словом "трудно вычислить" понимают, что для этого потребуется не один год расчетов с использованием ЭВМ. Односторонние функции применяются в криптографии также в качестве хеш-функций (см. "Криптографические хеш-функции" ). Использовать односторонние функции для шифрования сообщений с целью их защиты не имеет смысла, так как обратно расшифровать зашифрованное сообщение уже не получится. Для целей шифрования используются специальные односторонние функции – односторонние функции с люком (или с секретом) – это особый вид односторонних функций, имеющих некоторый секрет (люк), позволяющий относительно быстро вычислить обратное значение функции.
Для односторонней функции с люком f справедливы следующие утверждения:
- зная х, легко вычислить f(x),
- по известному значению f(x) трудно найти x,
- зная дополнительно некоторую секретную информацию, можно легко вычислить x.
Использование асимметричных алгоритмов для шифрования
В 70-х годах ХХ века Диффи и Хеллман предложили принцип шифрования, основанный на использовании двух разных ключей, хотя и связанных между собой, но устроенных так, что вычислить по одному из них (открытому) другой (закрытый) практически невозможно. Этот принцип может быть использован для решения проблемы снабжения пользователей ключами шифрования/расшифрования, а точнее – для устранения этой проблемы. Согласно Диффи и Хеллману предварительно распределяемые закрытые ключи вообще не должны использоваться для шифрования данных (так как секрет, который известен более чем одному человеку, – уже не секрет). Закрытый ключ должен быть известен только одному лицу – его владельцу. Такой принцип использования асимметричных алгоритмов получил название открытого шифрования или шифрованием с открытым ключом.
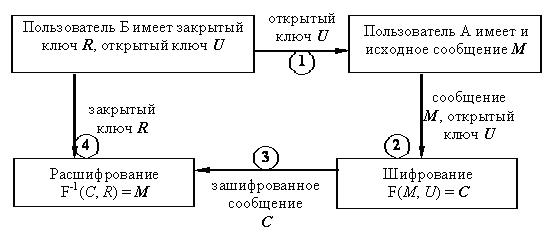
Согласно этому принципу, любой желающий может зашифровать сообщение открытым ключом. Расшифровать сообщение сможет только владелец закрытого ключа. Пусть, например, пользователи А и Б, имеющие возможность обмениваться электронными сообщениями, используют схему открытого шифрования. Предположим, пользователь А должен передать секретное сообщение пользователю Б так, чтобы никто другой не смог его прочитать. Для этого необходимо выполнить следующие действия:
- Пользователь Б посылает пользователю А свой открытый ключ U по любому каналу связи, например, по электронной почте.
- Пользователь А шифрует свое сообщение М полученным открытым ключом U и получает зашифрованное сообщение С.
- Зашифрованное сообщение С пересылается пользователю Б.
- Пользователь Б расшифровывает полученное сообщение С своим закрытым ключом R.
Если операцию шифрования обозначить как F, а операцию расшифрования как F-1, то схему протокола обмена информацией между пользователями можно изобразить, как на рис. 9.1.
Использование открытого шифрования снимает проблему распределения ключей. Раньше пользователи перед обменом зашифрованными данными должны были каким-либо образом по закрытому каналу связи согласовывать используемый секретный ключ. Для этого они могли встретиться лично или использовать курьера. Если один из пользователей считал нужный изменить ключ, он должен был передать новый ключ своему абоненту. Криптография с открытыми ключами все упрощает. Теперь абоненты не должны заботиться о возможности компрометации секретного ключа. Пользователи системы связи могут совершенно свободно обмениваться открытыми ключами и зашифрованными ими сообщениями. Если пользователь надежно хранит свой закрытый ключ, никто не сможет прочитать передаваемые сообщения.
Для упрощения процедуры обмена в сети передачи сообщений обычно используется база данных (подробнее об этом см. в "Криптографические алгоритмы с открытым ключом и их использование" ), в которой хранятся открытые ключи всех пользователей. При необходимости любой пользователь системы может запросить из базы открытый ключ другого человека и использовать полученный ключ для шифрования сообщений.