|
С помощью обобщенного алгоритма Евклида найдите числа х и у, удовлетворяющие уравнению 30х +12y = НОД(30,12). х=1, у=-2, НОД = 6. Где ошибка? |
Криптографические алгоритмы с открытым ключом и их использование
Вопросы практического использования алгоритма RSA
На протяжении многих лет алгоритм RSA активно используется как в виде самостоятельных криптографических продуктов, так и в качестве встроенных средств в популярных приложениях. Открытое шифрование на базе алгоритма RSA применяется в популярном пакете шифрования PGP, операционной системе Windows, различных Интернет-браузерах, банковских компьютерных системах. Кроме того, различные международные стандарты шифрования с открытым ключом и формирования цифровой подписи используют RSA в качестве основного алгоритма.
Для обеспечения высокой надежности шифрования необходимо, чтобы выступающее в качестве модуля число N было очень большим – несколько сотен или тысяч бит. Только в этом случае будет практически невозможно по открытым параметрам определить закрытый ключ. Так, известно, что в конце 1995 года удалось практически реализовать раскрытие шифра RSA для 500-значного модуля. Для этого с помощью сети Интернет было задействовано более тысячи компьютеров.
Сами авторы RSA рекомендовали использовать следующие размеры модуля N: 768 бит - для частных лиц; 1024 бит - для коммерческой информации; 2048 бит - для особо секретной информации. С момента получения их рекомендаций прошло какое-то время, поэтому современные пользователи должны делать поправки в сторону увеличения размера ключей. Однако, чем больше размер ключей, тем медленнее работает система. Поэтому увеличивать размер ключа без необходимости не имеет смысла.
С размером ключей связан и другой аспект реализации RSA - вычислительный. При использовании алгоритма вычисления необходимы как при создании ключей, так и при шифровании/расшифровании, при этом, чем больше размер ключей, тем труднее производить расчеты. Для работы с громадными числами приходится использовать аппарат длинной арифметики. Числа, состоящие из многих сотен бит, не умещаются в регистры большинства микропроцессоров и их приходится обрабатывать по частям. При этом как шифрование, так и расшифрование включают возведение большого целого числа в целую степень по модулю N. При прямых расчетах промежуточные значения были бы невообразимыми. Чтобы упростить процесс вычислений используют специальные алгоритмы для работы с большими числами, основанные на свойствах модульной арифметики, а также оптимизацию при возведении в степень.
Алгоритм RSA реализуется как программным, так и аппаратным путем. Многие мировые фирмы выпускают специализированные микросхемы, производящие шифрование алгоритмом RSA. Программные реализации значительные медленнее, чем аппаратные. К достоинствам программного шифрования RSA относится возможность гибкой настройки параметров, возможность интеграции в различные программные пакеты. В целом, и программная, и аппаратная реализации RSA требуют для выполнения примерно в тысячи раз большего времени по сравнению с симметричными алгоритмами, например ГОСТ 28147-89.
Алгоритм RSA может использоваться для формирования электронной цифровой подписи, а также и для обмена ключами. Возможность применения алгоритма RSA для получения электронной подписи связана с тем, что секретный и открытый ключи в этой системе равноправны. Каждый из ключей, d или e, могут использоваться как для шифрования, так и для расшифрования. Это свойство выполняется не во всех криптосистемах с открытым ключом. Использование алгоритма RSA для формирования ЭЦП рассматривается в "Электронная цифровая подпись" .
Алгоритм Диффи-Хеллмана
Основные сведения
Первая публикация данного алгоритма появилась в 70-х годах ХХ века в статье Диффи и Хеллмана, в которой вводились основные понятия криптографии с открытым ключом. Алгоритм Диффи-Хеллмана не применяется для шифрования сообщений или формирования электронной подписи. Его назначение – в распределении ключей. Он позволяет двум или более пользователям обменяться без посредников ключом, который может быть использован затем для симметричного шифрования. Это была первая криптосистема, которая позволяла защищать информацию без использования секретных ключей, передаваемых по защищенным каналам. Схема открытого распределения ключей, предложенная Диффи и Хеллманом, произвела настоящую революцию в мире шифрования, так как снимала основную проблему классической криптографии – проблему распределения ключей.
Алгоритм основан на трудности вычислений дискретных логарифмов. Попробуем разобраться, что это такое. В этом алгоритме, как и во многих других алгоритмах с открытым ключом, вычисления производятся по модулю некоторого большого простого числа Р. Вначале специальным образом подбирается некоторое натуральное число А, меньшее Р. Если мы хотим зашифровать значение X, то вычисляем
Y = AX mod P.
Причем, имея Х, вычислить Y легко. Обратная задача вычисления X из Y является достаточно сложной. Экспонента X как раз и называется дискретным логарифмом Y. Таким образом, зная о сложности вычисления дискретного логарифма, число Y можно открыто передавать по любому каналу связи, так как при большом модуле P исходное значение Х подобрать будет практически невозможно. На этом математическом факте основан алгоритм Диффи-Хеллмана для формирования ключа.
Формирование общего ключа
Пусть два пользователя, которых условно назовем пользователь 1 и пользователь 2, желают сформировать общий ключ для алгоритма симметричного шифрования. Вначале они должны выбрать большое простое число Р и некоторое специальное число А, 1 < A < P-1, такое, что все числа из интервала [1, 2, ..., Р-1] могут быть представлены как различные степени А mod Р. Эти числа должны быть известны всем абонентам системы и могут выбираться открыто. Это будут так называемые общие параметры.
Затем первый пользователь выбирает число Х1 (X1<P), которое желательно формировать с помощью датчика случайных чисел. Это будет закрытый ключ первого пользователя, и он должен держаться в секрете. На основе закрытого ключа пользователь 1 вычисляет число
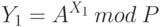
которое он посылает второму абоненту.
Аналогично поступает и второй пользователь, генерируя Х2 и вычисляя
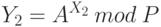
Это значение пользователь 2 отправляет первому пользователю.
После этого у пользователей должна быть информация, указанная в следующей таблице:
Из чисел Y1 и Y2, а также своих закрытых ключей каждый из абонентов может сформировать общий секретный ключ Z для сеанса симметричного шифрования. Вот как это должен сделать первый пользователь:
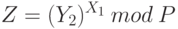
Никто другой кроме пользователя 1 этого сделать не может, так как число Х1 секретно. Второй пользователь может получить то же самое число Z, используя свой закрытый ключ и открытый ключ своего абонента следующим образом:

Если весь протокол формирования общего секретного ключа выполнен верно, значения Z у одного и второго абонента должны получиться одинаковыми. Причем, что самое важное, противник, не зная секретных чисел Х1 и Х2, не сможет вычислить число Z. Не зная Х1 и Х2, злоумышленник может попытаться вычислить Z, используя только передаваемые открыто Р, А, Y1 и Y2. Безопасность формирования общего ключа в алгоритме Диффи-Хеллмана вытекает из того факта, что, хотя относительно легко вычислить экспоненты по модулю простого числа, очень трудно вычислить дискретные логарифмы. Для больших простых чисел размером сотни и тысячи бит задача считается неразрешимой, так как требует колоссальных затрат вычислительных ресурсов.
Пользователи 1 и 2 могут использовать значение Z в качестве секретного ключа для шифрования и расшифрования данных. Таким же образом любая пара абонентов может вычислить секретный ключ, известный только им.
