|
С помощью обобщенного алгоритма Евклида найдите числа х и у, удовлетворяющие уравнению 30х +12y = НОД(30,12). х=1, у=-2, НОД = 6. Где ошибка? |
Поточные шифры и генераторы псевдослучайных чисел. Часть 1
Генератор псевдослучайных чисел на основе алгоритма BBS
Широкое распространение получил алгоритм генерации псевдослучайных чисел, называемый алгоритмом BBS (от фамилий авторов — L. Blum, M. Blum, M. Shub) или генератором с квадратичным остатком. Для целей криптографии этот метод предложен в 1986 году.
Он заключается в следующем. Вначале выбираются два больших простых1 Целое положительное число большее единицы называется простым, если оно не делится ни на какое другое число, кроме самого себя и единицы. Подробнее о простых числах см. в "Основные положения теории чисел, используемые в криптографии с открытым ключом" . числа p и q. Числа p и q должны быть оба сравнимы с 3 по модулю 4, то есть при делении p и q на 4 должен получаться одинаковый остаток 3. Далее вычисляется число M = p* q, называемое целым числом Блюма. Затем выбирается другое случайное целое число х, взаимно простое (то есть не имеющее общих делителей, кроме единицы) с М. Вычисляем х0= х2mod M. х0 называется стартовым числом генератора.
На каждом n-м шаге работы генератора вычисляется хn+1= хn2 mod M. Результатом n-го шага является один (обычно младший) бит числа хn+1. Иногда в качестве результата принимают бит чётности, то есть количество единиц в двоичном представлении элемента. Если количество единиц в записи числа четное – бит четности принимается равным 0, нечетное – бит четности принимается равным 1.
Например, пусть p = 11, q = 19 (убеждаемся, что 11 mod 4 = 3, 19 mod 4 = 3). Тогда M = p* q = 11*19=209. Выберем х, взаимно простое с М: пусть х = 3. Вычислим стартовое число генератора х0:
х0 = х2 mod M = 32 mod 209 = 9 mod 209 = 9.
Вычислим первые десять чисел хi по алгоритму BBS. В качестве случайных бит будем брать младший бит в двоичной записи числа хi:
| х1=92 mod 209= 81 mod 209= 81 | младший бит: | 1 |
| х2=812 mod 209= 6561 mod 209= 82 | младший бит: | 0 |
| х3=822 mod 209= 6724 mod 209= 36 | младший бит: | 0 |
| х4=362 mod 209= 1296 mod 209= 42 | младший бит: | 0 |
| х5=422 mod 209= 1764 mod 209= 92 | младший бит: | 0 |
| х6=922 mod 209= 8464 mod 209= 104 | младший бит: | 0 |
| х7=1042 mod 209= 10816 mod 209= 157 | младший бит: | 1 |
| х8=1572 mod 209= 24649 mod 209= 196 | младший бит: | 0 |
| х9=1962 mod 209= 38416 mod 209= 169 | младший бит: | 1 |
| х10=1692 mod 209= 28561 mod 209= 137 | младший бит: | 1 |
Самым интересным для практических целей свойством этого метода является то, что для получения n-го числа последовательности не нужно вычислять все предыдущие n чисел хi. Оказывается хn можно сразу получить по формуле
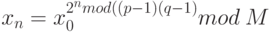
Например, вычислим х10 сразу из х0:
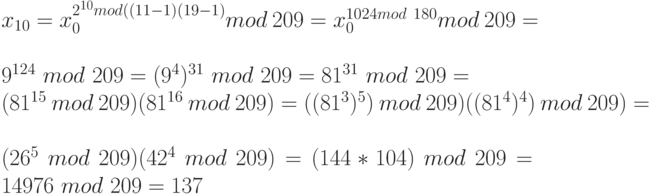
В результате действительно получили такое же значение, как и при последовательном вычислении, – 137. Вычисления кажутся достаточно сложными, однако на самом деле их легко оформить в виде небольшой процедуры или программы и использовать при необходимости.
Возможность "прямого" получения хn позволяет использовать алгоритм BBS при потоковой шифрации, например, для файлов с произвольным доступом или фрагментов файлов с записями базы данных.
Безопасность алгоритма BBS основана на сложности разложения большого числа М на множители. Утверждается, что если М достаточно велико, его можно даже не держать в секрете; до тех пор, пока М не разложено на множители, никто не сможет предсказать выход генератора ПСЧ. Это связано с тем, что задача разложения чисел вида n = pq (р и q — простые числа) на множители является вычислительно очень трудной, если мы знаем только n, а р и q — большие числа, состоящие из нескольких десятков или сотен бит (это так называемая задача факторизации).
Кроме того, можно доказать, что злоумышленник, зная некоторую последовательность, сгенерированную генератором BBS, не сможет определить ни предыдущие до нее биты, ни следующие. Генератор BBS непредсказуем в левом направлении и в правом направлении. Это свойство очень полезно для целей криптографии и оно также связано с особенностями разложения числа М на множители.
Самым существенным недостатком алгоритма является то, что он недостаточно быстр, что не позволяет использовать его во многих областях, например, при вычислениях в реальном времени, а также, к сожалению, и при потоковом шифровании.
Зато этот алгоритм выдает действительно хорошую последовательность псевдослучайных чисел с большим периодом (при соответствующем выборе исходных параметров), что позволяет использовать его для криптографических целей при генерации ключей для шифрования.
Ключевые термины
Stream cipher – поточный шифр.
Алгоритм BBS – один из методов генерации псевдослучайных чисел. Название алгоритма происходит от фамилий авторов - L. Blum, M. Blum, M. Shub. Алгоритм может использоваться в криптографии. Для вычислений очередного числа xn+1 по алгоритму BBS используется формула хn+1= хn2 mod M, где M = pq является произведением двух больших простых p и q.
Генератор псевдослучайных чисел (ГПСЧ) – некоторый алгоритм или устройство, которые создают последовательность битов, внешне похожую на случайную.
Линейный конгруэнтный генератор псевдослучайных чисел – один из простейших ГПСЧ, который для вычисления очередного числа ki использует формулу ki=(a*ki-1+b)mod c, где а, b, с — некоторые константы, a ki-1 — предыдущее псевдослучайное число.
Метод Фибоначчи с запаздываниями – один из методов генерации псевдослучайных чисел. Может использоваться в криптографии.
Поточный шифр – шифр, который выполняет шифрование входного сообщения по одному биту (или байту) за операцию. Поточный алгоритм шифрования устраняет необходимость разбивать сообщение на целое число блоков. Поточные шифры используются для шифрования данных в реальном времени.
Краткие итоги
Поточный шифр – это шифр, который выполняет шифрование входного сообщения по одному биту (или байту) за операцию. Поточный алгоритм шифрования устраняет необходимость разбивать сообщение на целое число блоков. Таким образом, если передается поток символов, каждый символ может шифроваться и передаваться сразу. Поточные шифры используются для шифрования данных в режиме реального времени.
В качестве генераторов ключей в поточных шифрах могут использоваться генераторы псевдослучайных чисел (ГПСЧ). Целью использования ГПСЧ является получение "бесконечного" ключевого слова, располагая относительно малой длиной самого ключа. Для использования в криптографических целях генератор псевдослучайных чисел должен обладать некоторыми свойствами, например, период последовательности, порождаемой генератором, должен быть очень большой.
Простейшими генераторами псевдослучайных чисел являются: линейный конгруэнтный генератор, генератор по методу Фибоначчи с запаздываниями, генератор на основе алгоритма Блюм – Блюма – Шуба (BBS).
Набор для практики
Вопросы для самопроверки
- Чем поточный шифр отличается от блочного?
- Каким образом организуется шифрование потока данных переменной длины?
- Какие числа называют "псевдослучайными"?
- Какими свойствами должен обладать генератор псевдослучайных чисел для использования в криптографических целях?
- Какие генераторы псевдослучайных чисел Вы можете назвать?
- Перечислите основные характеристики, достоинства и недостатки каждого из рассмотренных в данной лекции генераторов псевдослучайных чисел.
Упражнения для самопроверки
- Определите последовательность из первых десяти чисел и период линейного конгруэнтного генератора ПСЧ для различных параметров а, b и c (k0 принять равным 0):
- а =5, b =7 и c = 17;
- а = 6, b =3 и c = 23.
- Вычислите последовательность из десяти чисел, генерируемую методом Фибоначчи с запаздыванием начиная с kа при следующих исходных данных:
- a = 3, b = 1, k0=0.6; k1=0.3; k2=0.5;
- a = 4, b = 2, k0=0.9; k1=0.3; k2=0.5; k3=0.9.
- Значения k0, k1, k2, k3, полученные с помощью линейного конгруэнтного генератора, равны: k0 = 1, k1 = 12, k2 = 3, k3 = 6. Найдите параметры а, b и c генератора ПСЧ.
- Вычислить х11 по методу генерации псевдослучайных чисел BBS, если p = 11, q = 19, х = 3.
