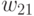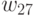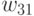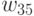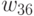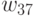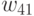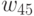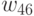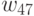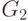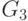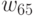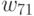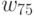Компоновка модулей. Методы разбиения электрических схем на функционально законченные модули
19.5. Итерационные алгоритмы улучшения начального разбиения
Сущность данной группы алгоритмов заключается в выборе некоторого начального "разрезания" исходного графа на куски (вручную или с помощью последовательного метода компоновки) и последующего его улучшения с помощью итерационного парного или группового обмена вершин из различных кусков. При этом для каждой итерации осуществляется перестановка тех вершин, которая обеспечивает максимальное уменьшение числа связей между кусками графа или максимальное улучшение другого выбранного показателя качества с учётом используемых ограничений.
С этой целью в матрице  выделяем по главной диагонали две подматрицы:
выделяем по главной диагонали две подматрицы: 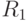 и
и 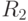 . При этом порядок подматрицы
. При этом порядок подматрицы 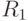 равен числу вершин, которые должны находиться в первом куске, а порядок подматрицы
равен числу вершин, которые должны находиться в первом куске, а порядок подматрицы 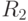 - числу всех оставшихся вершин графа (табл. 19.3).
- числу всех оставшихся вершин графа (табл. 19.3).
После того, как переставим строки и столбцы матрицы  , подматрицу
, подматрицу 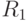 из матрицы
из матрицы  исключаем, вычеркнув из
исключаем, вычеркнув из  строки и столбцы, соответствующие элементам
строки и столбцы, соответствующие элементам 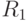 .
.
Далее подматрицу 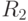 разбиваем снова на две подматрицы
разбиваем снова на две подматрицы 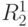 и
и 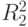 , причем порядок
, причем порядок 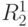 соответствует числу вершин второго выделяемого куска, а порядок
соответствует числу вершин второго выделяемого куска, а порядок 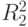 - числу оставшихся вершин графа. Переставляем строки и столбцы
- числу оставшихся вершин графа. Переставляем строки и столбцы 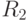 с целью минимизации числа соединительных рёбер. После этого подматрица
с целью минимизации числа соединительных рёбер. После этого подматрица 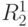 исключается и процесс повторяется до тех пор, пока не будет выполнено разбиение графа
исключается и процесс повторяется до тех пор, пока не будет выполнено разбиение графа  на "
на "  " кусков.
" кусков.
В нашем случае - 3 куска.
Для каждой вершины графа вводится числовая характеристика, использующая локальную степень этой вершины. Эта характеристика должна количественно оценивать связь рассматриваемой вершины с другими вершинами, лежащими внутри данного куска, по отношению к вершинам, находящимся вне куска.
Эта характеристика называется числом связности.
Пусть, 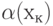 или
или 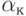 - число связности вершины
- число связности вершины 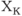 :
:
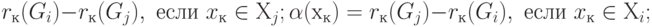 |
( 19.8) |
здесь 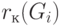 - число рёбер, соединяющих вершину
- число рёбер, соединяющих вершину 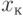 с вершинами куска
с вершинами куска 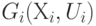 ;
;
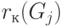 - число рёбер, соединяющих вершину
- число рёбер, соединяющих вершину 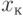 с вершинами куска
с вершинами куска  .
.
 |
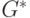 |
||||||||
|---|---|---|---|---|---|---|---|---|---|
 |
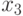 |
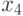 |
 |
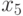 |
 |
 |
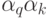 |
||
 |
0 | 1 | 2 | 0 | 0 | 0 | 0 | -3 | |
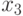 |
1 | 0 | 2 | 0 | 0 | 1 | 1 | -1 | |
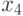 |
2 | 2 | 0 | 1 | 0 | 0 | 0 | -3 | |
| . | |||||||||
 |
0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | |
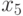 |
0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | |
 |
0 | 0 | 1 | 0 | 1 | 0 | 1 | -1 | |
 |
0 | 0 | 0 | 0 | 0 | 1 | 0 | -1 | |
Физический смысл числа связности следующий.
Значение 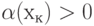 означает, что при переносе вершины
означает, что при переносе вершины  ,
лежащей в куске
,
лежащей в куске 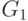 , в кусок
, в кусок 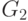 число соединительных рёбер между этими кусками уменьшится на 1.
число соединительных рёбер между этими кусками уменьшится на 1.
Равенство 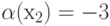 говорит о том, что
говорит о том, что  что при перестановке вершины
что при перестановке вершины 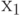 , лежащей в куске
, лежащей в куске 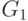 , в кусок
, в кусок 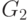 число рёбер в сечении увеличивается на соответствующее количество единиц.
число рёбер в сечении увеличивается на соответствующее количество единиц.
Равенство 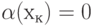 означает, что при перестановке вершины
означает, что при перестановке вершины  из куска
из куска 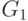 в кусок
в кусок 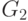 число соединительных рёбер останется без изменения.
число соединительных рёбер останется без изменения.
Задача разбиения заданного графа  с помощью итерационного алгоритма,
заключается в том, чтобы переставить строки и столбцы таким образом, чтобы число ребер,
соединяющих куски графа, было минимальным.
с помощью итерационного алгоритма,
заключается в том, чтобы переставить строки и столбцы таким образом, чтобы число ребер,
соединяющих куски графа, было минимальным.
Построим дополнительную матрицу 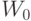 , элементы которой определяются по формуле:
, элементы которой определяются по формуле:

Отсюда для элементов 1-й строки матрицы:
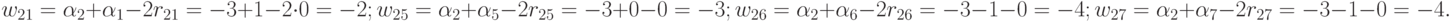
для элементов 2-й строки матрицы:
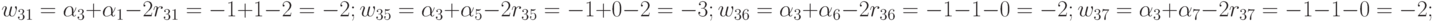
для элементов 3-й строки матрицы:
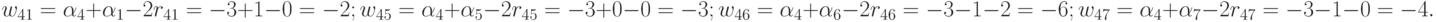
Построим дополнительную матрицу  (табл. 19.4,табл. 19.5)
(табл. 19.4,табл. 19.5)
Для оставшихся частей графа матрицы смежности будут иметь вид (табл. 19. 6):
где
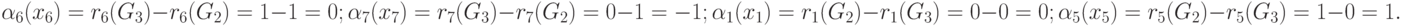
Построим дополнительную матрицу 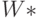 , элементы которой оределяются по формуле:
, элементы которой оределяются по формуле:
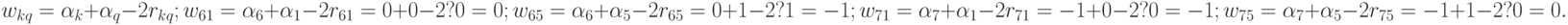
Видим, что в матрице 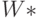 нет положительных элементов, следовательно, перестановка строк и столбцов не приведёт к изменению первоначального разбиения графа, и куски останутся прежними.
нет положительных элементов, следовательно, перестановка строк и столбцов не приведёт к изменению первоначального разбиения графа, и куски останутся прежними.
Контрольные вопросы
- Покажите иерархию конструктивных частей РЭС.
- Поясните понятия компоновки "снизу вверх" и "сверху вниз".
- Какие характерные классы выделяют среди задач компоновки?
- Что является целью разбиения схемы на функционально законченные части?
- Каковы основные критерии задач компоновки/размещения?
- Что принимают в качестве ограничений в задачах компоновки/ разбиения?
- Дайте математическую формулировку задачи разбиения.
- Что называется разбиением графа?
- Что называется коэффициентом разбиения графа?
- Дайте общую характеристику алгоритмов компоновки.
- Как осуществляется работа последовательного алгоритма разбиения?
- Что называют числами связности?
- Как строится дополнительная матрица W?
- Как осуществляется работа итерационного алгоритма с использованием чисел связности?

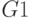 :
:
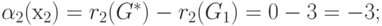
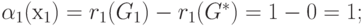
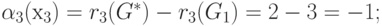
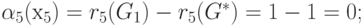
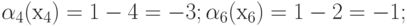
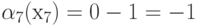 .
.