Моделирование и оптимизация в проектировании технологии
Показать роль математических моделей в управлении качеством наукоемкой промышленной продукции.
5.1. Модели в системном анализе
Принципиальная особенность системного анализа - широкое использование на всех языках методологии моделей систем. Модель является основным рабочим инструментом системного анализа. Модель - это, прежде всего, средство отображения реальной системы, а построение модели - это процесс уяснения общих свойств системы и закономерностей ее функционирования и развития, т. е. овладения систематическими методами построения моделей систем - необходимое условие овладения методологией системного анализа.
В общем случае системы делят на реальные и абстрактные. Абстрактные системы представляют собой математические модели реальных систем, отражающие их основные свойства. В зависимости от выбора различных существенных черт системы (элементов и связей между ними) можно получить различные модели, описывающие с различных точек зрения реальную систему.
С введением понятия математической модели претерпело изменение и понятие "технологический процесс", используемое в научно-технической литературе.
Раньше технологический процесс рассматривался как часть производственного процесса, состоящего из совокупности технологических операций, выполнение которых приводило к получению готового продукта или полуфабриката. При этом сложный многомерный процесс расчленялся на ряд подпроцессов, характеризующихся малым количеством параметров и однотипной физической, химической, электрической природой. Такие мелкие подпроцессы удобнее было описывать с помощью математических моделей, анализировать их поведение и связи.
Однако внедрение систем автоматизации во все сферы проектирования и управления технологическими процессами привело к более широкому его понятию. Этому изменению в значительной степени способствовало создание и использование ранее известных многочисленных математических методов и способов, создание алгоритмов для работы с многомерными, сложными объектами, процессы в которых подвергаются воздействию различных случайных факторов.
Понятие технологического процесса приблизилось в настоящее время к понятию процесса, определенного Норбертом Винером при создании им основных принципов кибернетики как процесс "передачи, хранения и переработки информации".
Технологические процессы сейчас рассматриваются как совокупность действий людей, математических и технических средств, включающую на определенных этапах процессы экономические и социально-политические.
Такое изменение понятия технологического процесса привело к изменению понятия его идентификации, т. е. определение его структуры, параметров, свойств и т. д. Если раньше идентификация процесса в смысле построения его модели означала, прежде всего, выявление физических свойств в виде описания электрических, физических, тепловых и др. процессов, то сейчас понятие идентификации значительно расширилось и формализовалось.
Задача идентификации является в настоящее время составной частью задач автоматизации проектирования и управления технологическим процессом.
Выделение идентификации в самостоятельную задачу делается обычно из чисто методологических соображений, т.к. методы синтеза модели существенно отличаются от методов синтеза управления.
Под идентификацией понимается определение характеристик "вход-выход" объекта путем активного или пассивного эксперимента, причем структура связей входных и выходных переменных считается известной. По мере развития системы идентификация предусматривает непрерывно уточняющуюся модель объекта. Это адаптивные, самонастраивающиеся и т. п. системы. Для сложных многомерных, многосвязных объектов при наличии наблюдаемых (неуправляемых) входных переменных определение характеристик возможно только в условиях нормальной эксплуатации объекта.
При решении практических задач, в том числе при идентификации технологического процесса, не представляется возможным учесть в модели все переменные и все внутренние связи между многочисленными переменными. Поэтому построение модели осуществляется по относительно небольшому количеству переменных. Выбор этих переменных определяется целью построения модели, наличием технических средств передачи и обработки необходимой информации, уровнем теории, имеющимися алгоритмами и математическим обеспечением.
Четко сформулированные цели и требования к системе управления технологическим процессом являются той основой, которая должна быть обеспечена строящейся моделью.
Для того чтобы можно было судить о том, какая построена модель, удовлетворяет ли она предъявляемым к ней требованиям, необходимо уметь количественно оценить уровень наших знаний о технологическом процессе, степень соответствия модели реальному процессу. С этой целью вводится количественная мера степени идентичности ( адекватности, изоморфности) модели реальному процессу, объекту. При построении такой меры, естественно, стремятся к тому, чтобы она базировалась на тех характеристиках, которые используются при идентификации объекта, и могла быть определена по этим характеристикам или непосредственно по данным "вход-выход".
Особенностью технологического процесса, как уже отмечалось, является вероятностный характер. Все измеряемые входные переменные не определяют однозначно выхода объекта. Степень идентичности модели для разных объектов различна, но никогда не достигает единицы. Это является следствием многих причин: недостаточной изученности процесса, отсутствия точного математического описания, отсутствия необходимых датчиков для измерения технологических параметров. Степень связи, т.е. отношение условной дисперсии выхода относительно всех входных переменных к дисперсии выходной величины колеблется от 0, 3 до 0, 95 и редко бывает больше. Таким образом, остаточная дисперсия, т.е. дисперсия выхода, при применении идеальной системы управления не равна нулю. Остаточная дисперсия для физических моделей значительно больше, чем для моделей, полученных с помощью методов идентификации.
Математическое моделирование обязательно включает три взаимосвязанные стадии:
- формализацию изучаемого процесса - построение математической модели (математического описания);
- программирование решения задачи (алгоритмизацию) для нахождения численных значений определяемых параметров;
- установление соответствия ( адекватности ) модели изучаемому процессу.
Построение модели - самая тонкая и ответственная часть математического моделирования. При этом требуется не только и не столько знание математики, сколько глубокое понимание сущности описываемых явлений.
Существует много способов определения модели технологических процессов. Каждый способ дает возможность построить модель, адекватную процессу в том или ином смысле, что зависит от выбранного критерия. Таким образом, применяя множество способов, можно получить множество моделей, изоморфных физическому объекту.
Поэтому при выборе структуры модели и критерия адекватности модели процессу необходимо исходить из цели моделирования процесса, из той задачи, которая стоит перед исследователем при разработке модели.
В общем виде математической моделью (математическим описанием) называют совокупность математических уравнений, которые отражают зависимость выходных величин от входных, дополненную ограничениями, накладываемыми на эти величины условиями физической осуществимости, требованиями безопасности функционирования, уравнениями связи с другими объектами.
Математическое описание, составляющее структуру модели, может быть представлено в виде системы алгебраических и дифференциальных уравнений, отражающих взаимное влияние различных параметров, причем присутствие в математическом описании уравнений одного вида (например, алгебраических) не исключает возможности наличия уравнений и другого вида (дифференциальных).
Необходимо, чтобы модель достаточно верно описывала качественно и количественно свойства моделируемого процесса, т. е. она должна быть адекватна моделируемому процессу. Для проверки адекватности математической модели реальному процессу нужно сравнить результаты измерений в ходе процесса с результатами предсказания модели в идентичных условиях (при определенных значениях параметров).
Конечной целью разработки математических моделей является предсказание ( прогнозирование ) результатов проведения технологического процесса и выработка рекомендаций (или управляющих воздействий) по возможным воздействиям на его ход.
Математические описания объектов проектирования усложняются и видоизменяются от одного этапа проектирования к другому. Более того, даже на одном этапе может быть использовано несколько разных математических описаний ( моделей ). Множество математических моделей, применяемых за время всего процесса проектирования, включает модели различных типов и по форме, и по содержанию.
Наиболее простыми математическими моделями объекта проектирования или управления (прибора, агрегата, цеха т. д.) являются его детерминированные (точно определенные), статистические и стационарные модели. Детерминированные модели не учитывают случайные изменения параметров, статистические - игнорируют переходные процессы (например, вследствие их быстрого протекания), стационарные пренебрегают медленными изменениями характеристик объекта во времени.
Более сложными являются детерминированные динамические модели объектов управления, отражающие влияние на объект значений входных воздействий не только в данный момент, но и в прошлые моменты времени.
Еще более сложны статистические и динамические стохастические модели, когда все процессы в объекте или их часть описываются случайными функциями времени, и для решения задач управления приходится использовать гораздо более сложный математический аппарат теории вероятностей и математической статистики.
5.2. ММ технологического процесса
Эти модели связывают все измеряемые показатели качества выпускаемого изделия (т. е. как количественные, так и качественные его характеристики) с параметрами технологического процесса.
Как уже указывалось выше, особенностью большинства технологических процессов является их стохастический характер, что определяет выбор вида их математической модели. Наиболее эффективными для решения задач идентификации и управления качеством продукции как результата технологического процесса признаны статистические методы.
Статистические методы дают возможность не только описать технологические процессы в виде математических формул, которые отражают закономерности, происходящие в каждом из процессов, и взаимосвязи между ними. Эти методы позволяют получать такие важные практические показатели, как точность результатов каждого из процессов и работы в целом, произвести оценку качества выпускаемой продукции на каждой стадии обработки, определить уровень наладки, разработать методы контроля и многие другие.
Анализ статистических формул дает возможность установить наиболее рациональные пути ведения процесса производства, разработать требования (технические условия) на поставляемое сырье и заготовки, правильно выбрать режимы. Математический анализ закономерностей процессов дает возможность значительно сократить затраты времени и средств на проведение экспериментальных работ, т. к. основные выводы в результате теоретического анализа позволяют установить главные характеристики технологической линии при изменении отдельных показателей каждого из процессов. Таким образом, анализ технологического процесса заключается в том, чтобы установить такие характеристики каждой из операций процесса в целом, чтобы с наименьшими затратами и наибольшей производительностью обеспечить выпуск продукции высокого качества. Для решения этих вопросов широко применяются статистические методы.
увеличить изображение
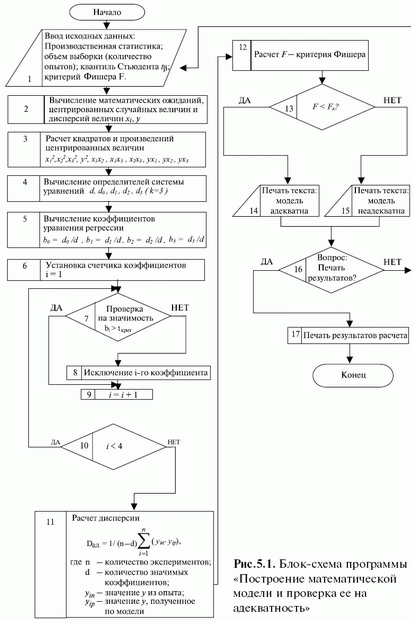
Рис. 5.1. Блок-схема программы "Построение математической модели и проверка ее на адекватность"
На рис. 5.1 приведена блок-схема алгоритма построения математических моделей. Структура уравнения регрессии задается априори, например, для простого случая:
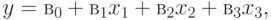
где  - выходная величина (показатель качества );
- выходная величина (показатель качества );
 ,
,  ,
, 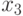 - входные величины (измеряемые параметры процесса);
- входные величины (измеряемые параметры процесса);
 ,
,  ,
,  ,
, 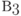 - коэффициенты уравнений регрессии,
определяемые из
- коэффициенты уравнений регрессии,
определяемые из
экспериментов
Количество слагаемых зависит от числа входных параметров, количество уравнений - от числа выходных показателей качества.
Рассмотрим блок-схему алгоритма.
Блок 1. Ввод исходных данных - параметров технологического процесса 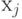 ,
признаков качества готовой продукции
,
признаков качества готовой продукции  ,
объем выборки,
критерий Стьюдента - для определении значимости коэффициентов регрессии,
и критерий Фишера - для оценки адекватности построенной математической модели. Критерии определяются по соответствующим таблицам,
в зависимости от доверительной вероятности и объема выборки. Осуществляется проверка данных и,
при необходимости,
корректировка.
,
объем выборки,
критерий Стьюдента - для определении значимости коэффициентов регрессии,
и критерий Фишера - для оценки адекватности построенной математической модели. Критерии определяются по соответствующим таблицам,
в зависимости от доверительной вероятности и объема выборки. Осуществляется проверка данных и,
при необходимости,
корректировка.
Блок 2. Вычисление оценок статистических характеристик: математического ожидания, дисперсии, среднеквадратического отклонения, центрированных случайных величин. Речь идет об оценках потому, что они рассчитываются для ограниченной выборки, взятой из всей генеральной совокупности, а результаты распространяются на всю генеральную совокупность.
Блок 3. Промежуточные расчеты.
Блок 4. Для определения коэффициентов уравнения (уравнений) регрессии рассчитываются определители системы.
Блок 5. Вычисление коэффициентов уравнения (уравнений) регрессии.
Блок 6. Установление счетчика коэффициентов.
Блок 7. В цикле осуществляется проверка коэффициентов на значимость по критерию Стьюдента: если соответствующий коэффициент больше критерия Стьюдента, то он признается значимым и оставляется в уравнении.
Блок 8. В случае если коэффициент меньше критерия Стьюдента, то он исключается из уравнения, производится переход на блок 4, в котором происходит перерасчет определителей, уже без исключенного коэффициента.
Блоки 9-10 обеспечивают рассмотрение в цикле всех коэффициентов. После их рассмотрения получаем окончательное уравнение регрессии, которое необходимо далее проверить на адекватность. Для этого служит блок 11.
Блок 11. Расчет дисперсии адекватности для расчета критерия Фишера.
Блок 12. Расчет критерия Фишера для полученной модели ( моделей ).
Блок 13. Осуществляется сравнение рассчитанного значения критерия Фишера с табличным его значением. Если расчетное значение меньше табличного, то модель признается адекватной, и ее можно использовать для прогнозирования качества производимой продукции.
В случае получения неадекватной математической модели следует переходить к нелинейной модели, т. е. вводить квадратичные члены и эффекты взаимодействия, например, для приведенного выше простого уравнения добавятся такие члены: