Разработка "сквозных" математических моделей технологического процесса как основа АСНИ
Показать необходимость и сущность предварительной обработки производственной информации для корректного перехода к построению математических (технологических) моделей.
4.1. Исходные данные для построения математических моделей
Для выполнения проектов систем автоматизированных технологических комплексов, как уже было сказано, необходимо построение математических моделей (ММ). Для этого должны быть представлены такие исходные данные и материалы:
- уточненные технологические схемы с характеристиками оборудования;
- перечни контролируемых и регулируемых параметров с необходимыми требованиями (например, нормами, контрольными границами регулирования);
- чертежи производственных помещений с расположением технологического оборудования;
- чертежи технологического оборудования, на котором предусматривается установка приборов и средств автоматизации;
- требования к надежности систем автоматизации;
- техническая документация по типовым и проектным решениям;
- другие.
Для выполнения перечисленных пунктов необходимо, в первую очередь, разработать структурную схему проектируемого или исследуемого технологического процесса с указанием контрольных точек и контролируемых параметров. Значения этих параметров на всех контрольных точках и будут представлять исходные данные для построения математических моделей.
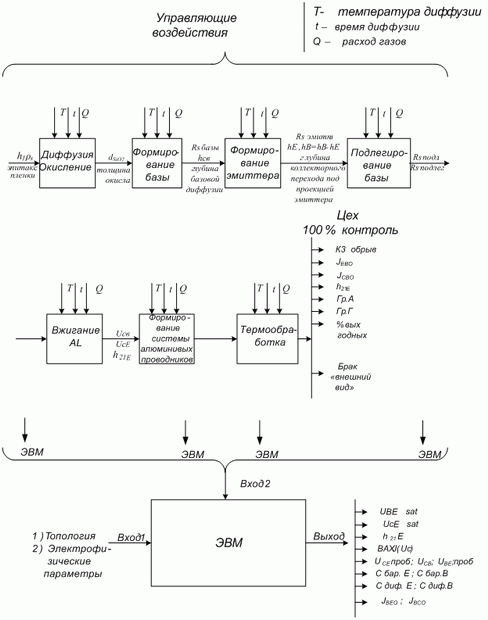
На рис. 4.1 и 4.2 представлены такие схемы для технологических процессов изготовления видеоконтрольного устройства и транзисторов.
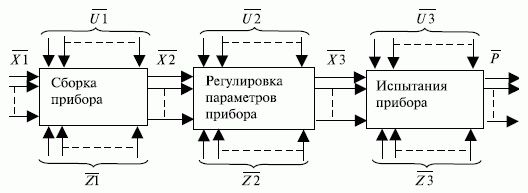
Рис. 4.1. Структурная схема технологического процесса изготовления видеоконтрольного устройства (ВКУ)
Здесь: 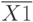 - совокупность параметров комплектующих элементов;
- совокупность параметров комплектующих элементов;
 - совокупность контролируемых параметров модулей ВКУ и показателей надежности собранного прибора до регулировки;
- совокупность контролируемых параметров модулей ВКУ и показателей надежности собранного прибора до регулировки;
 - совокупность показателей надежности готового ВКУ после регулировки;
- совокупность показателей надежности готового ВКУ после регулировки;
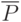 - вектор выходных показателей надежности после испытаний;
- вектор выходных показателей надежности после испытаний;
 ,
,  ,
,  - векторы неконтролируемых возмущений, воздействующих на технологические операции, соответственно, сборки, регулировки и испытаний, например, неконтролируемые параметры технологического оборудования, внешней среды;
- векторы неконтролируемых возмущений, воздействующих на технологические операции, соответственно, сборки, регулировки и испытаний, например, неконтролируемые параметры технологического оборудования, внешней среды;
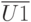 ,
, 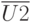 ,
, 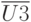 - векторы контролируемых воздействий на технологические операции сборки, регулировки испытаний, например, подаваемые напряжения, токи.
- векторы контролируемых воздействий на технологические операции сборки, регулировки испытаний, например, подаваемые напряжения, токи.
На этих рисунках показан пример определения контрольных точек и контролируемых параметров по ходу ведения технологического процесса. Информация, собранная в течение заданного времени, используется для построения математических моделей в виде уравнений регрессии.
Для управления сложным технологическим процессом требуются описание, учет, измерение и регистрация максимального количества параметров на каждой операции. Однако проведение полного перечня замеров по всему процессу в условиях производства затруднено и не всегда экономически оправдано. Поэтому уже на первых стадиях проектирования технологического процесса очень важно решение такой задачи: найти минимальное количество параметров, несущих максимальное количество информации.
Существуют различные методы, например, методы факторного анализа, для поиска обобщенных факторов и закономерностей при минимальном количестве параметров, несущих достаточную информацию о протекании процесса, закладываемых далее в математические модели в качестве исходных данных.
Основными рекомендациями, выдаваемыми в результате проведения НИР и ОКР, должны быть перечень наиболее информативных ( контролируемых и регулируемых ) параметров, математические модели и алгоритмы управления, эскиз проектируемой системы.
Полученные обобщенные факторы или отдельные параметры, которые вносят наибольший вклад, принимаются за информативные. Они и являются исходными данными при разработке математических моделей технологического процесса, объекта или отдельных технологических операций, т. е. при разработке математической модели системы.
Использование обобщенных факторов в качестве переменных в регрессионном анализе позволяет сократить число переменных, устранить коррелированность переменных, уменьшить влияние ошибок и в случае ортогональности выделенных факторов значительно упростить оценку значимости переменных.
Такой анализ исходной информации целесообразно проводить на самом первом этапе проектирования - формировании технического задания.
Итак, первый этап проектирования системы - внешнее проектирование - содержит в себе синтез, анализ, оптимизацию. Из ряда элементных баз выбирается та, которая бы удовлетворяла поставленным требованиям; к началу проектирования выбирается или синтезируется решение, отвечающее поставленным целям.
Так как цель проектирования - разработка не только допустимого варианта проекта, но и наиболее выгодного в техническом и экономическом отношении, то далее решается задача оптимизации проекта.
4.2. Предварительная обработка исходной информации: сущность и необходимость
Предварительная обработка результатов измерений или наблюдений необходима для того, чтобы в дальнейшем с наибольшей эффективностью, а главное - корректно, использовать для построения эмпирических зависимостей статистические методы.
Содержание предварительной обработки в основном состоит в отсеивании грубых погрешностей измерения или погрешностей, неизбежно возникающих при переписывании цифрового материала или при вводе информации в считывающее устройство ЭВМ.
Рассмотрим возможность использования различных математических методов для отбрасывания грубых погрешностей и проверки гипотезы о нормальном распределении исходных данных.
Грубые погрешности измерения (аномальные, или сильно выделяющиеся, значения) очень плохо поддаются определению, хотя интуитивно каждому экспериментатору ясно, что это такое.
Можно встретить указание, что аномальные значения измеряемой величины получаются в результате изменения условий эксперимента, однако это определение неполное.
Другим важным моментом предварительной обработки данных является проверка соответствия распределения результатов измерения закону нормального распределения. Если эта гипотеза неприемлема, то следует определить, какому закону распределения подчиняются опытные данные, и, если это возможно, преобразовать данное распределение к нормальному. Только после выполнения перечисленных выше операций можно перейти к построению эмпирических формул, применяя, например, метод наименьших квадратов.
Используя введенные обозначения (рис. 3.2), статистические данные о технологическом процессе и качестве продукции можно сгруппировать в виде двух матриц наблюдений  и
и 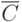 :
:
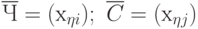 |
( 4.1) |
где
-
 - значение
- значение  -го параметра в
-го параметра в  - цикле;
- цикле; -
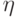 - номер цикла;
- номер цикла; -
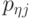 - значение
- значение  -го признака качества в
-го признака качества в  - цикле;
- цикле; -
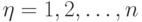 ,
,  - число наблюдений технологических циклов;
- число наблюдений технологических циклов; -
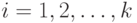 ,
,  - количество параметров процесса;
- количество параметров процесса; -
 ,
,  - количество признаков готового прибора.
- количество признаков готового прибора.
Первый этап математического описания - статистические оценки характеристик генеральной совокупности (всех технологических циклов) по выборке.
Оценка математического ожидания - выборочное среднее арифметическое
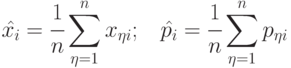 |
( 4.2) |
Оценка дисперсии - выборочная дисперсия
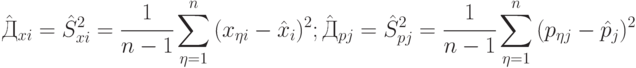 |
( 4.3) |
Оценка стандартного отклонения - выборочное среднеквадратиче-ское отклонение
 |
( 4.4) |
Оценка коэффициента вариации - выборочный коэффициент вариации
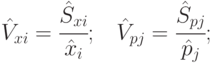 |
( 4.5) |
Оценка коэффициентов парной корреляции - выборочный коэффициент парной корреляции
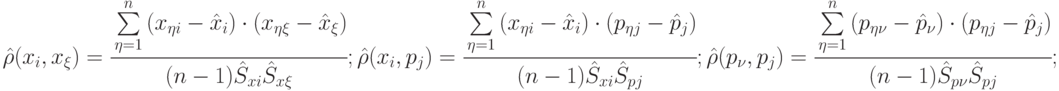 |
( 4.5) |
где 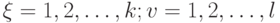 .
.
Отсев грубых погрешностей
Можно встретить большое количество различных рекомендаций для проведения отсева грубых погрешностей наблюдения (аномальных значений). Рассмотрим наиболее простые методы отсева грубых погрешностей. Если в распоряжении экспериментатора имеется выборка небольшого объема  , то можно воспользоваться методом вычисления максимального относительного отклонения:
, то можно воспользоваться методом вычисления максимального относительного отклонения:
 |
( 4.7) |
где 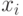 - крайний (наибольший или наименьший) элемент выборки, по которой подсчитывались
- крайний (наибольший или наименьший) элемент выборки, по которой подсчитывались  и
и 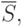
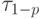 - табличное значение статистики
- табличное значение статистики  , вычисленной при доверительной вероятности
, вычисленной при доверительной вероятности 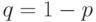 .
.
Таким образом, для выделения аномального значения вычисляют
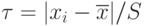 |
( 4.8) |
которое затем сравнивают с табличным значением 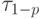 .
.
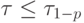 |
( 4.9) |
Если это неравенство соблюдается, то наблюдение не отсеивают; если не соблюдается, то наблюдение исключают. После исключения того или иного наблюдения или нескольких наблюдений характеристики эмпирического распределения должны быть перечитаны по данным сокращенной выборки.
Квантили распределения статистики 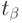 берут при уровнях значимости
берут при уровнях значимости 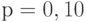 ,
, 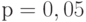 ,
,  ,
, 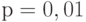 или доверительной вероятности
или доверительной вероятности 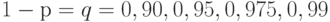 . На практике обычно используют уровень значимости
. На практике обычно используют уровень значимости 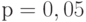 (результат получается с доверительной вероятностью 95%).
(результат получается с доверительной вероятностью 95%).
Процедуру отсева можно повторить и для следующего по абсолютной величине максимального относительного отклонения, но предварительно необходимо пересчитать  и
и  для выборки нового объема
для выборки нового объема 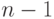 .
.
Рассмотрим другой метод отсева грубых погрешностей для малой выборки. В этом случае вычисляют
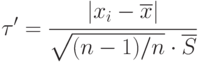 |
( 4.10) |
и полученный результат сравнивают с критическим значением, взятым из таблицы при соответствующих  и
и 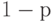 .
.
Отсев грубых погрешностей можно провести и для больших выборок. Для практических целей лучше всего использовать таблицы распределения Стьюдента. Этот метод исключения аномальных значений для выборок большого объема отличается простотой, а таблицы распределения Стьюдента имеются практически в любой книге по математической статистике. Распределение Стьюдента относится к категории распределений, связанных с нормальным распределением. Подробно эти распределения рассмотрены в учебниках по математической статистике.
Известно, что критическое значение  (
( 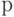 - процентная точка нормированного выборочного отклонения) выражается через критическое значение распределения Стьюдента
- процентная точка нормированного выборочного отклонения) выражается через критическое значение распределения Стьюдента 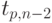
![\tau_(p,n) = \cfrac{ t_{(p,n-2)}\sqrt{n-1}}{\sqrt{n-2+[ t_{(p,n-2)}]^2}}](/sites/default/files/tex_cache/230c0d3616b60032db3ec7bc3dbcacaf.png) |
( 4.11) |
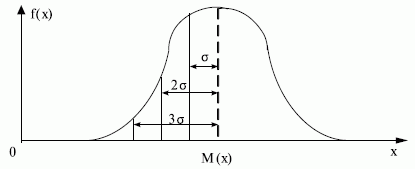
На практике пользуются достаточно удобным методом отсева грубых погрешностей. Если рассматривать кривую нормального распределения (рис. 4.3), то это те значения, которые выходят за пределы  ,
, 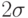 ,
, 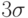 в зависимости от объема выборки и доверительной вероятности. Они просто отбрасываются по "правилу 6 сигма" (на рисунке представлена половина графика).
в зависимости от объема выборки и доверительной вероятности. Они просто отбрасываются по "правилу 6 сигма" (на рисунке представлена половина графика).
Например, для объема выборки  измерений их отсев будет осуществляться при выходе за пределы:
измерений их отсев будет осуществляться при выходе за пределы: