Математические методы описания моделей конструкций РЭС. Некоторые понятия теории множеств
Изложить основные понятия теории множеств, знание которых является обязательным при современном конструкторском проектировании РЭС.
16.1. Определения
Математические методы, положенные в основу алгоритмических процессов конструирования РЭС, а также процессы организации входной и выходной информации о проектируемом объекте широко используют понятия и символы теории множеств.
Под множеством понимают совокупность объектов любой природы, называемых элементами данного множества, обладающих каким-либо общим для множества свойством.
В множестве, по определению, все элементы различны, а порядок перечисления элементов множества произвольный. Следовательно, совокупность элементов 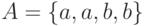 не является множеством.
не является множеством.
Существует два основных способа задания множеств: перечисление и описание.
Первый способ состоит в том, что задаётся и перечисляется полный список элементов, входящих в множество. Например, множество элементов схемы РЭС определяется их списком. Данный способ удобно применять только к ограниченному числу конечных множеств.
Второй способ применяется, когда множество нельзя или затруднительно задать с помощью списка (это может относиться к конечным и бесконечным множествам). В таком случае множества определяются свойствами их элементов.
Множество  считается заданным, если указано свойство
считается заданным, если указано свойство 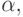 которым обладают все элементы, принадлежащие множеству А, и которым элементы, не принадлежащие множеству
которым обладают все элементы, принадлежащие множеству А, и которым элементы, не принадлежащие множеству  , не обладают.
, не обладают.
Если  - произвольное множество, а
- произвольное множество, а  - некоторое свойство, то запись
- некоторое свойство, то запись

означает множество тех и только тех элементов 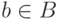 , которые обладают свойством
, которые обладают свойством 
При задании множеств вторым способом необходимо так задавать свойство, характеризующее элементы множества, чтобы оно было общим непротиворечивым для всех его элементов.
Как основное понятие теории, понятие множества не подлежит логическому определению.
Элементы множества могут иметь различную природу. Например, можно говорить о множестве микросхем, входящих в определённую конструкцию РЭС, или о множестве чертежей, входящих в полный комплект конструкторской документации для производства какого-либо изделия.
Множества обозначают заглавными буквами латинского алфавита: 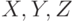 и т.д., а элементы множества - соответствующими строчными буквами того же алфавита:
и т.д., а элементы множества - соответствующими строчными буквами того же алфавита: 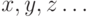 или строчными буквами с индексами:
или строчными буквами с индексами: 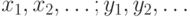 и т.д.
и т.д.
Равенство  свидетельствует о том, что элементы
свидетельствует о том, что элементы  являются элементами множества
являются элементами множества  .
.
Множество можно задавать не только перечислением его элементов, но и с помощью описательного способа, указывающего характерное свойство, которым обладают все элементы этого множества.
Например, если во всём множестве  микросхем электронного блока сложной радиоаппаратуры есть некоторое множество
микросхем электронного блока сложной радиоаппаратуры есть некоторое множество  гибридных интегральных схем, то это можно записать так:
гибридных интегральных схем, то это можно записать так:

Это читается так: множество  состоит из элементов
состоит из элементов  множества
множества  , обладающих тем свойством, что
, обладающих тем свойством, что  является гибридной интегральной схемой.
является гибридной интегральной схемой.
Здесь введено новое обозначение 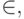 означающее, что объект
означающее, что объект  является элементом множества
является элементом множества  . Если же некоторый объект
. Если же некоторый объект  не принадлежит множеству
не принадлежит множеству  , то это условие записывают в виде
, то это условие записывают в виде  .
.
В том случае, когда не вызывает сомнения, из какого множества берутся элементы  , принадлежность их к множеству
, принадлежность их к множеству  можно не указывать.
можно не указывать.
Например, известно, что множество гибридных интегральных схем входит во множество микросхем того же самого электронного блока, тогда запись будет иметь вид

Число элементов множества 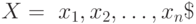 называют мощностью этого множества и обозначают прямыми скобками, например,
называют мощностью этого множества и обозначают прямыми скобками, например,  .
.
Если число элементов множества  конечно, то такое множество называют конечным.В противном случае множество будет бесконечным.
конечно, то такое множество называют конечным.В противном случае множество будет бесконечным.
В теории множеств вводится понятие пустого множества, в котором не содержится ни одного элемента.
Пустое множество обозначают специальным символом 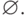 Например, если множество
Например, если множество  пусто, то пишут
пусто, то пишут 
Последовательность из  элементов множества называют n - строкой. В отличие от обычного множества, где порядок элементов безразличен, в
элементов множества называют n - строкой. В отличие от обычного множества, где порядок элементов безразличен, в  - строке обязательно задаётся их определённая последовательность.
- строке обязательно задаётся их определённая последовательность.
Множество  равно множеству
равно множеству  , если оба эти множества состоят из одних и тех же элементов.
, если оба эти множества состоят из одних и тех же элементов.
Если множество  полностью содержится во множестве
полностью содержится во множестве 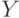 и при этом
и при этом  то говорят, что множество
то говорят, что множество  является подмножеством множества Y:
является подмножеством множества Y:
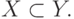
Следовательно, мы рассмотрели два соотношения:
- принадлежность 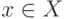 ;
;
- включение  .
.
Первое определяет связь между множеством и его элементами, а второе - между двумя множествами.
В случае, когда  и, одновременно,
и, одновременно, 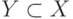 , имеет место равенство
, имеет место равенство 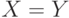 , т.е. множества
, т.е. множества  и
и 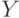 совпадают.
совпадают.
Символическая запись 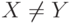 означает, что множество
означает, что множество  не совпадает с множеством
не совпадает с множеством  .
.
