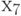Компоновка модулей. Методы разбиения электрических схем на функционально законченные модули
19.3. Алгоритмы разбиения
Известные алгоритмы компоновки можно условно разбить на 5 групп:
- алгоритмы, использующие методы целочисленного программирования;
- последовательные алгоритмы ;
- итерационные алгоритмы ;
- смешанные алгоритмы;
- алгоритмы, основанные на методе ветвей и границ.
Алгоритмы первой группы, хотя и позволяют получить точное решение задачи, однако для устройства реальной сложности фактически не реализуемы на ЭВМ.
Наибольшее распространение получили приближённые алгоритмы компоновки (последовательные, итерационные, смежные).
Суть последовательных алгоритмов разбиения графа заключается в выборе по определённому правилу вершины или группы вершин, к которым присоединяются затем другие вершины графа с целью образования первой части. Далее процесс повторяется для второй части и т.д. до получения желаемого разрезания графа.
При использовании итерационных алгоритмов сначала граф разбивается на определённое число частей произвольным образом либо с помощью последовательного алгоритма. Затем по определённым правилам производится перестановка вершин из одной части в другую с целью минимизации числа внешних рёбер.
Оптимизация компоновки достигается парными или групповыми перестановками вершин графа из различных кусков.
Процесс перераспределения вершин заканчивают при получении локального экстремума целевой функции, удовлетворяющего требованиям разработчика.
В смешанных алгоритмах компоновки для получения начального варианта "разрезания" используется алгоритм последовательного формирования кусков; дальнейшая оптимизация решения осуществляется перераспределением вершин между отдельными кусками графа.
В алгоритмах разбиения, опирающихся на идеи математического программирования, в основном используются методы ветвей и границ и решение задачи о назначении.
Алгоритмы разбиения, использующие методы ветвей и границ, состоят из следующих этапов.
Сначала определяется нижняя оценка разбиения графа на заданное число частей. Затем производится построение дерева решений и осуществляется поиск оптимального результата.
Задачу разбиения графа схемы на части можно свести к задаче о назначении следующим образом.
Сначала отыскивают назначение кандидатов (вершин графа) на все части, дающие минимальные суммарные затраты, причём, каждая вершина графа может быть назначена только в одну часть и в каждой части должны содержаться различные вершины графа.
Важной задачей в общей проблеме конструирования является покрытие, т.е. преобразование функциональных схем в принципиальные.
Под покрытием схемы понимается представление функциональной схемы конструктивными элементами, на которых она будет реализована, и связями между ними.
Конечной целью покрытия является выбор оптимальной элементно-технической базы проектируемого устройства.
19.4. Последовательные алгоритмы разбиения электрической схемы
В последовательных алгоритмах "разрезание" исходного графа 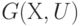 на " l " частей
на " l " частей  c числом вершин в каждой, соответственно,
c числом вершин в каждой, соответственно,  сводится к следующему.
сводится к следующему.
В графе 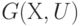 находят вершину
находят вершину  с минимальной локальной степенью
с минимальной локальной степенью  .
.
Если таких вершин несколько, то предпочтение отдаётся той вершине, которая имеет большее число кратных рёбер. С этой вершины начинается построение первого куска.
С этой целью в 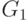 первоначально включаются
первоначально включаются 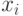 и все вершины, смежные ей.
Обозначим это множество
и все вершины, смежные ей.
Обозначим это множество  .
.
Если полученное число вершин равно " 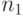 ", то считаем, что кусок
", то считаем, что кусок  образован.
образован.
Если это число больше " 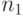 " , то удаляем "лишние" вершины,
связанные с остающимися вершинами
" , то удаляем "лишние" вершины,
связанные с остающимися вершинами 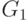 меньшим числом рёбер.
меньшим числом рёбер.
В случае, когда мощность множества 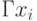 меньше "
меньше " 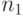 " ,
то из
" ,
то из  выбирается вершина, удовлетворяющая условию
выбирается вершина, удовлетворяющая условию
 |
( 19.7) |
где  - число рёбер, соединяющих вершину
- число рёбер, соединяющих вершину  со всеми невыбранными вершинами.
со всеми невыбранными вершинами.
Строим множество вершин  смежных
смежных 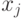 ,
и процесс выборки вершин
,
и процесс выборки вершин  повторяется. Образованный подграф
повторяется. Образованный подграф  исключаем из исходного графа.
исключаем из исходного графа.
Далее в графе 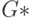 выбирается вершина с минимальной локальной степенью. Производится её помещение в G_{ 2 }, и процесс повторяется до тех пор, пока граф
выбирается вершина с минимальной локальной степенью. Производится её помещение в G_{ 2 }, и процесс повторяется до тех пор, пока граф  не будет разрезан на "l" частей.
не будет разрезан на "l" частей.
Описанный алгоритм прост, позволяет быстро получать результаты разбиения, однако в общем случае может привести к неоптимальным результатам. Наибольшая эффективность данного метода последовательного разбиения графа  значительно больше числа вершин в любой части разбиения, т.е.
значительно больше числа вершин в любой части разбиения, т.е.

Рассмотрим принципиальную электрическую схему RC - генератора, рис. 19.1.
Обозначим условно элементы схемы через  .
Представим эту схему в виде произвольного неориентированного графа
.
Представим эту схему в виде произвольного неориентированного графа 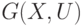 ,
у которого
,
у которого  , а
, а  - множество электрических связей элементов конструкции рис. 19.2.
На этом рисунке клеммы схемы обозначены через
- множество электрических связей элементов конструкции рис. 19.2.
На этом рисунке клеммы схемы обозначены через  , соответственно.
, соответственно.
По исходному графу составляем матрицу смежности, 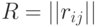 ,
где
,
где 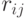 - элемент матрицы, состоящий из пересечения
- элемент матрицы, состоящий из пересечения  -ой строки и
-ой строки и  -го столбца. Строки и столбцы матрицы смежности соответствуют вершинам графа,
а ее
-го столбца. Строки и столбцы матрицы смежности соответствуют вершинам графа,
а ее 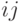 -ый элемент равен числу кратных ребер, связывающих вершины
-ый элемент равен числу кратных ребер, связывающих вершины 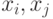 .
Матрица смежности
.
Матрица смежности  неориентированного графа всегда симметрична.
неориентированного графа всегда симметрична.

|

|
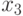
|
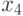
|
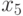
|

|

|
||
|---|---|---|---|---|---|---|---|---|

|
0 | 0 | 1 | 0 | 0 | 0 | 0 | |

|
0 | 0 | 1 | 2 | 0 | 0 | 0 | |
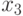
|
1 | 1 | 0 | 2 | 1 | 0 | 0 | |
| R= | 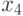
|
0 | 2 | 2 | 0 | 0 | 1 | 0 |
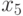
|
0 | 0 | 1 | 0 | 0 | 1 | 0 | |

|
0 | 0 | 0 | 1 | 1 | 0 | 1 | |

|
0 | 0 | 0 | 0 | 0 | 1 | 0 | |
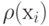
|
 |
 |
 |
 |
 |
 |
 |
Суммируя элементы столбцов матрицы "  ", вычислим локальную степень каждой вершины
", вычислим локальную степень каждой вершины 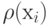 . Полученные результаты запишем в нижнюю строку матрицы.
. Полученные результаты запишем в нижнюю строку матрицы.
Пусть, граф, изображённый на рис. 19.2, надо разбить на три куска с количеством вершин 3, 2, и 2 в каждом куске, соответственно. Эти условия в данной задаче будут ограничениями. Целью разбиения является получение минимального количества внешних связей, т.е. ребер, связывающих куски графа между собой.
Находим вершину 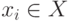 с максимальной локальной степенью,
которая определяется из матрицы смежности.
Эта и все связанные с ней вершины помещаются в первый кусок
с максимальной локальной степенью,
которая определяется из матрицы смежности.
Эта и все связанные с ней вершины помещаются в первый кусок  .
В нашем случае это вершины:
.
В нашем случае это вершины:  ,
,  .
Пусть, с
.
Пусть, с 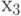 начнётся образование куска
начнётся образование куска  .
В него помещается
.
В него помещается 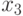 и все вершины, смежные с ней.
Так как с
и все вершины, смежные с ней.
Так как с 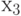 связаны
связаны 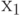 ,
, 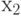 ,
, 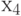 и
и  ,
то вершины, имеющие меньшее число связей с куском
,
то вершины, имеющие меньшее число связей с куском  (это
(это  и
и 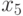 ), исключаются (рис. 19.3). Получился граф
), исключаются (рис. 19.3). Получился граф  ,
где
,
где 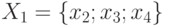 . Оставшуюся часть обозначают следующим образом:
. Оставшуюся часть обозначают следующим образом:  , где
, где 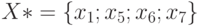 .
Построим граф
.
Построим граф 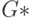 (рис. 19.4) и матрицу смежности для него (табл. 19.2).
(рис. 19.4) и матрицу смежности для него (табл. 19.2).
Определим локальную степень вершины по матрице смежности

Максимальную локальную степень имеет вершина 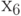 ,
поместим ее и все связанные с ней вершины в кусок
,
поместим ее и все связанные с ней вершины в кусок 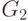 .
Так как в нём должно быть две вершины, то
.
Так как в нём должно быть две вершины, то  исключаем. В результате будет следующее разбиение:
исключаем. В результате будет следующее разбиение:
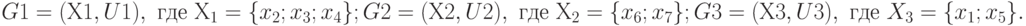
Окончательное разбиение графа приведено на рис. 19.5.
Рассчитаем коэффициент разбиения по формуле. Имеется четыре внешних и шесть внутренних связей вершин. Следовательно, коэффициент разбиения графа

Недостатком этих алгоритмов является получение результатов, которые в общем случае могут быть далеки от оптимальных, что сужает область их использования. Для улучшения разбиения используются итерационные алгоритмы.

 где
где 
 .
.