НОУ ИНТУИТ | Моделирование систем. Лекция 4: Выборочный метод Монте-Карло

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Мордовский государственный университет имени Н.П. Огарева

Опубликован: 30.11.2010 | Доступ: свободный | Студентов: 3284 / 1985 | Оценка: 4.12 / 4.13 | Длительность: 14:37:00

ISBN: 978-5-9963-0352-6

Темы: Программирование, Алгоритмы и дискретные структуры

Специальности: Программист, Системный архитектор

|

Вам нравится? Нравится 31 студенту

| Поделиться |

Поддержать курс

| Скачать электронную книгу

Практическая часть

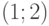Пример 1. Рассчитайте с помощью метода Монте-Карло площадь круга радиусом r = 5 и с координатами центра (1; 2) . Число испытаний примите 500. Выполните графические построения, поясняющие расчет.

Для определения площади плоской фигуры ее вписывают в соответствующую известную фигуру, площадь которой достаточно просто вычисляется. Вычисление площади круга может быть произведено через вычисление площади квадрата, в который вписывается круг. Выборочный метод Монте-Карло предполагает генерирование случайных (псевдослучайных) равномерно распределенных чисел. Этим числам сопоставляются координаты точек для рассматриваемой фигуры — квадрата, в которую вписывается круг. Если площадь квадрата подсчитана, то задается число испытаний , из которых исходов могут оказаться внутри круга или на его границе, т. е. на окружности. Тогда площадь круга 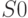будет определяться выражением

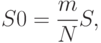
$S0=\frac{m}{N}S,$

где:

— число сгенерированных случайных чисел, соответствующих количеству точек, находящихся в данном квадрате:

— число случайных чисел (точек), которые попали в круг. Граница круга — это окружность, уравнение которой имеет вид

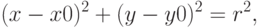
где:

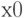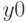, — координаты центра окружности;

, — текущие значения переменных;

— радиус окружности.

Программный код решения примера:

clear all, clc,close all
%%%%%%% Расчет площади круга методом Монте-Карло
%% Параметры
r = 5;
x0 = 1;
y0 = 2;
%%% Построение окружности
t = 0 : r/500 : 2*pi;
x = r*cos(t) + x0;
y = r*sin(t) + y0;
line(x, y, 'linew', 2, 'color','r')
%%% Центр круга
line(x0,y0,'marker','o','markerfacecolor','r','color', 'r' )
 
%%% Построение квадрата, в который вписан круг
line([x0-r, x0+r],[y0+r, y0+r], 'lines','-.')
line([x0-r, x0+r],[y0-r, y0-r], 'lines','-.')
line([x0+r, x0+r],[y0-r, y0+r], 'lines','-.')
line([x0-r, x0-r],[y0-r, y0+r],  'lines','-.')
 
%%% Гененрирование случайных чисел для области D*
N = 500; %%% число испытаний
%%% Генерация чисел по горизонтальной стороне квадрата
rx = min(x) + (max(x) - min(x))*rand(N,1);
%%% Генерация чисел по вертикальной стороне квадрата
ry = min(y) + (max(y) - min(y))*rand(N,1);
%%%% Заполнение случайными числами квадрата с кругом
for J = 1 : N
line(rx(J),ry(J),'marker','o','markersize',2,'color', 'k',...
 'markerfacecolor', 'k' )
end
%%% Подсчет количества случайных чисел, попавших в круг
m = 0;
for J = 1 : N
    if (rx(J) - x0)^2 + (ry(J) - y0)^2 <= r^2
        m = m + 1;
    end
end
%%%%% Расчет площади квадрата
S = ((x0+r) - (x0-r))^2;
 
%%% Расчет площади круга методом Монте-Карло
S0 = m/N*S

%%% Проверка расчета 
Scontrol = pi*r^2

%%% Заголовок для диаграммы
str = sprintf('%s Радиус круга r = %g, координаты центра x_0 = %g,  y_0 = %g.%s%g%s%g. %s%g', '\bf',r,x0,y0, ... 
'\newline Теоретическая площадь круга S = ', Scontrol, ...
'\newline Площадь круга по методу Монте-Карло S0 = ', S0, ...
 'Число испытаний N = ', N);
title(str)
grid on
xlabel('\bf - - - - - - - X  - - - - - - - ')
ylabel('\bf - - - - - - - Y  - - - - - - - ')
%%% Ограничения по осям
xlim([x0 - r - r/10, x0 + r + r/10])
ylim([y0 - r - r/10, y0 + r + r/10])
axis equal

Задание 1

Видоизмените программу так, чтобы выполнялось условие непревышения относительной погрешности заданной величины (например, 1%) и чтобы производился необходимый подсчет числа испытаний.
Предусмотрите, чтобы точки, попавшие в круг, были красного цвета, а не попавшие в него – синего цвета.
Напишите программу расчета числа $\pi$ по методу Монте-Карло. Расчет числа $\pi$ произведите с точностью в четыре знака после десятичной точки.

Пример 2. Рассчитайте с помощью метода Монте-Карло площадь фигуры, ограниченной эллипсом с большой осью 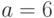a = 6 и малой осью 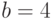b = 4 . Координаты пересечения осей эллипса 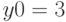x0 = –2 , y0 = 3 , оси коллинеарны декартовым осям.

Теоретическая площадь эллипса вычисляется по формуле

$S=\pi ab,$

где:

— большая ось эллипса;

— малая ось эллипса.

Каноническое уравнение эллипса (относительно центра координат):

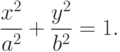
$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1.$

Программный код решения примера:

clear all, clc, close all
%%%% Расчет площади эллипса методом Монте-Карло
%%% Параметры эллипса
a = 6;
b = 4;
x0 = -2;
y0 = 3;

%%% Построение эллипса
t = 0 : min([a, b])/500 : 2*pi;
x = a*cos(t) + x0;
y = b*sin(t) + y0;
line(x,y, 'linew', 2, 'color', [1,0,0])
%%% Центр пересечения осей эллипса
line(x0,y0,'marker','o','markerfacecolor','r','color','r' )
 
%%% Построение прямоугольника, в который вписан эллипс
line([x0-a, x0+a],[y0+b,y0+b], 'lines','-.')
line([x0-a, x0+a],[y0-b,y0-b], 'lines','-.')
line([x0-a, x0-a],[y0-b,y0+b], 'lines','-.')
line([x0+a, x0+a],[y0-b,y0+b], 'lines','-.')
 
%%% Гененрирование случайных чисел для области D* - области прямоугольника
N = 500; %%% число испытаний
%%% Генерация чисел по горизонтальной стороне прямоугольника
rx = (x0-a) + (x0+a - (x0-a))*rand(N,1);
%%% Генерация чисел по вертикальной стороне прямоугольника
ry = (y0-b) + (y0+b - (y0-b))*rand(N,1);

%%%% Заполнение случайными числами прямоугольника с эллипсом
for J = 1 : N
line(rx(J),ry(J),'marker','o','markersize',2,'color', 'k',...
 'markerfacecolor', 'k' )
end
 
%%% Подсчет количества случайных чисел, попавших в эллипс
m = 0;
for J = 1 : N
    if ((rx(J) - x0)/a)^2 + ((ry(J) - y0)/b)^2 <= 1
        m = m + 1;
    end
end
 
%%%%% Расчет площади прямоугольника
S = ((x0+a) - (x0-a))*((y0+b)-(y0-b));
 
%%% Расчет площади эллипса методом Монте-Карло
S0 = m/N*S
 
%%% Проверка расчета 
Scontrol = pi*a*b
 
%%% Заголовок для диаграммы
str = sprintf('%s Оси эллипса a = %g, b = %g, координаты центра x_0 = %g,  y_0 = %g.%s%g%s%g. %s%g', '\bf',a, b,x0,y0, ... 
'\newline Теоретическая площадь эллипса S = ', Scontrol, ...
'\newline Площадь эллипса по методу Монте-Карло S0 = ', S0, ...
 'Число испытаний N = ', N);
title(str)
grid off %% выключение сетки на диаграмме
xlabel('\bf - - - - - - - X  - - - - - - - ')
ylabel('\bf - - - - - - - Y  - - - - - - - ')
%%% Установление размеров и свойств графического окна
gfig = get(0, 'screensize');
set(gcf, 'color', 'w', 'position', [gfig(1) + 100, gfig(2) + 100, gfig(3)*0.8, gfig(4)*0.7])
%%% Ограничения по осям
xlim([x0-a-a/10, x0+a+a/10])
ylim([y0-b-b/10, y0+b+b/10])
axis equal

Задание 2

Для построения эллипса используйте его каноническое уравнение.
Предусмотрите, чтобы точки, попавшие в эллипс, были красного цвета, а не попавшие в него — синего цвета.
Координаты центра пересечения осей эллипса примите случайными при использовании функции .
Оси эллипса примите случайными, равномерно распределенными из интервала , где — номер компьютера, за которым выполняется лабораторная работа ( .).
В программу включите расчет общего числа испытаний, при котором достигается заданная относительная погрешность в 2%.
В программу включите построение графика относительной погрешности от числа испытаний начиная с 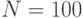и более.

Пример 3. Найдите оценку значения тройного интеграла методом Монте-Карло

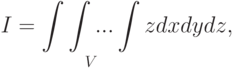
$I=\mathop{{\int\int ... \int}}\limits_{V}zdxdydz,$

где — область, ограниченная круговым конусом $z^2=\frac{h^2}{R^2}(x^2+y^2)$ и плоскостью z = h , h = 5 , R = 2 .

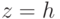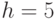Программный код решения примера:

clear all, clc, close all
%%% Вычисление тройного интеграла методом Монте-Карло, 
R = 2;
h = 5;

%%% Для построения конуса
[x,y] = meshgrid(-1.2*R:0.02:1.2*R, -1.2*R:0.02:1.2*R);
z = h/R*sqrt(x.^2 + y.^2);
xmax = 1.2*R;
%% Радиус окружности в сечении конуса на высоте max(z)
rmax = sqrt(xmax^2 + xmax^2);
%%% Максимальное значение аппликаты
zmax = h/R*sqrt(xmax^2 + xmax^2);
%%% Тангенс угла фронтального сечения конуса
koef = (rmax/zmax);
%%% Радиус окружности в сечении конуса на высоте h
rh = h*(koef); 
 
%%% Круговой конус
mesh(x,y,z) %% функция построения пространственных фигур
hold on
%%% Плоскость на высоте h
line(x, y, h*ones(size(x)))
 
%%% Параллелепипед 
line([-rh, rh],[-rh,-rh],[0,0])
line([-rh, -rh],[-rh,-rh],[0,h])
line([rh, rh],[-rh,-rh],[0,h])
 
line([-rh, rh],[rh,rh],[0,0])
line([-rh, -rh],[rh,rh],[0,h])
line([rh, rh],[rh,rh],[0,h])
 
line([-rh, -rh],[-rh,rh],[0,0])
line([rh, rh],[-rh,rh],[0,0])
 
%%% Вычисление тройного интеграла по встроенным функциям int
syms x y z
In0 = int(int(int(z, z, h/R*sqrt(x^2+y^2), h), ...
    y, -sqrt(rh^2 - x^2), sqrt(rh^2 - x^2)), x, -rh, rh);
In = double(In0)
%%% Расчет тройного интеграла методом Монте-Карло
N = 1000; %%% Число испытаний
S = 0;
for J = 1 : N
    xr = -rh + (rh - (-rh))*rand;
    yr = -rh + (rh - (-rh))*rand ;
    zr = h*rand;
if  zr^2<=h^2/R^2*(xr^2 + yr^2) & h/R*sqrt(xr^2 + yr^2)>=0 & ... 
         h/R*sqrt(xr^2 + yr^2) <= h 
 
        S = S + zr; 
      end
end
 
mD = [2*rh]*[2*rh]*[h]; %%% Объем параллелепипеда, мера
In_Car = (mD/N)*S
 
grid on
str = sprintf('%s%g;%s Точное значение тройного интеграла: %g',...
    '\bf Значение интеграла по методу Монте-Карло: ', In_Car, '\newline', In);
title(str)
 
view(-30,20)
axis equal

Задание 3

Формирование случайных переменных 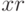, , 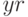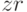вынесите за пределы цикла.
Объясните расстановку пределов интегрирования.
Вычислите по методу Монте-Карло объем тела для полученных пределов интегрирования. Сравните со значением, вычисленным аналитически.

Задание 4

В нижеприводимых заданиях выполните графические построения заданных плоских фигур и напишите программы по расчету площадей этих фигур в системе MATLAB.

Рассчитайте с помощью метода Монте-Карло площадь фигуры, ограниченной гипоциклоидой с параметрами ; ; 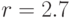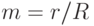. Параметрическое уравнение гипоциклоиды: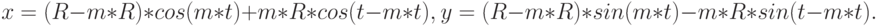

$x =(R-m*R)*cos(m*t)+m*R*cos(t-m*t),\\ y = (R-m*R)*sin(m*t)-m*R*sin(t-m*t).$

Подберите массив значений параметра .

Относительная погрешность расчета не должна превышать 5%.
Рассчитайте с помощью метода Монте-Карло площадь фигуры, ограниченной кривой Штейнера с параметром . Параметрическое уравнение кривой Штейнера:

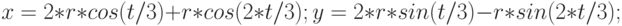
$x = 2*r*cos(t/3) + r*cos(2*t/3);\\ y = 2*r*sin(t/3) - r*sin(2*t/3);$

Подберите массив значений параметра .

Относительная погрешность расчета не должна превышать 5%.
Рассчитайте с помощью метода Монте-Карло площадь фигуры, ограниченной астроидой с параметром . Параметрическое уравнение астроиды:

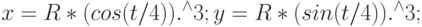
$x = R*(cos(t/4)).^{\wedge} 3;\\ y = R*(sin(t/4)).^{\wedge} 3;$

Подберите массив значений параметра .

Относительная погрешность расчета не должна превышать 5%.

Задание 5

В нижеприводимых заданиях выполните графические построения заданных пространственных тел и напишите программы по вычислению объемов этих тел в системе MATLAB.

Вычислите с помощью метода Монте-Карло объем тела, ограниченного параболоидом $\frac{y^2}{4}+\frac{z^2}{9}=2\frac{x}{3}$ и плоскостью .

Относительная погрешность расчета не должна превышать 5%.
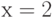Вычислите с помощью метода Монте-Карло объем тела, ограниченного поверхностями:

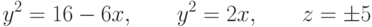
$y^2=16-6x,\qquad y^2=2x,\qquad z=\pm 5$

Относительная погрешность расчета не должна превышать 5%.
С помощью метода Монте-Карло вычислите объем тела, ограниченного поверхностями 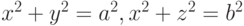$x^{2}+y^{2}=a^{2}, x^{2}+z^{2}=b^{2}$ и 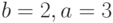(рассмотреть ту из областей внутри конуса, для которой $х \ge 0$ ).

Относительная погрешность расчета не должна превышать 5%.

Контрольные вопросы

Какой закон распределения случайной величины используется при вычислении кратных интегралов методом Монте-Карло?
Чему равен интегрант трехкратного интеграла при вычислении объема тел методом Монте-Карло?
От чего зависит точность метода Монте-Карло?
Как определяется оценка "исправленного" среднеквадратического отклонения?

Дальше >>

Авторизоваться

Моделирование систем

Выборочный метод Монте-Карло

Практическая часть

Контрольные вопросы

Вопросы и ответы