|
Так это же динамическое программирование на основе математической индукции. |
Задача ГП без ограничений: двойственность
Двойственная задача
Теория двойственности для задач линейного программирования обязательно изучается в курсах, посвященных решению экстремальных задач. Однако и для любой задачи нелинейного программирования, частным случаем которой является задача ГП, можно указать некоторую другую задачу, которая называется двойственной по отношению к исходной (прямой) задаче. Основная идея двойственности состоит в том, что при некоторых предположениях о свойствах прямой задачи равны оптимальные значения целевых функций прямой и двойственной задач. Это дает возможность получить решение прямой задачи, решив двойственную задачу.
Рассмотрим определенную в "Задача ГП без ограничений" задачу ГП без ограничений:
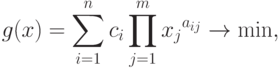 |
( 32) |
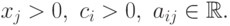
Двойственной задачей для задачи (32) называется следующая задача:
 |
( 33) |
при ограничениях
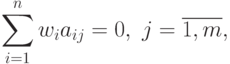 |
( 34) |
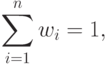 |
( 35) |
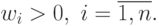 |
( 36) |
Функция  называется двойственной функцией для функции
называется двойственной функцией для функции  , переменные
, переменные 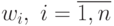 называются двойственными переменными. Ограничения (34)
называются условиями ортогональности, ограничение
(35) называется условием нормальности.
называются двойственными переменными. Ограничения (34)
называются условиями ортогональности, ограничение
(35) называется условием нормальности.
Систему ограничений (34)--(35) можно записать в матричном виде. Здесь и далее будем использовать матричную форму записи, принятую в теории двойственности: вектор двойственных переменных - левый элемент умножения, матрица ограничений - правый. Тогда получим формулу
 |
( 37) |
где 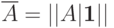 ,\
,\ 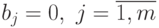 ,\
,\ 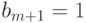 .
.
Прямая и двойственная задачи связаны следующей теоремой, доказательство которой имеется, например, в [5]:
Теорема 7 (теорема двойственности) Если задача (32) разрешима и достигает своего минимума
в точке 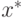 , то двойственная задача (33) также
разрешима и
достигает своего максимума в некоторой точке
, то двойственная задача (33) также
разрешима и
достигает своего максимума в некоторой точке 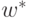 . При этом выполняются
следующие равенства:
. При этом выполняются
следующие равенства:
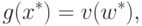 |
( 38) |
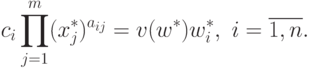 |
( 39) |
Из теоремы двойственности следует, что для нахождения оптимального решения прямой задачи ГП можно попытаться сначала найти оптимальное решение двойственной задачи. Если решение двойственной задачи существует, то оптимальное решение прямой задачи удовлетворяет уравнениям (39). В противном случае прямая задача не имеет оптимального решения.
Такой подход особенно просто реализовать, когда двойственная задача имеет единственное допустимое решение, которое, естественно, будет и оптимальным. Приведем примеры.
Пример 27 Докажем, используя теорему двойственности, что следующая задача ГП
не имеет оптимального решения:
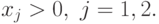
Определим сначала двойственную функцию для позинома  ,
используя формулу (33).
Позином состоит из трех мономов, следовательно, двойственная
функция имеет три переменные:
,
используя формулу (33).
Позином состоит из трех мономов, следовательно, двойственная
функция имеет три переменные: 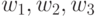 . Вектор
коэффициентов позинома
. Вектор
коэффициентов позинома 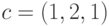 . Следовательно,
двойственная функция для позинома
. Следовательно,
двойственная функция для позинома  имеет вид:
имеет вид:
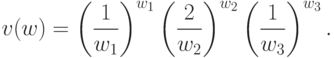
Запишем теперь условия ортогональности для позинома (формулы (34)).
Поскольку в позином  входят две переменные
входят две переменные 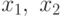 , то условия
ортогональности состоят из двух равенств. Матрица экспонент
позинома
, то условия
ортогональности состоят из двух равенств. Матрица экспонент
позинома 
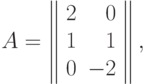
где  -й столбец образован показателями степеней при
-й столбец образован показателями степеней при  -й
переменной
-й
переменной 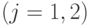 . По формуле (34) условия
ортогональности для позинома
. По формуле (34) условия
ортогональности для позинома  имеют вид:
имеют вид:
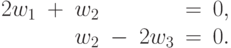 |
( 40) |
Запишем условие нормальности (формулы (35)):

Таким образом, двойственная задача имеет вид:
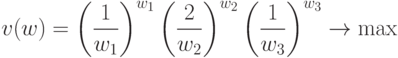
при ограничениях
 |
( 41) |
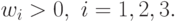
Cистема линейных уравнений (41) имеет единственное
решение:  ,
,  ,
, 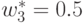 ,
которое не удовлетворяет условию (36):
,
которое не удовлетворяет условию (36):  . Это означает, что не существует допустимого решения
двойственной задачи, следовательно, не существует и оптимального
решения этой задачи. Из теоремы двойственности следует, что в
этом случае прямая задача ГП не имеет оптимального решения.
. Это означает, что не существует допустимого решения
двойственной задачи, следовательно, не существует и оптимального
решения этой задачи. Из теоремы двойственности следует, что в
этом случае прямая задача ГП не имеет оптимального решения.
Пример 28 Решим следующую задачу ГП, используя теорему двойственности: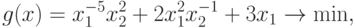
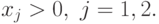
Определим сначала двойственную функцию для позинома  .
Позином состоит из трех мономов, следовательно, двойственная
функция имеет три переменные:
.
Позином состоит из трех мономов, следовательно, двойственная
функция имеет три переменные: 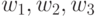 . Вектор коэффициентов позинома
. Вектор коэффициентов позинома 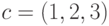 . Следовательно, двойственная функция для позинома
. Следовательно, двойственная функция для позинома  имеет вид:
имеет вид:
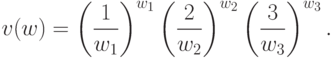
Запишем теперь условия ортогональности для позинома. Поскольку в позином  входят две переменные
входят две переменные 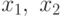 , то условия
ортогональности состоят из двух равенств. Матрица экспонент
позинома
, то условия
ортогональности состоят из двух равенств. Матрица экспонент
позинома 
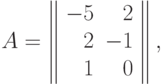
где  -й столбец образован показателями степеней при
-й столбец образован показателями степеней при  -й
переменной
-й
переменной 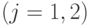 . По формуле (34) условия
ортогональности для позинома
. По формуле (34) условия
ортогональности для позинома  имеют вид:
имеют вид:
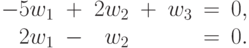 |
( 42) |
Запишем условие нормальности (формула (35)):

Таким образом, двойственная задача имеет вид:
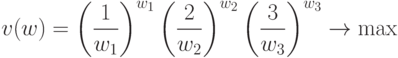
при ограничениях
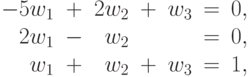 |
( 43) |
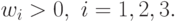
Так как система линейных уравнений (43) имеет
единственное решение: 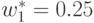 ,
, 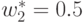 ,
, 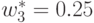 и оно удовлетворяет условию
и оно удовлетворяет условию  , то это оптимальное решение двойственной
задачи. Теперь мы можем вычислить оптимальное значение
двойственной функции. Ограничим точность вычисления значения
, то это оптимальное решение двойственной
задачи. Теперь мы можем вычислить оптимальное значение
двойственной функции. Ограничим точность вычисления значения 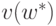 и наших дальнейших вычислений двумя знаками после
запятой:
и наших дальнейших вычислений двумя знаками после
запятой:
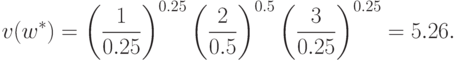
Согласно теореме двойственности
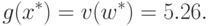
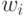 показывают, каков вклад монома
показывают, каков вклад монома  в
минимальное значение целевой функции
в
минимальное значение целевой функции 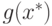 . Следовательно, вклад первого
монома в целевую функцию составляет
. Следовательно, вклад первого
монома в целевую функцию составляет 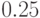 , вклад второго -
, вклад второго - 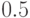 ,
а вклад третьего -
,
а вклад третьего - 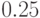 .
.Осталось определить оптимальное решение прямой задачи. Используем для этого формулы (39) из теоремы двойственности. Требуется решить нелинейную систему из трех уравнений с двумя неизвестными:
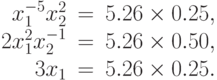 |
( 44) |
Из третьего уравнения системы (44) находим, что 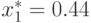 .
Из второго уравнения получаем, что
.
Из второго уравнения получаем, что 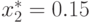 .
Не должен удивлять тот факт, что при нахождении решения системы (44)
не использовалось первое уравнение системы. Это объясняется тем,
что в этой системе одно из уравнений (любое) является избыточным.
.
Не должен удивлять тот факт, что при нахождении решения системы (44)
не использовалось первое уравнение системы. Это объясняется тем,
что в этой системе одно из уравнений (любое) является избыточным.
В качестве следующего примера рассмотрим классическую задачу управления запасами. Мы покажем, что эта задача является задачей ГП, а известная формула для оптимального размера заказа может быть получена из решения двойственной задачи.
