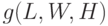|
Так это же динамическое программирование на основе математической индукции. |
Задача ГП без ограничений: двойственность
Простейшая задача управления запасами
Для обеспечения непрерывности производственного процесса необходимо поддерживать достаточный запас материальных ресурсов. При этом достаточность понимается, как компромисс между двумя крайними стратегиями, когда слишком низкий уровень запасов приводит к остановке производства, а слишком высокий - к непомерным расходам на хранение.
В классических моделях принято характеризовать запас неизбежными издержками на выполнение выбранной стратегии его пополнения. Мы рассмотрим задачу управления запасами в следующих предположениях: спрос на запасаемый продукт постоянен во времени; заказ выполняется мгновенно; дефицит не допускается.
Мы рассмотрим случай, когда общие затраты на управление запасами состоят из затрат на оформление заказов и затрат на их хранение. Введем следующие обозначения:
-
 - спрос на запас (в единицу времени);
- спрос на запас (в единицу времени); -
 - затраты на оформление заказа (не зависят от его объема);
- затраты на оформление заказа (не зависят от его объема); -
 - затраты на хранение единицы складируемой продукции (в единицу времени).
- затраты на хранение единицы складируемой продукции (в единицу времени).
В сделанных предположениях стратегия управления запасами будет
определяться двумя величинами: объемом заказа  и временем
между двумя последовательными заказами
и временем
между двумя последовательными заказами  . Так как предполагается
равномерный расход запаса, то
. Так как предполагается
равномерный расход запаса, то
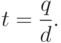 |
( 45) |
Так как средний уровень запаса равен  ,
то затраты на хранение вычисляются по формуле:
,
то затраты на хранение вычисляются по формуле:
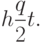
Используя введенные обозначения и формулу (45), напишем
формулу для величины общих затрат 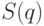 в единицу времени:
в единицу времени:
 |
( 46) |
Естественно определить величину заказа  , при которой значение
функции
, при которой значение
функции 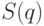 минимально. Так как из формулы (46)
следует, что функция
минимально. Так как из формулы (46)
следует, что функция 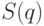 является позиномом, то мы используем
для вычисления ее минимального значения теорему двойственности.
является позиномом, то мы используем
для вычисления ее минимального значения теорему двойственности.
Определим сначала двойственную функцию для позинома 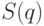 .
Позином состоит из двух мономов, следовательно, двойственная
функция имеет две переменные. Вектор коэффициентов позинома
.
Позином состоит из двух мономов, следовательно, двойственная
функция имеет две переменные. Вектор коэффициентов позинома 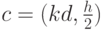 . Следовательно, двойственная функция для позинома
. Следовательно, двойственная функция для позинома 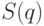 имеет вид:
имеет вид:

Запишем теперь условия ортогональности для позинома. Поскольку в
позином 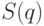 входит одна переменная
входит одна переменная  , то условия
ортогональности состоят из одного равенства. В равенстве два
слагаемых, поскольку в позиноме два монома. Матрица экспонент
позинома
, то условия
ортогональности состоят из одного равенства. В равенстве два
слагаемых, поскольку в позиноме два монома. Матрица экспонент
позинома 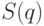
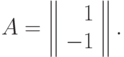
По формуле (34) условие ортогональности для
позинома 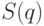 имеет вид:
имеет вид:
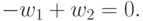
Запишем условие нормальности (формула (35)):

Таким образом, двойственная задача имеет вид:
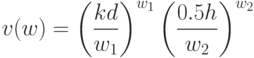
при ограничениях
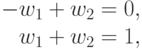 |
( 47) |
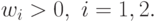
Так как система линейных уравнений (47) имеет единственное
решение: 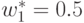 ,
, 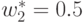 и оно удовлетворяет
условию
и оно удовлетворяет
условию 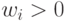
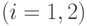 , то это оптимальное решение
двойственной задачи. Теперь мы можем вычислить оптимальное
значение двойственной функции:
, то это оптимальное решение
двойственной задачи. Теперь мы можем вычислить оптимальное
значение двойственной функции:
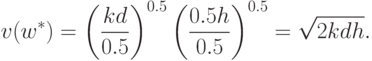
Согласно теореме двойственности
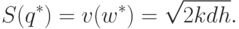
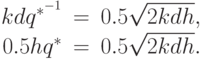
Из любого уравнения находим, что 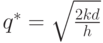 \ (одно из уравнений
является избыточным).
\ (одно из уравнений
является избыточным).
Степень трудности задачи ГП
Степень трудности задачи геометрического программирования (Degree of Difficulty или, сокращенно, DOD) определяется по формуле:
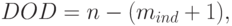 |
( 48) |
где  - число мономов в позиноме,
- число мономов в позиноме, 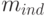 - число независимых переменных (определяемое рангом матрицы
- число независимых переменных (определяемое рангом матрицы 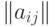 ).
).
Пример 13 (продолжение) Вычислим степень трудности для задачи ГП:
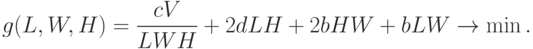
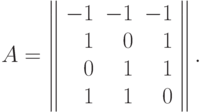
Здесь 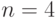 ,
,  , поэтому
, поэтому  .
.
Пример 14 (продолжение). Вычислим степень трудности для задачи ГП:
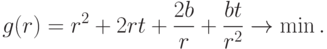

Здесь 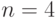 ,
, 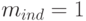 , поэтому
, поэтому  .
.
Пример 29 Вычислим степень трудности для задачи ГП и запишем матрицу системы уравнений двойственной задачи из примера 28.
Вычислим степень трудности для задачи ГП:
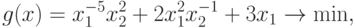
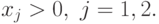
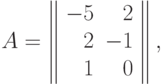
Здесь 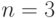 ,
,  , поэтому
, поэтому  .
Система ограничений двойственной задачи имеет вид:
.
Система ограничений двойственной задачи имеет вид:
 |
( 49) |
Матрица системы ограничений двойственной задачи (формула (37)) имеет вид:
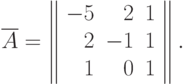
Заметим, что все столбцы этой матрицы линейно независимы. Таким образом, система (49) однозначно разрешима.
Для того, чтобы система уравнений {(34)}--{(35)} была однозначно разрешима, необходимо и достаточно, чтобы степень трудности задачи ГП была равна нулю. Если степень трудности больше нуля, то система {(34)}--{(35)} разрешима, но имеет не единственное решение. Двойственная задача в этом случае может быть переформулирована в терминах базисных переменных, число которых совпадает со степенью трудности задачи ГП.
Использование теоремы двойственности
Покажем на примерах, как в ряде случаев можно использовать теорему двойственности для решения задач ГП.
Решение задачи ГП при DOD=0
Вернемся к задаче о перевозке груза из лекции 2.
Пример 13 (продолжение) Решим задачу ГП:
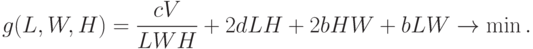
Двойственная задача имеет вид:
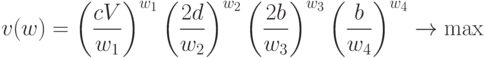
при ограничениях
 |
( 50) |

Степень трудности задачи ГП равна нулю (столбцы и строки матрицы системы уравнений линейно независимы), следовательно, система (50) разрешима и имеет единственное решение:
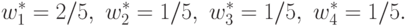
Поскольку выполняется условие 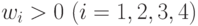 , то это оптимальное решение двойственной задачи. Теперь мы можем
вычислить оптимальное значение двойственной функции:
, то это оптимальное решение двойственной задачи. Теперь мы можем
вычислить оптимальное значение двойственной функции:
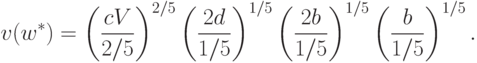
Рассмотрим численный пример. Пусть 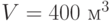 ,
, 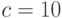 руб.,
руб., 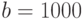 руб.,
руб.,  руб.
Вычислим значение двойственной функции при этих значениях параметров:
руб.
Вычислим значение двойственной функции при этих значениях параметров:
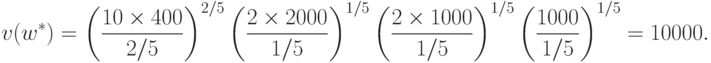
По теореме двойственности 7выполняется следующее равенство:

Вычислим теперь оптимальные значения переменных  ,
,  ,
,  ,
используя формулы (39):
,
используя формулы (39):
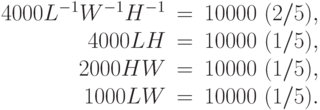
Упростив, получим систему уравнений:
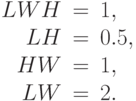
Решим систему, используя общий подход к решению такого рода
нелинейных систем. Прологарифмируем каждое уравнение и выполним
замену переменных  ,
, 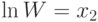 ,
, 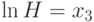 .
.
Получим следующую систему линейных уравнений:
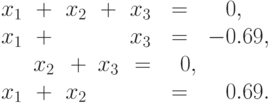
Решая ее, находим  ,
, 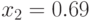 ,
, 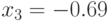 .
Выполнив обратную замену
.
Выполнив обратную замену  ,
, 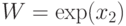 ,
,  , получаем оптимальные размеры контейнера:
, получаем оптимальные размеры контейнера: 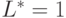 ,
, 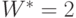 ,
,  .
.