Модель процесса изготовления в цехе деталей

Решение обратной задачи

Целью обратной задачи является определение среднего времени на изготовление какого-то количества деталей. Для проверки работоспособности модели возьмём количество деталей, полученных в результате решения прямой задачи, т.е. Det = 9.

Особенности построения программы модели

Модель для решения обратной задачи приведена ниже.

; Модель процесса изготовления деталей. Обратная задача

…

;  Имитация выполнения 3-й операции
  ASSIGN    2,3  ; Код 3 в Р2-признак 3-й операции
Oper3  QUEUE  P2        ; Встать в очередь
  SEIZE    Konveer3  ; Начать третью операцию
  DEPART    P2        ; Покинуть очередь
  ADVANCE    (Exponential (23,0,T3)) ; 3-я операция
  RELEASE    Konveer3    ; Закончить 3-ю операцию
  ADVANCE    (Exponential (23,0,Tk3)); Контроль 3-й операции
  TRANSFER  q3_,,Sboi   ; Брак на пункт контроля
  TRANSFER  ,Met2      ; Готовые детали
; Сегмент имитации работы пункта контроля
Sboi  QUEUE    Kont      ; В очередь на пункт контроля
  SEIZE    Kontr    ; Занять пункт контроля
  DEPART    Kont      ; Покинуть очередь на пункт контроля
  ADVANCE    (Exponential(23,0,Tk)); Окончательный контроль
  RELEASE    Kontr    ; Освободить пункт контроля
  TRANSFER  q4_,,EndOper  ; В окончательный брак
  TEST E    P1,1,EndOper  ; Если второй раз, то в окончательный брак
  ASSIGN    1,2  ; Код 2 в Р1-деталь пойдёт второй раз
Met1  TRANSFER  ,(Met1+P2)
  TRANSFER  ,Oper1    ; Повторно на 1-ю операцию
  TRANSFER  ,Oper2    ; Повторно на 2-ю операцию
  TRANSFER  ,Oper3    ; Повторно на 3-ю операцию
EndOper  TERMINATE    ; Счет брака
; Сегмент завершения моделирования и расчета результатов
Met2  TEST L  X$Prog,TG1,Met3  ; Если условие выполняется, то
  SAVEVALUE Prog,TG1    ; X$Prog=TG1 счетчику завершений
Met3  SAVEVALUE  NDet+,1      ; Счет количества готовых деталей
  TEST E  X$NDet,Det,Ter1  ; Если готово Det деталей, зафиксировать один прогон
    TEST E  TG1,1,Met4 ; Если в счетчике завершений 1, то расчет результатов моделирования
  SAVEVALUE  Brak,(N$EndOper/X$Prog) ; Количество забракованных деталей, шт.
  SAVEVALUE  DoljaBrak,(X$Brak/(X$Brak+Det); Общая доля брака
  SAVEVALUE  DoljaDet,(Det/(X$Brak+Det))  ; Доля готовых деталей
  SAVEVALUE  Brak,(INT(X$Brak)) ; Количество забракованных деталей (целое), шт.
  SAVEVALUE  TDet,(((AC1-X$AC2)/X$Prog)/60); Среднее время изготовления Det деталей, час
  SAVEVALUE SDet,((X$TDet/Det)#60); Среднее время изготовления одной детали, мин
  SAVEVALUE  AC2,AC1  ; Время предварительных прогонов
  SAVEVALUE  X$Prog,0  ; Обнуление ячейки X$Prog
Met4  SAVEVALUE  NDet,0    ; Обнуление X$NDet
  TERMINATE  1    ; Из счётчика завершений минус 1
Ter1  TERMINATE      ; Вывод вспомогательных транзактов
  START  1000,NP  ; Число предварительных прогонов модели
  RESET        ; Сброс статистики
  START  16641  ; Число основных прогонов модели

В приведенной программе модели для решения обратной задачи в целях сокращения исключён текст до части, имитирующей выполнение 3-й операции, так как он такой же, как и в программе модели для решения прямой задачи. Единственное отличие состоит в том, что в исходные данные следует добавить команду для задания количества деталей, которые нужно изготовить:

Det EQU 9 ; Количество деталей, которые нужно изготовить

Округление до целого количества забракованных деталей производится после расчёта доли готовых и забракованных деталей. Если иначе, то расчёт долей будет некорректным.

В программе модели прямой задачи годные детали после выполнения 3-й операции подсчитывались. Имитирующие их транзакты уничтожались:

EndOper1 TERMINATE ; Счёт готовых деталей

В программе модели обратной задачи годные детали нужно отправить в сегмент организации завершения моделирования. Для этого приведенный только что блок счёта готовых деталей заменён следующим (в тексте программы выше он выделен жирным):

TRANSFER ,Met2 ; Готовые детали

Сегмент имитации работы пункта контроля остаётся неизменным. Остановимся на сегменте завершения моделирования и расчета результатов.

Сохраняемая ячейка NDet служит для счёта текущего количества изготовленных деталей. Как только выполняется условие X$NDet = Det, фиксируется один прогон модели. Det - переменная пользователя, которой задаётся количество деталей, время подготовки которых нужно определить.

Вам уже известно, что модельное время предварительных прогонов не должно учитываться при расчёте среднего времени изготовления 9 деталей. Поэтому оно запоминается в сохраняемой ячейке X$AC2, а при расчёте вычитается из AC1:

SAVEVALUE TDet,(((AC1-X$AC2)/X$Prog)/60) ; Среднее время изготовления Det деталей, час

Проведение исследований

Фрагмент отчёта приведен ниже:

SAVEVALUE     RETRY        VALUE
 PROG           0      16641.000
 BRAK           0          3.000
 DOLJABRAK      0          0.279
 DOLJADET       0          0.721
 TDET           0          7.266
 SDET           0         48.443

В результате решения обратной задачи получим, что Det = 9 деталей будут изготовлены цехом за TDet = 7,266 часа, относительная доля которых составит DoljaDet = 0,721, а среднее время изготовления одной детали SDet = 48,443 мин. При этом будет забраковано Brak = 3 детали, относительная доля которых составит DoljaBrak = 0,279.

SAVEVALUE       RETRY        VALUE
 PROG             0      16641.000
 BRAK             0          3.000
 DOLJABRAK        0          0.278
 DOLJADET         0          0.722
 TDET             0          7.256
 SDET             0         48.374

Видно, что результаты моделирования изменились незначительно. Но если эти изменения для вас несущественны, можно оставить указанное число предварительных прогонов модели в дальнейших исследованиях.

Проведение экспериментов

В "Модель обработки запросов сервером" был проведен дисперсионный анализ с имитационной моделью, предназначенной для решения прямой задачи. Здесь же мы проведём дисперсионный анализ с моделью, решающей обратную задачу.

Исследовать влияние качества 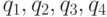выполнения операций на время изготовления D деталей. Значения уровней факторов приведены в табл. 2.2.

Таблица 2.2.

Уровни факторов	Факторы
Нижний	0,1	0,15	0,1	0,2
Верхний	0,25	0,35	0,2	0,9

Результаты моделирования необходимо получить с точностью 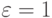мин и доверительной вероятностью 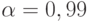. Но поскольку остаётся условие определения относительного числа подготовленных деталей, то количество прогонов остаётся равным 16641, что и в модели для решения прямой задачи.

Некоторые особенности построения для такого случая модели были изложены в п. 2.1.2.1. Однако показатели, которые там определялись в дисперсионном анализе, не были временными. А это является существенным в построении сегмента организации завершения моделирования.

Поскольку результатом моделирования является оценка математического ожидания времени TDet изготовления Det деталей, то в ее вычислении используется абсолютное модельное время АС1 (системный числовой атрибут). При проведении дисперсионного анализа встроенный генератор эксперимента имеет две команды START, а между ними - команда RESET. Команда RESET не влияет на абсолютное модельное время. Поэтому АС1 будет суммой абсолютного модельного времени предварительных прогонов до установившегося режима, обозначим его АС2, и абсолютного модельного времени, пусть АС3, основных прогонов, в ходе которых собирается интересующая нас статистика. Нам для расчетов нужно АС3. Для его получения в программу введены строки:

SAVEVALUE    AC3,(AC1-X$AC2)
SAVEVALUE    AC2,AC1

После предварительных прогонов в ячейке X$Prog сохранится указанное в первой команде START количество прогонов. Эта ячейка используется в первой строке рассматриваемого сегмента и её содержимое должно быть равным нулю. В противном случае модель будет работать неверно. Для предотвращения ошибки введена строка:

SAVEVALUE    X$Prog,0

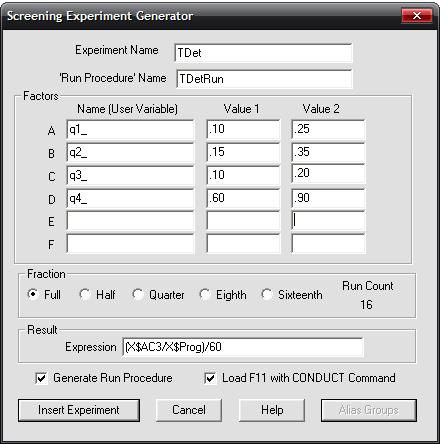
Проведите эксперимент. Как проводится дисперсионный анализ, вы уже знаете. Теме не менее, установите необходимые данные эксперимента согласно рис. 2.2. Укажите число предварительных прогонов 1000 вместо 100, установленных по умолчанию.

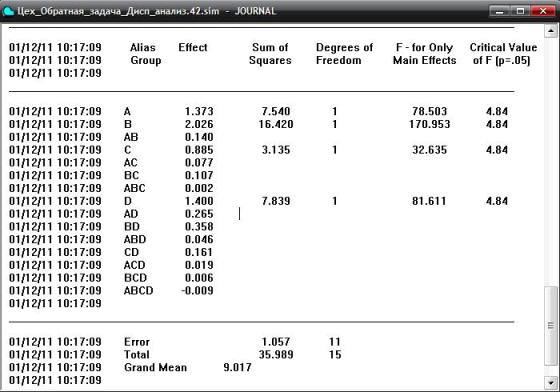
Результаты эксперимента показаны на рис. 2.3. Видно, что все четыре фактора существенные. Наибольшее влияние на функцию отклика оказывает фактор В, что вполне логично, так как из первых трёх он имеет наибольший верхний уровень, т. е. наибольшую долю брака. Наименьшую значимость имеет фактор С, что также объясняется более низким значением доли брака.

Измените непосредственно в процедуре запуска сгенерированного Plus-эксперимента количество предварительных прогонов с 1000 на 100 и запустите модель. Вы получите практически те же самые результаты, например, Grand Mean = 9,006 вместо 9,017.

Рис. 2.2. Диалоговое окно (заполненное) Screening Experiment Generator (Генератор отсеивающего эксперимента)

увеличить изображение
Рис. 2.3. Результаты отсеивающего эксперимента