Семантика баз данных
12.1.2 Атрибуты и шкалы измерения
Элементы данных, хранящиеся в базе, получаются в двух родственных процессах измерения и распознавания. Будем рассматривать процесс измерения как определение термина из словаря результатов измерений, который описывает результат измерения наилучшим, в некотором смысле, способом. Инвариантность результатов измерений определяют шкалы измерений. Формально шкала это отображение 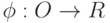 действующее из множества
действующее из множества  измеряемых объектов в множество результатов измерений
измеряемых объектов в множество результатов измерений  . Определяющим компонентом шкалы является либо множество допустимых преобразований результатов измерений, либо обязательный набор отношений.
. Определяющим компонентом шкалы является либо множество допустимых преобразований результатов измерений, либо обязательный набор отношений.
Шкала определяет допустимые способы обработки данных — адекватные статистики, а для некоторых областей, например, социологии может задавать более тонкие свойства, например, существенность, значимость результата измерений.
А нам зачем шкалы? За тем, что они дают еще один смысл, ограничивающий допустимую обработку данных хранящихся в базе.
Существует пять основных шкал — наименований, порядка, интервалов, отношений (подобий) и абсолютная шкала.
Шкала наименований
Допустимые преобразования — любые взаимно однозначные отображения.
Шкала порядка (она же ранговая)
Допустимые преобразования — любые монотонные отображения. Характеризующее множество отношений состоит из двух отношений — эквивалентности и порядка. Пример такой шкалы: бальные оценки успеваемости (например, неудовлетворительно, удовлетворительно, хорошо, отлично), шкала твердости минералов Мооса, в которой выбраны эталоны минералов, а принадлежность к классу определяется по царапанию поверхности.
Заметим, что для данных в шкале порядка среднее значение — неадекватная статистика. В теории функциональных уравнений показано, что, например, уравнение  выполняется только для линейной функции
выполняется только для линейной функции  , а в шкале порядка допустим более широкий класс монотонных преобразований.
, а в шкале порядка допустим более широкий класс монотонных преобразований.
Интервальная шкала (она же шкала разностей)
Часто употребляется для работы с субъективными оценками. Начало отсчета выбирается произвольно, единица измерения задана. Допустимое преобразование — линейное  . В характеризующее множество отношений входят кроме отношения эквивалентности и порядка, еще отношение пропорциональности или суммирования интервалов (разностей). Типичный пример — темпоральные шкалы. В них интервалы времени можно суммировать или вычитать, но складывать даты бессмысленно. Другие примеры: шкалы температур по Цельсию и Фаренгейту. В интервальных шкалах для описания зависимостей можно использовать только отношения интервалов.
. В характеризующее множество отношений входят кроме отношения эквивалентности и порядка, еще отношение пропорциональности или суммирования интервалов (разностей). Типичный пример — темпоральные шкалы. В них интервалы времени можно суммировать или вычитать, но складывать даты бессмысленно. Другие примеры: шкалы температур по Цельсию и Фаренгейту. В интервальных шкалах для описания зависимостей можно использовать только отношения интервалов.
Шкала подобия
Допустимо преобразование подобия (умножение на положительную константу) 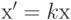 , где
, где  . В характеризующее множество отношений кроме эквивалентности, порядка, пропорциональности входит еще суммирование. Поэтому результаты таких измерений можно обрабатывать в рамках поля вещественных чисел, то есть, используя сложение, вычитание, умножение и деление. Нуль абсолютен и имеет определенный в предметной области смысл. Примеры измеряемых величин: масса, длина, сила, стоимость (цена), температура в абсолютной шкале (Кельвина).
. В характеризующее множество отношений кроме эквивалентности, порядка, пропорциональности входит еще суммирование. Поэтому результаты таких измерений можно обрабатывать в рамках поля вещественных чисел, то есть, используя сложение, вычитание, умножение и деление. Нуль абсолютен и имеет определенный в предметной области смысл. Примеры измеряемых величин: масса, длина, сила, стоимость (цена), температура в абсолютной шкале (Кельвина).
Поскольку в классической физике и инженерном деле предполагается, что все измерения выполняются в шкале подобия, то иногда проявляется странная склонность рассматривать любые измерения как выполненные в этой шкале. Вот тогда школы начинают бороться за неадекватную статистику "средний балл", а недостаточно подготовленные аналитики удивляются тому, что в социологии измеримая величина в некоторых обстоятельствах оказывается незначимой.
Абсолютная шкала
Имеет единственную нулевую точку, характеризующую отсутствие чего-либо. Результат измерения однозначен, не подлежит изменению. Единственное допустимое преобразование тождественное. К множеству отношений шкалы подобия добавляется однозначность определения единицы измерений. Типичный пример — подсчет количества людей в группе.
Уже упоминалось, что шкала полностью определяет осмысленность методов обработки результатов измерения. Для классических шкал адекватны те статистики, которые инвариантны относительно допустимых преобразований используемой шкалы.
Понятие "измеряемая величина" можно обобщить на признаки сложных открытых объектов, используемых в общественных и компьютерных науках, в частности в администрировании программных продуктов и в адаптивных программах. Особенности рассматриваемого класса измеряемых величин связаны с невозможностью адекватного моделирования описываемого объекта вне контекста или вмещающей среды.
Зависимость результата измерения от времени, состояния объекта и системы в целом, от ресурсов имеющихся в распоряжении измеряемого объекта и, наконец, ограниченность размеров ресурсов совместно используемых объектом измерения, другими объектами и измерителем приводят к существенному усложнению модели измеряемой величины.
Возможны интерпретации результата измерения в моделях отличных от модели измерения и распадение измеряемой величины в семейство измеряемых величин.
Пример разделения измеряемой величины "размер таблицы" для системы управления базами данных Oracle. Для размещения таблицы выделяется структура данных называемая сегментом. Сегмент состоит из экстентов, которые представляют набор непрерывно размещенных блоков базы имеющих фиксированный размер. В этом вмещающем пространстве величина "размер таблицы" распадается в следующее семейство измеряемых величин:
- "Размер таблицы" как место, которое не могут занять другие таблицы. Он равен размеру сегмента.
- "Размер таблицы" как количество экстентов занятых данными таблицы.
- "Размер таблицы" как количество блоков занятых данными таблицы.
- "Размер таблицы" как количество байтов занятых данными таблицы.
- "Размер таблицы" как количество символов, выданных при распечатке таблицы. Из-за возможности кодирования, сжатия числовых данных и возможности шифрования "на лету" не совпадает со значением предыдущего параметра.
- "Размер таблицы" определенный как значение параметра High Water Mark, указывающего на последний блок, когда-либо занятый данными таблицы.
Выпишем обычно неявно предполагаемые постулаты классической теории измерений, сделав упор на нюансы важные для рассматриваемого класса измеряемых величин:
- Измеряемый объект есть замкнутая система. Он не взаимодействует с другими объектами и, в частности, с измерителем. Отсюда следует, что его можно без ущерба извлечь из контекста (системы) или вмещающего пространства, и что влиянием измерителя можно пренебречь.
- Измеряемый объект не меняется вообще и тем более во время измерения. Это означает, что результаты измерений выполненных в разное время и с разной длительностью совпадают с точностью до погрешности измерений, и что интерпретация измерения не зависит от времени начала измерения и его длительности.
- Измеряемая величина не имеет ограничений на применимость.
- Результат измерения интерпретируется непосредственно в рамках модели измерения.
- Измеритель и алгоритм измерения не рассматриваются в рамках теории, то есть считаются всегда существующими или, по крайней мере, не заслуживающими внимания.
Заметим, что, по крайней мере, в социологических измерениях невыполнение последних трех пунктов учитывается давно. В общем случае возможны нарушения всех перечисленных постулатов.
Система измеряемых величин может иметь сложную структуру, возможно зависящую от особенностей решаемой задачи и использованного инструментария. Например, план счетов управленческого бухгалтерского учета можно рассматривать как вмещающее пространство, определяющее каждый счет или субсчет как измеряемую величину. Этот план счетов может изменяться в зависимости от целей учета и/или особенностей бизнес-процессов.
Классическая измеряемая величина представляет концепт с двумя обязательными атрибутами:
имя_измеряемой_величины(модель_измерения, результат_измерения)
В общем случае измеряемая величина может иметь более сложную спецификацию:
имя_измеряемой_величины( область_применения, модель_измерения, модель_интерпретации, результат_измерения, параметры_измерения)
В ней атрибут "область_применения" характеризует ограничения на применимость величины, указание моделей измерения и интерпретации отражает различия между измерением и интерпретацией, атрибут "парамет-ры_измерения" характеризует условия, при которых выполнялось измерение.
Ограничения областей существования измеряемых величин одна из основных причин локальности используемых моделей. В отличие от известной практики, когда кусочные описания вызываются техническими причинами, в основном желанием упрощения используемых моделей, в общем случае причины явления лежат глубже, в свойствах самой изучаемой системы. Существенные ограничения на применение моделей делают получаемые знания менее универсальными и выдвигают на первый план аспекты, связанные с классификациями и идентификацией системы и ее признаков.
Очевидно, что сведения о шкалах и особенностях измерений данных, содержащихся в базе, во многих случаях желательно хранить в базе и сделать их доступными информационной системе, основой которой эта база является. В последующих разделах станет понятно, что дополнительная информация об измерениях может храниться как один из элементов семантики данных в виде смыслов.
