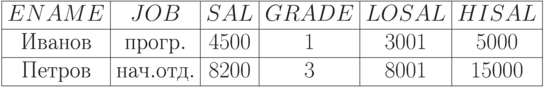НОУ ИНТУИТ | Модели и смыслы данных в Cache и Oracle. Лекция 4: Реляционная модель данных

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Кубанский государственный университет

Опубликован: 24.12.2013 | Доступ: свободный | Студентов: 682 / 9 | Длительность: 24:28:00

Тема: Базы данных

Специальности: Администратор баз данных

|

Вам нравится? Нравится 15 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

4.4 Теорема Хиса

Докажем теорему Хиса (Heath), устанавливающую связь между функциональными зависимостями в схеме отношения и способом его полной декомпозиции. Она определяет условия при которых декомпозиция будет полной.

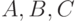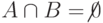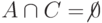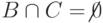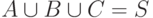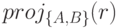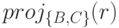Теорема Хиса. Пусть в отношении со схемой R(S) , где — полный набор атрибутов отношения, выделены три набора атрибутов A,B,C таких что $A \cap B=\not 0$ , $A \cap C=\not 0$ , $B \cap C=\not 0$ , $A \cup B \cup C=S$ . Тогда, если набор функционально зависит от , то проекции $proj_{\{A,B\}}(r)$ , $proj_{\{B,C\}}(r)$ образуют полную декомпозицию отношения .

Доказательство. Введем вспомогательное отношение

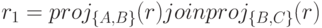$r_1=proj_{\{A,B\}}(r) {join} {proj_{\{B,C\}}(r)}$

( 4.1)

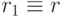как соединение двух проекций отношения . Покажем, что $r_1\equiv r$ .

Выберем произвольную запись (кортеж) 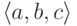$\langle{a,b,c}\rangle$ из . Так как

$\langle{a,b}\rangle \in proj_{\{A,B\}}(r)$ , a

$\langle{b,c}\rangle \in proj_{\{B,C\}}(r)$

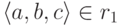то по свойству операции соединения $\langle{a,b,c}\rangle \in r_1$ .

Следовательно,
$r\subseteq r_1$ ( 4.2)
Выберем произвольный кортеж 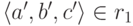$\langle {a',b',c'}\rangle \in r_1$ . Из (4.1) следует, что

$\langle {a',b'}\rangle \in proj_{\{A,B\}}(r)$ ( 4.3)

$\langle {b',c'}\rangle \in proj_{\{B,C\}}(r)$ ( 4.4)

Значит в существуют записи

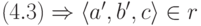
$(4.3)\Rightarrow \langle {a',b',c}\rangle \in r$ ( 4.5)

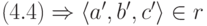
$(4.4)\Rightarrow \langle {a',b',c'}\rangle \in r$ ( 4.6)

Но функционально зависит от . Поэтому в кортежах (4.5) и (4.6) 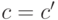, а значит запись 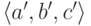$\langle {a',b',c'}\rangle$ входит в отношение , иначе говоря

$r_1\subseteq r$ ( 4.7)
Сопоставляя (4.2) и (4.7), получаем 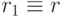$r_1\equiv r$ . Иначе говоря, декомпозиция (4.1) полная.

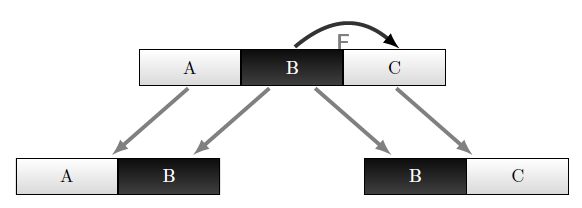
Мнемоническое изображение декомпозиции по теореме Хиса даёт рисунок 4.6

Рис. 4.6. Мнемоника для теоремы Хиса

4.5 Структура и особенности реляционной алгебры

Отношение определяется своей схемой . Набор записей в отношении определяет его состояние. При этом повторяющиеся кортежи в отношении отсутствуют.

Как вы помните, операция в любой алгебре над некоторым множеством даёт результат, принадлежащий этому же множеству Реляционная алгебра строится над множеством отношений. Поэтому в реляционной модели при выполнении операций создаются новые, может быть временные, отношения на основе набора уже имеющихся отношений. Средств для создания отношений, не выводимых из имеющихся нет. Изменять состояния отношений, то есть заполнять их кортежами, в реляционной модели невозможно. Иначе говоря, реляционная алгебра —это модель запросов к базе.

Реляционная алгебра определяется на конечном множестве отношений с фиксированной сигнатурой и конечным числом кортежей. Поскольку сигнатуры отношений могут не совпадать, реляционная алгебра многосортна. Сами отношения и кортежи разных отношений могут быть не сравнимы.

Ещё раз обращаем внимание на то, что набор схем отношений предполагается заданным заранее. Реляционная алгебра не изменяет его и не может изменять состояние отношений, то есть вводить, удалять и изменять записи. Манипуляции данными создают врeменные, не сохраняемые отношения.

Обратите внимание на то, что в реляционной модели кроме алгебры могут использоваться исчисления, которыми мы займёмся в "Языки реляционных баз данных" .

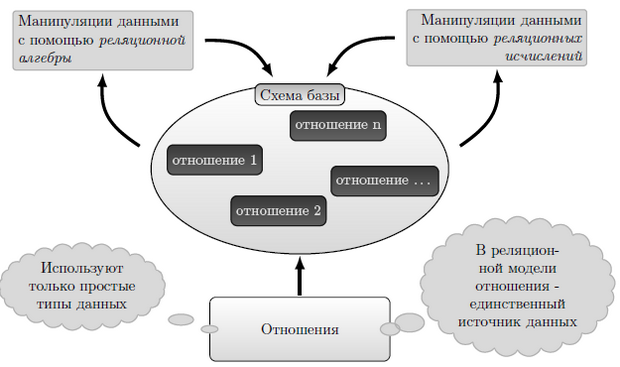
Сводка некоторых особенностей реляционной модели приведена на рисунке 4.7.

Рис. 4.7. Некоторые особенности реляционной модели

4.6 Операции реляционной алгебры

Полный перечень операций реляционной алгебры:

Проекция.
Естественное соединение.
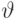$\vartheta$ — соединение.
Декартово произведение.
Селекция.
Булевы операции.
Частное.
Переименование атрибутов.

Все операции за исключением переименования работают с содержимым отношений. Результат операции есть новое отношение. Над ним так же можно выполнять операции.

Первые две операции, проекция и естественное соединение, позволили нам разобраться с декомпозицией отношений, сформулировать и доказать теорему Хиса. Изучим все остальные операции, не затрагивая пока переименования атрибутов.

4.6.1 υ-соединение

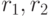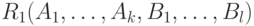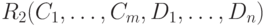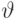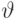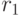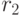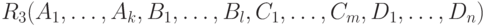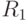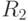Определение. Пусть даны отношения r_1,r_2 со схемами $R_1(A_1,\dots,A_k,B_1,\dots,B_l)$ и $R_2(C_1,\dots,C_m,D_1,\dots,D_n)$ соответственно; $\vartheta$ —оператор сравнения на группах атрибутов и . Тогда $\vartheta$ -соединение отношений r_1 и r_2 есть отношение со схемой $R_3(A_1,\dots,A_k,B_1,\dots,B_l,C_1,\dots,C_m,D_1,\dots,D_n)$ , полученной объединением атрибутов схем R_1 и R_2 без повторения. 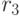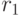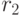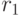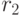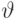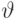Записи r_3 получаются конкатенацией тех записей из r_1 и r_2 , у которых значения группы столбцов в r_1 и группы столбцов в r_2 находятся в отношении $\vartheta$ (удовлетворяют $\vartheta$ ).

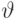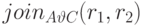Обозначение $\vartheta$ -соединения: $join_{A\vartheta C}(r_1,r_2)$ .

Замечание. Очевидно, если в качестве 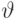$\vartheta$ взять равенство "=" и 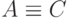$A\equiv C$ , получим естественное соединение со схемой

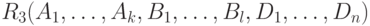$R_3(A_1,\dots,A_k,B_1,\dots,B_l,D_1,\dots,D_n)$ .

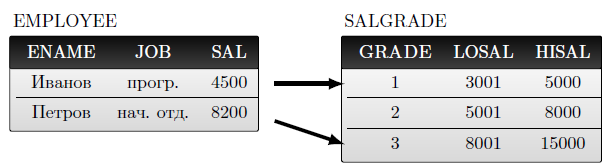
Рассмотрим пример 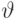$\vartheta$ -соединения для отношений employee и salgrade, то есть "работник" и "категория оплаты":

Отношение employee:

$EMPLOYEE: \begin{array}{|c|c|c|} \hline ENAME & JOB & SAL \\ \hline \end{array}$

Отношение salgrade:

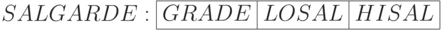
$SALGARDE: \begin{array}{|c|c|c|} \hline GRADE & LOSAL & HISAL \\ \hline \end{array}$

По условию 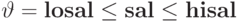$\vartheta=\mathbf{losal} \le \mathbf{sal} \le \mathbf{hisal}$ с вариантом заполнения (т.е. состоянием), изображённым на рисунке 4.8, даст отношение, приведенное ниже. Здесь grade — категория оплаты, losal и hisal, соответственно, минимальная и максимальная зарплаты данной категории.

Рис. 4.8. Прим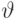ер заполнения исходных отношений

Результат $\vartheta$ -соединения:

$\begin{array}{|c|c|c|c|c|c|} \hline ENAME & JOB & SAL & GRADE & LOSAL & HISAL\\ \hline Иванов & прогр. & 4500 & 1 & 3001 & 5000 \\ \hline Петров & нач. отд. & 8200 & 3 & 8001 & 15000\\ \hline \end{array}$

Дальше >>

Авторизоваться

Модели и смыслы данных в Cache и Oracle

Реляционная модель данных

4.4 Теорема Хиса

4.5 Структура и особенности реляционной алгебры

4.6 Операции реляционной алгебры

4.6.1 υ-соединение

Вопросы и ответы