Реляционная модель данных
4.13 Об алгебре Дейта и Дарвена и перспективах развития реляционной модели
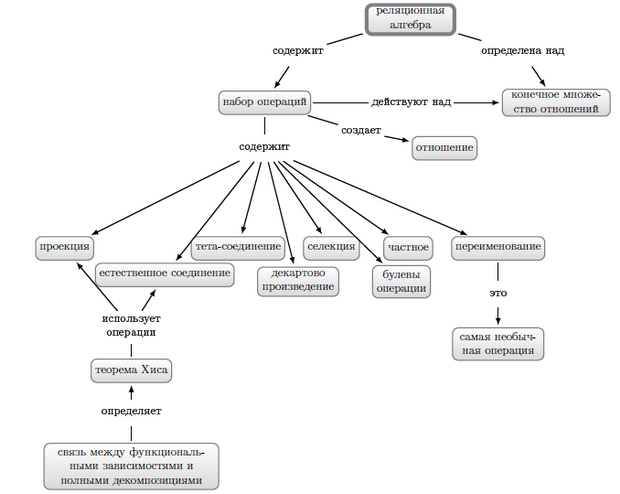
Реляционная алгебра Кодда, один из вариантов которой мы изучили, удобна тем, что семантика языка SQL, который мы рассмотрим в "Язык SQL" основывается именно на этой алгебре. Существует ряд расширений алгебры Кодда.
Дейтом и Дарвеном был предложен новый вариант реляционной алгебры, с минимальным набором базисных операций. В него входят реляционное дополнение, реляционная конъюнкция (или дизъюнкция) и проекция (удаление атрибута). Использование реляционного дополнения возможно, поскольку предполагается, что домен имеет конечную мощность. Реляционная конъюнкция понимается как некоторое обобщение естественного соединения определённого в алгебре Кодда. Операция переименования, понимаемая как замена имени ровно одного из атрибутов отношения, оказывается зависимой. С помощью константного отношения, представляющего таблицу перехода значений при замене имён атрибута, переименование представляется через операции реляционной конъюнкции и удаления атрибута.
Можно показать, что новая алгебра полна, то есть все операции алгебры Кодда выражаются через операции алгебры Дейта и Дарвена.
Важным преимуществом нового варианта реляционной алгебры является более точная связь с логикой. Однако, для наших целей достаточно результата Джекобса, показавшего, что и иерархическая, и сетевая, и реляционная модели основываются на многосортной логике. Изучить основы алгебры Дейта и Дарвена лучше всего по книгам Кузнецова С.Д., например, [Кузнецов С.Д. Основы баз данных: курс лекций: учебное пособие. - М.: Интернет-Ун-т Информ. Технологий, 2005. - 488 с.].
Исходя из множественности математических моделей понятия "реляционная модель данных" можно предположить, что и другие понятия в базах данных и вообще в информатике могут иметь несколько экспликаций (так называется методологический прием замещения неточного понятия или представления точным понятием). Важно выбрать в некотором смысле "минимальный", либо наиболее удобный, как-то "согласованный" вариант. Это обстоятельство следует иметь в виду, рассматривая в дальнейшем отображения моделей данных.
Как известно, в последние двадцать лет в компьютерных науках наметился разрыв между работой теоретиков и практическими реализациями [Парнас Д.Л. Реальное переосмысление "формальных методов". Оригинал: David Lorge Parnas. Really Rethinking "Formal Methods". Computer (IEEE Computer Society), V. 43, No 1, January 2010]. Есть основания полагать, что главная причина такого положения дел в том, что для правильного понимания перспектив использования теоретических построений в практике, следует учитывать следующие пять аспектов:
- свойства (вид, тип) моделей, возможность их представления математическими структурами;
- лингвистическая компонента, в частности, учёт того, что языки моделей, языки программирования — это ещё и искусственные языки, распространённые в определённых группах людей;
- особенности аппаратных реализаций моделей;
- стоимость работ, связанных с переходом на новые модели;
- влияние маркетинговых соображений.
Как отмечено Парнасом, ". . . многие исследовательские работы пишутся так, будто только математика и имеет значение". Многие практически важные модели слишком сложны и, главное, не позволяют эффективно обрабатывать информацию. Это ограничивает их возможности. Как это ни тривиально, но модель должна быть адекватной с учётом более одного из упомянутых пяти аспектов.
Учёт лингвистической компоненты, точнее когнитивных аспектов, связанных с особенностями восприятия искусственного языка человеком, позволяет оптимизировать деятельность самого слабого звена в системах разработки программного обеспечения, то есть человека.
Особенности реализации, в том числе аппаратные, могут быть критическими. Так, в реализации алгебры Кодда широкое использование декартова произведения приводило к созданию промежуточных таблиц таких размеров, что от этого подхода давно отказались.
И, наконец, если мы говорим о реализациях, то необходимо понимать, что они выполняются конкретными организациями, работающими в конкурентной среде и требуют вполне определённых материальных затрат. Трудно представить вендора, который заменяет старую отлаженную СУБД на принципиально новую и тем самым обрекает себя на повторение пути, который уже был пройден и позволил решить массу частных проблем.
Так что шансы модели Дейта-Дарвена на реализацию следует оценить как незначительные. Что касается методов выработанных в маркетинге, то видимо подход, основанный на выделении сегментов рынка и установлении соответствия продукта некоторым сегментам, по-видимому, можно перенести на разработки моделей. Конечно, в этой ситуации следует рассматривать не рынок в собственном смысле слова, а предметную область, а сегменты рынка заменить набором парадигм, действующих и возможных, задав их определяющие свойства.
4.14 Основные понятия главы
К определению реляционной алгебры:
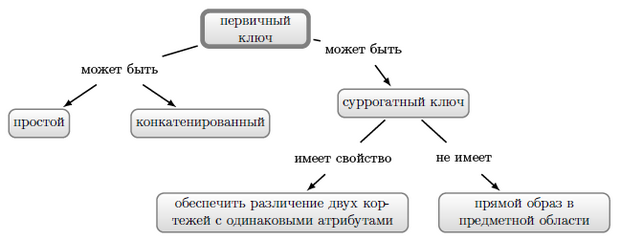
Понятие ключа было достаточно подробно исследован в "Модель сущность-связь" . Семантическая сеть для этого понятия приведена в разделе 2.3. Напомним, что, говоря "первичный ключ", мы на самом деле имеем в виду "минимальный первичный ключ".
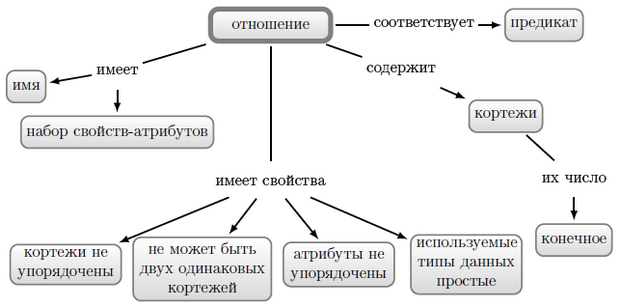
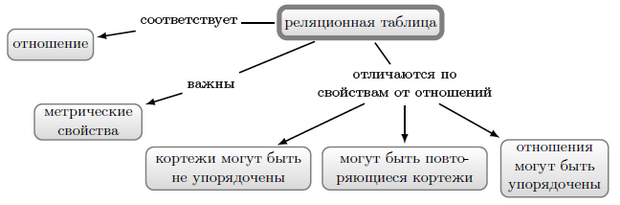
Отношения и их связи с таблицами, которые представляют отношения в реализации баз данных.
Число кортежей и атрибутов предполагается конечным. Важно помнить, что отношение не обладает метрическими свойствами, такими как число кортежей и размер значения атрибутов. Для таблиц, представляющих отношения, возможны упорядочения, а метрические свойства исключительно важны. Они определяют объём памяти, время выполнения команд.
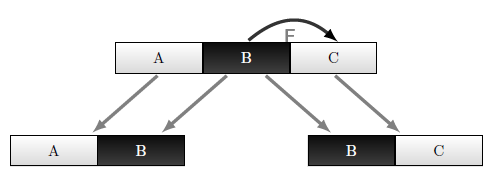
Мнемоника для теоремы Хиса в виде таких "шортиков":