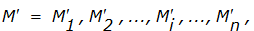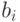Методы защиты информации в компьютерных системах и сетях
3.7. Криптографические протоколы
Успешное решение задачи открытого распределения ключей, создание практических схем электронной подписи способствовало возникновению нового направления криптографии - теории криптографических протоколов. Для современных информационных систем характерен перевод всего документооборота в электронную форму. Возникающие при этом проблемы чаще всего могут быть решены только с использованием возможностей криптографии.
Типичный пример: взаимодействуют два удаленных абонента А (клиент банка) и В (банк). Абонент А хочет доказать абоненту В, что он тот, за кого себя выдает, а не злоумышленник. Для решения этой задачи требуется протокол аутентификации абонента. В каждом конкретном случае для обеспечения юридической значимости пересылаемых электронных документов требуется использование соответствующих криптографических протоколов, которые за последние годы превратились в основной объект исследований криптографии.
3.7.1. Основные понятия
Объектом изучения теории криптографических протоколов являются удаленные абоненты, взаимодействующие по открытым каналам связи. Целью взаимодействия является решение какой-либо практической задачи. Модель предусматривает наличие противника, преследующего собственные цели. Противник может выдавать себя за законного субъекта взаимодействия, вмешиваться в информационный обмен между абонентами и т.п. Участники протокола в общем случае не доверяют друг другу, другими словами, некоторые протоколы должны быть рассчитаны на ситуацию, когда противником может оказаться даже один из абонентов или несколько абонентов, вступивших в сговор. В настоящее время известно около трех десятков различных типов протоколов. Все эти типы можно разделить на две группы:
- прикладные протоколы, решающие конкретную задачу, которая может возникнуть на практике;
- примитивные протоколы, которые используются в качестве своеобразных строительных блоков при создании прикладных протоколов.
Типы протоколов приведены на рис. 3.25.
Протокол чаще всего является интерактивным, т.е. предусматривает многораундовый обмен сообщениями между участниками и включает в себя:
- распределенный алгоритм, т.е. характер и последовательность действий каждого из участников;
- спецификацию форматов пересылаемых сообщений;
- спецификацию синхронизации действий участников;
- описание действий при возникновении сбоев.
3.7.2. Доказательства с нулевым разглашением
Существенное влияние на разработку многих криптографических протоколов оказали исследования двух математических моделей - интерактивной системы доказательств (Interactive Proof System) и доказательств с нулевым разглашением знаний (Zero-Knowledge Proofs).
Интерактивная система доказательств суть протокол (P, V, S) взаимодействия двух субъектов: доказывающего (претендента) P и проверяющего (верификатора) V. Абонент P хочет доказать V, что утверждение S истинно. При этом считается, что абонент V самостоятельно проверить утверждение S не в состоянии, что абонент V не может быть противником, а абонент P может быть противником, пытающимся доказать истинность ложного утверждения S. Протокол, состоящий из некоторого числа раундов обмена сообщениями между P и V, должен удовлетворять двум условиям:
- полнота - если S действительно истинно, то доказывающий убедит проверяющего признать это;
-
корректность - если S ложно, то доказывающий не сможет убедить проверяющего в обратном.
Если предположить, что V может быть противником, который хочет получить информацию об утверждении S, необходим протокол (P, V, S), называемый доказательством с нулевым разглашением, удовлетворяющий помимо перечисленных еще и следующему условию:
- нулевое разглашение - в результате работы протокола абонент V не увеличит своих знаний об утверждении S.
Иными словами, в результате реализации протокола абонент P сможет доказать абоненту V, что он владеет некоторой секретной информацией, не разглашая ее сути.
Упрощенно процедуру доказательства с нулевым разглашением можно представить следующим образом. Проверяющий задает серию случайных вопросов, каждый из которых допускает ответ "да" или "нет". После первого вопроса проверяющий убеждается в том, что доказывающий заблуждается с вероятностью 1/2. После второго вопроса проверяющий убеждается в том, что доказывающий заблуждается с вероятностью 1/4, и т.д. (после каждого вопроса знаменатель удваивается). После 100 вопросов вероятность того, что доказывающий заблуждается или не располагает доказательством (не владеет секретной информацией), становится настолько близкой к нулю, что даже у самого "недоверчивого" проверяющего не должно остаться сомнений в справедливости доказываемого утверждения. После 300 вопросов знаменатель достигает величины, которая превосходит число атомов во Вселенной.
Роль доказательств с нулевым разглашением особенно велика при реализации протоколов аутентификации. Допустим, например, Р - алгоритм, реализованный в интеллектуальной карточке клиента (абонент А) банка, V - программа, выполняемая компьютером банка (абонент В). Перед выполнением любой операции банк должен убедиться в подлинности карточки и идентифицировать ее владельца. Если для этой цели использовать протокол (P, V, S), свойство полноты позволит карточке доказать свою аутентичность; свойство корректности защитит интересы банка от злоумышленника, который попытается воспользоваться фальшивой карточкой; свойство нулевого разглашения защитит клиента от злоумышленника, который попытается пройти аутентификацию под именем абонента А, воспользовавшись информацией, перехваченной во время предыдущих раундов аутентификационного обмена. Аналогичных результатов можно добиться, используя методы доказательств с нулевым разглашением для создания не поддающихся подделке удостоверений личности.
3.7.3. Протоколы разделения секрета
Эффективным методом защиты является разделение доступа (не путать с разграничением доступа), разрешающее доступ к секретной информации только при одновременном предъявлении своих полномочий участниками информационного взаимодействия, не доверяющих друг другу. Протоколы или схемы разделения секрета (СРС) (Secret Sharing Scheme) позволяют распределить секрет между n участниками протокола таким образом, чтобы заранее заданные разрешенные множества участников могли однозначно восстановить секрет, а неразрешенные - не получали бы никакой информации о возможном значении секрета. Выделенный участник протокола, распределяющий доли (share) секрета, обычно называется дилером (D).
Пусть M - защищаемая информационная последовательность (битовая строка) длиной m. Простейшая схема разделения секрета между тремя абонентами A, B и C имеет следующий вид.
- Дилер D вырабатывает две случайные битовые строки
 и
и 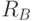 длиной m и вычисляет
длиной m и вычисляет 
- D передает абоненту A информационную последовательность
 , абоненту B - информационную последовательность
, абоненту B - информационную последовательность 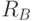 и абоненту C - информационную последовательность
и абоненту C - информационную последовательность 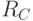 .
. - Чтобы прочитать информацию M абонентам А, В и С необходимо предъявить свои доли секрета
 ,
, 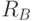 и
и  длиной m и вычислить
длиной m и вычислить  .
.
Шаги 1 и 2 - это стадия распределения долей секрета. Шаг 3 - стадия восстановления секрета. Каждая доля секрета сама по себе не имеет никакого смысла, но если их сложить, смысл исходной информационной последовательности полностью восстанавливается. При правильной реализации приведенный протокол полностью безопасен, так как для закрытия информации применяется абсолютно стойкий шифр, описанный ранее, и поэтому никакие вычисления не смогут помочь при попытке определить секрет по одной или двум его частям. Аналогичную схему можно легко реализовать для любого числа участников.
Рассмотрим схему разделения доступа Шамира. Пусть n - число участников протокола, GF (p) - конечное поле из p элементов, p - простое, p > n. Поставим в соответствие каждому i-му участнику ненулевой элемент поля  и, положим,
и, положим, 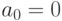 .
.
Схема разделения доступа Шамира.
-
Стадия распределения долей секрета
 . Дилер СРС вырабатывает t – 1 независимых равномерно распределенных на GF (p) случайных чисел
. Дилер СРС вырабатывает t – 1 независимых равномерно распределенных на GF (p) случайных чисел
и посылает каждому i-му участнику соответствующее ему значение
многочлена
 , где
, где 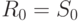 .
. -
Стадия восстановления секрета. Учитывая, что любой многочлен степени t – 1 однозначно восстанавливаются по его значениям в произвольных t точках, то любые t участников могут восстановить многочлен F (X), а значит, найти значение секрета по формуле
 . По этой же причине для любых t – 1 участников, любых значений
. По этой же причине для любых t – 1 участников, любых значений 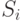 и любого секрета
и любого секрета  существует только один соответствующий им многочлен, для которого справедливо
существует только один соответствующий им многочлен, для которого справедливо
 .
.
Схемы подобного типа находят применение при построении пороговых структур доступа и носят название (n, t)-пороговых СРС. Такие схемы, например, позволяют владельцу некоей секретной информации распределить эту информацию при хранении на n своеобразных ее дубликатов таким образом, что ему для восстановления секрета достаточно получить доступ к любым t из них. При этом никакие t – 1 дубликатов не предоставляют никакой информации об этом секрете.
3.8. Контроль целостности информации
3.8.1. Аутентичность. Задача аутентификации информации
В информационных системах помимо обеспечения секретности информации необходимо также решать не менее важную задачу аутентификации обрабатываемых массивов данных. Информация может считаться аутентичной, когда потребитель имеет гарантии, во-первых, целостности информации, а во-вторых, ее авторства, иначе говоря, подлинности.
Иногда ошибочно считается, что задача защиты целостности решается простым шифрованием. На первый взгляд кажется, что это действительно так. В зашифрованный массив данных трудно внести какие-то осмысленные изменения, потому что с вероятностью, близкой к единице, факты искажения становятся очевидными после расшифрования, например вместо текста на русском языке появляется бессмысленный набор символов. Наконец, для классических криптосистем только пользователи, обладающие секретным ключом, могут зашифровать сообщение, и значит, если получатель принял сообщение, зашифрованное на его секретном ключе, он может быть уверен в его авторстве.
На самом деле приведенные рассуждения ошибочны. Искажения, внесенные в зашифрованные данные, становятся очевидны после расшифрования только в случае большой избыточности исходных данных. Эта избыточность имеет место лишь в некоторых частных случаях, например когда исходная информация является текстом на естественном или искусственном языке. В общем случае требование избыточности данных может не выполняться, а это означает, что после расшифрования модифицированных данных они по-прежнему могут поддаваться интерпретации.
При использовании симметричной криптосистемы факт успешного расшифрования данных, зашифрованных на секретном ключе, может подтвердить их авторство лишь для самого получателя. Третий участник информационного обмена, арбитр, при возникновении споров не сможет сделать однозначного вывода об авторстве информационного массива, так как его автором может быть каждый из обладателей секретного ключа, а их, как минимум, двое.
Таким образом, секретность и аутентичность суть различные свойства информационных систем, поэтому традиционно задачи обеспечения секретности и аутентичности решаются различными средствами.
3.8.2. Имитозащита информации. Контроль целостности потока сообщений
На всех этапах своего жизненного цикла информация может подвергаться случайным и умышленным разрушающим воздействиям. Для обнаружения случайных искажений информации применяются корректирующие коды, которые в некоторых случаях позволяют не только зафиксировать факт наличия искажений информации, но и локализовать и исправить эти искажения. Умышленные деструктивные воздействия чаще всего имеют место при хранении информации в памяти компьютера и при ее передаче по каналам связи. При этом полностью исключить возможность несанкционированных изменений в массивах данных не представляется возможным. Поэтому крайне важно оперативно обнаружить такие изменения, так как в этом случае ущерб, нанесенный законным пользователям, будет минимальным. Целью противника, навязывающего ложную информацию, является выдача ее за подлинную, поэтому своевременная фиксация факта наличия искажений в массиве данных сводит на нет все усилия злоумышленника. Таким образом, под имитозащитой понимают не исключение возможности несанкционированных изменений информации, а совокупность методов, позволяющих достоверно зафиксировать их факты, если они имели место.
Для обнаружения искажений в распоряжении законного пользователя (например, получателя информации при ее передаче) должна быть некая процедура проверки Т (М), дающая на выходе 1 (если в массиве данных М отсутствуют искажения) или 0, если такие искажения имеют место. С целью ограничения возможностей противника по подбору информационной последовательности М` (M`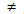 M), где М - правильная последовательность (без искажений), для которой Т (М`) = 1, идеальная процедура такой проверки должна обладать следующими свойствами:
M), где М - правильная последовательность (без искажений), для которой Т (М`) = 1, идеальная процедура такой проверки должна обладать следующими свойствами:
- невозможно найти сообщение М` способом, более эффективным, чем полный перебор по множеству допустимых значений М` (такая возможность в распоряжении противника имеется всегда);
- вероятность успешно пройти проверку у случайно выбранного сообщения М` не должна превышать заранее установленного значения.
Учитывая, что в общем случае все возможные значения М могут являться допустимыми, второе условие требует внесения избыточности в защищаемый массив данных. При этом чем больше разница N между размером преобразованного избыточного М* и размером исходного М-массивов, тем меньше вероятность принять искаженные данные за подлинные - эта вероятность равна  .
.
На рис. 3.26 показаны некоторые возможные варианты внесения такой избыточности. В роли неповторяющегося блока данных nrb могут выступать метка времени, порядковый номер сообщения и т.п. В роли контрольного кода могут выступать имитоприставка (код МАС) или электронная подпись. Имитоприставкой принято называть контрольный код, который формируется и проверяется с помощью одного и того же секретного ключа.
увеличить изображение
Рис. 3.26. Схемы контроля целостности: а - с использованием зашифрования; б - с формированием контрольного кода; в - с формированием контрольного кода и зашифрованием
Использование блока nrb позволяет контролировать целостность потока сообщений, защищая от повтора, задержки, переупорядочения или их утраты. При использовании в качестве nrb порядкового номера получатель, приняв (i + 1)-е сообщение, проверяет равенство  , т.е. его номер на единицу больше номера предыдущего i-го сообщения. При использовании в качестве nrb метки времени получатель контролирует соответствие времени отправки и приема сообщений. Они должны соответствовать друг другу с учетом задержки в канале связи и разности показаний часов отправителя и получателя. Целостность потока сообщений можно также контролировать, используя зашифрование со сцеплением сообщений, схема которого приведена на
рис.
3.27.
, т.е. его номер на единицу больше номера предыдущего i-го сообщения. При использовании в качестве nrb метки времени получатель контролирует соответствие времени отправки и приема сообщений. Они должны соответствовать друг другу с учетом задержки в канале связи и разности показаний часов отправителя и получателя. Целостность потока сообщений можно также контролировать, используя зашифрование со сцеплением сообщений, схема которого приведена на
рис.
3.27.
Самый естественный способ преобразования информации с внесением избыточности - это добавление к исходным данным контрольного кода S фиксированной разрядности N, вычисляемого как некоторая функция от этих данных:

В этой ситуации выделение исходных данных из преобразованного массива М* суть простое отбрасывание контрольного кода S. Проверка же целостности заключается в вычислении для содержательной части М` полученного массива данных контрольного кода  и сравнении его с переданным значением S. Если они совпадают, сообщение считается подлинным, в противном случае - ложным, т.е.
и сравнении его с переданным значением S. Если они совпадают, сообщение считается подлинным, в противном случае - ложным, т.е.
T (M`) = 1, если S = F (M`), и T (M`) = 1, если S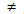 F (M`).
F (M`).
Функция F формирования контрольного кода должна удовлетворять следующим требованиям:
- она должна быть вычислительно необратимой, т.е. подобрать массив данных под заданный контрольный код можно только путем полного перебора по пространству возможных значений М;
- у противника должна отсутствовать возможность сформировать ложный массив данных (или ложное сообщение) М` и снабдить его корректно вычисленным контрольным кодом S = F (M`).
Второе свойство можно обеспечить двумя способами: либо сделать функцию F зависимой от некоторого секретного параметра (ключа), либо пересылать контрольный код отдельно от защищаемых данных.
Простейшим примером кода S является контрольная сумма блоков массива данных. Например, если
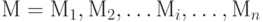 ,
,
то
Однако такое преобразование непригодно для имитозащиты, так как контрольная сумма не зависит от взаимного расположения блоков, а самое главное, соответствующее преобразование не является криптографическим.
Процедура подбора данных под заданную контрольную комбинацию чрезвычайно проста. Допустим, некий массив данных M имеет контрольную сумму S. Тогда для внесения необнаруживаемых искажений противнику достаточно дополнить произвольный ложный массив
еще одним блоком
3.8.3. Криптографические методы контроля целостности
Можно выделить три основных криптографических подхода к решению задачи защиты информации от несанкционированных изменений данных:
- формирование (в режимах CBC или CFB) с помощью функции зашифрования E блочного шифракода аутентификации сообщений MAC (Message Authentication Code);
- формирование с помощью необратимой функции сжатия (хеш-функции) информации кода обнаружения манипуляций с данными MDC (Manipulation Detection Code);
- формирование контрольного кода HMAC (hashed MAC) путем последовательного выполнения операций хеширования и шифрования.
Три основных криптографических подхода в виде схемы приведены на рис. 3.28.

Рис. 3.28. Схемы формирования контрольных кодов целостности: а - МАС, б - MDC (с использованием функции зашифрования блочного шифра), в - НМАС
В таблице 3.1 приведена сравнительная характеристика трех указанных подходов.
| Параметр | MAC | MDC | HMAC |
|---|---|---|---|
| Используемое преобразование | Функция зашифрования Е блочного шифра | Хеш-функция h (x) | Функция зашифрования Е блочного шифра и хеш-функция h (x) |
| Секретная информация | Секретный ключ K | Нет | Секретный ключ K |
| Возможность для противника вычислить контрольный код | Отсутствует | Присутствует | Отсутствует |
| Хранение и передача контрольного кода | Вместе с защищаемыми данными | Отдельно от защищаемых данных | Вместе с защищаемыми данными |
| Дополнительные условия | Требует предварительного распределения ключей | Необходим аутентичный канал для передачи контрольного кода | Требует предварительного распределения ключей |
| Предпочтительная область использования | Защита при передаче данных | Защита при разовой передаче данных, контроль целостности хранимой информации | Защита при передаче данных |
| Относительное быстродействие | Низкое | Высокое (при использовании быстродействующих хеш-функций) | Среднее (при использовании быстродействующих хеш-функций) |
Код аутентификации сообщений. Формирование кода MAC с использованием функции зашифрования блочного шифра официально или полуофициально закреплено во многих государственных стандартах шифрования. Имитоприставка ГОСТ 28147-89 является классическим примером кода MAC. Код аутентификации сообщений может формироваться в режимах CBC или СFB, обеспечивающих зависимость последнего блока шифротекста от всех блоков открытого текста. В случае использования преобразования Е для выработки контрольного кода требования к нему несколько отличаются от требований при его использовании для зашифрования: во-первых, не требуется свойство обратимости, во-вторых, его криптостойкость может быть снижена (например, за счет уменьшения числа раундов шифрования, как в ГОСТ 28147-89). Действительно, в случае выработки кода MAC преобразование всегда выполняется в одну сторону, при этом в распоряжении противника есть только зависящий от всех блоков открытого текста контрольный код, в то время как при зашифровании у него имеется набор блоков шифротекста, полученных с использованием одного секретного ключа.
Код обнаружения манипуляций с данными. MDC есть результат действия хеш-функции. Иначе говоря, MDC - это хеш-образ (дайджест) сообщения М, к которому применили хеш-функцию, т.е. S = h (M). Основное требование к хеш-функции: не должно существовать способа определения массива данных М, имеющего заданное значение хеш-образа h (M), отличного от перебора по всему множеству возможных значений p. Наиболее простой способ построения хеш-функции основан на использовании вычислительной необратимости относительно ключа К функции зашифрования Е любого блочного шифра. Даже при известных блоках открытого М и закрытого С = Е (М) текстов ключ К не может быть определен иначе как перебором по множеству всех возможных значений. Итак, схема формирования хеш-образа сообщения М, обладающая гарантированной стойкостью, равной стойкости используемого шифра, может быть следующей:
- массив данных p разбивается на блоки фиксированного размера, равного размеру ключа К используемого блочного шифра, т.е.:
 ;
; - если последний блок
 неполный, он дополняется каким-либо образом до нужного размера |К|;
неполный, он дополняется каким-либо образом до нужного размера |К|; - хеш-образ сообщения вычисляется следующим образом:
Задача подбора массива данных:
под заданный контрольный код S эквивалентна решению системы уравнений, которую необходимо решить для определения ключа для заданных блоков открытого и закрытого (в режиме простой замены) сообщений. При этом в рассматриваемой ситуации нет необходимости решать всю систему
достаточно решить только одно уравнение S относительно 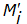 :
:
остальные блоки массива M могут быть произвольными. Но и эта задача в случае использования надежной функции Е вычислительно неразрешима.
К сожалению, приведенная схема формирования MDC не учитывает наличия так называемых побочных ключей шифра. Если для К`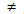 К справедливо
К справедливо
 ,
,
то такой К` и является побочным ключом, т.е. ключом, дающим при зашифровании блока 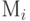 точно такой же результат, что и истинный ключ К. Обнаружение противником побочного ключа при дешифровании сообщения не является особым успехом, так как с вероятностью, близкой к 1, на этом найденном побочном ключе он не сможет правильно расшифровать другие блоки закрытого текста, учитывая, что для различных блоков побочные ключи в общем случае также различны.
точно такой же результат, что и истинный ключ К. Обнаружение противником побочного ключа при дешифровании сообщения не является особым успехом, так как с вероятностью, близкой к 1, на этом найденном побочном ключе он не сможет правильно расшифровать другие блоки закрытого текста, учитывая, что для различных блоков побочные ключи в общем случае также различны.
В случае выработки кода MDC ситуация прямо противоположна: обнаружение побочного ключа означает, что противник нашел такой ложный блок данных, использование которого не изменяет контрольного кода.
Для уменьшения вероятности навязывания ложных данных в результате нахождения побочных ключей при преобразовании применяются не сами блоки исходного сообщения, а результат ихрасширения по некоторому алгоритму. Под расширением понимается процедура получения блока данных большего размера из блока данных меньшего размера. Например, для криптоалгоритма, в котором размер ключа равен 256 битам, возможна следующая схема расширения 128-битового блока в 256-битовый:
исходный блок:  ;
;
расширенный блок:
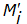
 ,
,
Код HMAC. Метод предполагает последовательное использование операций хеширования и шифрования с секретным ключом. При использовании для формирования НМАС быстродействующих специализированных хеш-функций (например, MD5, которая будет рассмотрена в разделе 3.10), быстродействие процедуры формирования контрольного кода можно существенно повысить, сохранив при этом все свойства, присущие MAC.




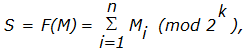
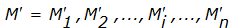
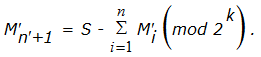
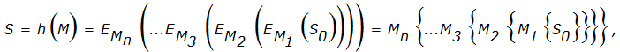
 .
.