Математическая модель рынка
1.2.6. Закон распределения промежутков между заявками на товар простейшего потока
Мы отмечали, что поток вызовов однозначно может быть определён
промежутками между заявками на товар  , а задаётся функцией распределения
, а задаётся функцией распределения  промежутков между поступлениями заявок на товар:
промежутков между поступлениями заявок на товар: 

Где  - моменты появления партий товаров.
- моменты появления партий товаров.
Вспомним также, что вероятность появления ровно  партий товара за время
партий товара за время 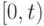 определяется выражением:
определяется выражением:

Отсюда вероятность того, что за промежуток 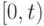 не поступит ни одна партия товара, то есть
не поступит ни одна партия товара, то есть 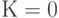 :
:
 , так как
, так как 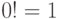 .
.
По определению под функцией распределения случайной величины zi
понимается вероятность того, то  :
:
 ,
, 
Это есть вероятность появления заявок на товар за время  (рис. 1.7) .
(рис. 1.7) .
Вероятность противоположного события:
 ,
, 
Это есть вероятность того, что за время  не появится ни одной заявки на товар. Так как простейший поток не обладает последействием, то появление в момент
не появится ни одной заявки на товар. Так как простейший поток не обладает последействием, то появление в момент 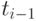 заявки на товар не влияет на появление заявки на товар в дальнейшем . Поэтому:
заявки на товар не влияет на появление заявки на товар в дальнейшем . Поэтому:

Отсюда: 
Функция распределения промежутков 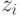 :
:
Дифференцируя по  , найдём плотность распределения случайной
, найдём плотность распределения случайной
величины 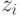 :
:
 (для
(для  )
)
Закон распределения случайной величины с такой плотностью
вероятности называется показательным (отрицательным экспоненциальным),
Марковским. Таким образом, простейший поток вызовов можно однозначно
задать либо:
 ,
, 
либо:


Вероятность того, что 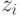 будет заключена между
будет заключена между  и
и  равна
равна

Математическое ожидание промежутка времени 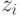 между двумя
между двумя
Поступлениями партий товаров:

Точнее:


Отсюда 
Предыдущий интеграл берётся по частям:
![\intop_{0}^{ \infty } t\cdot f(t)\cdot dt=\intop_{0}^{ \infty }u \cdot dv =[u\cdot v] |_0^\infty \intop_{0}^{ \infty }v \cdot du](/sites/default/files/tex_cache/b89bf2d0121edd26d6dd43430639046a.png)
Обозначим:

С учётом предыдущих обозначений, возьмём интеграл по частям:
![\intop_{0}^{ \infty } t \cdot f(t) \cdot dt=[-t\cdot \frac{1}{ \lambda } \cdot e^{- \lambda \cdot t}]|^{\infty}_0 - \intop_{0}^{ \infty }\frac{1}{ \lambda } \cdot e^{- \lambda \cdot t}=[-t \cdot \frac{1}{ \lambda }\cdot e^{-\lambda \cdot t}]|^{\infty}_0 + [-\frac{1}{ \lambda }\cdot e^{-\lambda \cdot t}]](/sites/default/files/tex_cache/c0a1ee73534a5e0f8138d847f3642b7d.png)
![-t\cdot \frac{1}{ \lambda }[\cdot e]^{ \uparrow }(- \lambda \cdot t])]|_{ \downarrow }0^{ \uparrow _{ \infty }}](/sites/default/files/tex_cache/1c64988cfbc82c9ba5e5d4ba69260fb4.png) - данное выражение содержит неопределённость
- данное выражение содержит неопределённость  , которая раскрывается по правилу Лопиталя (берётся производная от числителя и знаменателя).
, которая раскрывается по правилу Лопиталя (берётся производная от числителя и знаменателя).
Показательный закон обладает следующим замечательным свойством:
если промежуток времени, распределённый по показательному закону, уже длился некоторое время, то это не влияет на закон распределения оставшейся
части промежутка: он будет также показательным.
Следует отметить, что только показательный закон обладает этим
свойством. Это свойство представляет собой, фактически, другую формулировку для "отсутствия последействия", которое является основным
свойством простейшего потока.
Заканчивая рассмотрение свойств простейшего потока вызовов, следует
отметить, что потоки вызовов, которые создают заявки на товары в реальных условиях подчиняются свойствам простейшего потока только при условии, если эти потоки создаются бесконечно большим количеством источников нагрузки.
Однако достаточно точные результаты получаются при условии, если число источников нагрузки  на 2-3 порядка больше удельной интенсивности потока:
на 2-3 порядка больше удельной интенсивности потока: 
1.2.7. Длительность потребления. Поток освобождений
Длительность потребления поступившей партии товаров может быть постоянной, либо случайной.
Последовательность моментов окончания потребления товара образует
поток освобождений потребителя (группы потребителей). Свойства потока освобождений в общем случае зависят от свойств поступающего потока заявок на товар, функционирования рынка и закона распределения длительности потребления.
При постоянной длительности потребления и обслуживании всех заявок на товары без потерь свойства потока освобождений совпадают со свойствами потока поступления товаров. Происходит только сдвиг по времени на величину h между моментом поступления заявки на товар и моментом окончания его потребления.
При случайной длительности потребления, например, при потреблении участниками рынка, длительность потребления группы зависит от продолжительности потребления каждым участником группы. Наиболее простым и самым распространённым законом распределения длительности потребления является показательный.

 - вероятность освобождения одного группы потребителей за время
- вероятность освобождения одного группы потребителей за время  ,
,
где =- математическое ожидание длительности обслуживания
одной партии товаров,
 - параметр показательного закона.
- параметр показательного закона.
Вероятность  можно рассматривать как вероятность
можно рассматривать как вероятность
освобождения одного потребителя за время  .
.
Продолжительность потребления группы потребителей рынка достаточно хорошо описывается показательным распределением.
Найдём параметр потока освобождений при показательном законе
длительности потребления. Пусть в момент 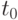 занято
занято  групп потребителей из
групп потребителей из  .
.
По определению параметра:

Здесь 
 есть вероятность освобождения за
есть вероятность освобождения за  хотя бы одной группы потребителей в предположении, что в момент
хотя бы одной группы потребителей в предположении, что в момент 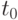 их было занято
их было занято  .
.
Эта вероятность равна 
Найдём 
 - вероятность того, что за
- вероятность того, что за  не освободится ни одного из
не освободится ни одного из  занятых устройств.
занятых устройств.
Вероятность не освобождения одного устройства за  :
:

Вероятность того, что не освободится и первое, и второе, … и  -е:
-е:

Вероятность того, что за  освободится хотя бы одно устройство при условии, что в момент времени
освободится хотя бы одно устройство при условии, что в момент времени 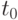 их было занято
их было занято  -ое :
-ое :
Вспомним ряд Маклорена:
 (принято, что
(принято, что 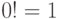 )
)

 , так как
, так как  есть бесконечно малая величина;
есть бесконечно малая величина;

Подставим это выражение в формулу для  :
:

Таким образом, параметр потока освобождений зависит от числа занятых
соединительных устройств и поток освобождений не является простейшим.

где  - число занятых устройств в момент
- число занятых устройств в момент 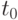 ,
,

 - параметр показательного закона,
- параметр показательного закона,
 - математическое ожидание длительности потребления.
- математическое ожидание длительности потребления.




