Математическая модель рынка

1. Математическая модель рынка

1.1. Определения

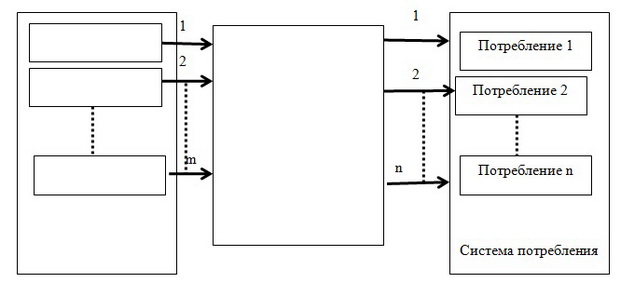
Для математической оценки процессов, происходящих в экономике необходимо создать модель, которая позволила бы отразить их в математическом виде и обеспечить количественный расчет, анализ и оценку возможного поведения системы Предлагаемая модель показана на рис. 1.1.

Рис. 1.1. Математическая модель рынка

Рынок содержит подсистемы, выполняющие следующие задачи.

Система производства - порождает случайный поток товаров (в общем случае отличающихся друг от друга). Под товаром понимается, любое изделие или услуга, предлагаемая для продажи, в которой имеется потребность, (в дальнейшем будет показано, как определить потребность в числовом виде). Это могут быть предметы питания, например, молоко и другие продукты питания, автомобили, дома, услуги по уборке дома, акции, строительные фирмы, предлагающие услуги по строительству домов и т.д.

Поток поступает в систему распределения.

Система распределения, может обслужить заказ немедленно или с какой-то задержкой. Задержка может быть двух типов:

• отказ в приёме товара из-за отсутствия спроса;
• или установка на ожидание реализации (накопление непроданных товаров)

Возможны два типа систем распределения.

Первые из них ставят задачу максимально быстро реализовать товар без всяких дополнительных условий. В теории массового обслуживания такая система распределения заявок на обслуживание называется полнодоступной, поскольку обеспечивает равный доступ к системе потребления и при расчётах поведения рынка - может не учитываться.

Системы второго типа распределяют товары, учитывая заданные приоритеты и ограничения для отдельных потребителей или систем потребления. Например, продажа табака, алкоголя, оружия … Системы этого типа называются неполнодоступными.

Если заказ принят, то система распределения пытается отдать его потребителям в систему потребления.

Система потребления обслуживает поток товаров. Это заключатся в том, что индивидуальные потребители или группы потребителей могут купить предложенные товар или отказаться от покупки.

Поступающий товар приобретается любой свободной группой потребителей. Занятой будем называть группу потребителей, которая за наблюдаемый период времени приобрела максимально возможную (или доступную) величину товаров и выбыла на некоторое время из потребления.

Если все группы потребителей заняты, то система потребления отказывается от приобретения товара, т.е. возникают потери.

При этом неприобретённый товар можно далее не предлагать, например, ликвидировать или система распределения может поставить его в очередь на ожидание реализации (накопление и сохранение непроданных товаров). В этом случае очень важно знать время ожидания. Оно может превысить разумное время (заданное время ожидания). В этом случае говорят об условных потерях. Поскольку товар доступен к продаже и через заданное время снимается с ожидания в соответствии с оговоренными условиями.

Если доля отказов от поступивших товаров превосходит определенную норму, то это свидетельствует о перепроизводстве, и требует мер по устранению таких потерь.

Заметим, что даже такая простая общая модель рынка имеет свои варианты.

Например, в данном случае мы рассматриваем, рынок, при котором производство и поставка товара (предложение) играет в системе роль входящего потока, а потери означают долю не проданного товара.

Практика показывает, что рынок может строиться, по принципу поступления на вход потока заявок на товары (плановая система), а потери заключатся в доле неудовлетворённых заявок спроса из-за отсутствия товаров.

Каждая из таких моделей имеет свои преимущества и недостатки, которые могут быть исследованы, но такие вопросы в курсе не рассмотрены. Рассматривается только система, где на рынок поступает предложение (поставка товаров), а спрос (потребители) его обслуживает.

Из рис.1.1 следует, что важным аспектом математической модели являются входные потоки. В соответствии с теорией обслуживания случайных потоков каждый входной поток может быть представлен математической моделью. Для определения типов случайных потоков далее используются определения из книг Лифшица и Стрельникова [4] , [8], [9],[24]. Понятия и методы теории массового обслуживания адаптируются к используемой модели рынка обслуживающей потоки товаров.

1.2. Основные понятия о потоках и типы входных потоков

1.2.1. Типы входных потоков

Потоком событий (в нашем случае товаров) называется последовательность предложений товаров поступающих через какие-либо интервалы или в какие-либо моменты времени.

Детерминированный поток событий - последовательность , в которой события поступают в определенные, строго фиксированные неслучайные моменты или через определенные, строго фиксированные, неслучайные промежутки времени. Например, продажа изделий с конвейера.

Случайный поток событий отличается от детерминированного тем и только тем, что моменты поставок товаров и промежутки времени между поставками являются не строго фиксированными, а случайными величинами. Детерминированные потоки являются частным случаем случайных потоков и на практике встречаются редко. Строго говоря, даже в таких потоках часто имеют место случайности. В связи с этим в теории массового облуживания потоков основное внимание уделяется рассмотрению случайных потоков вызовов.

Поток событий может быть определен одним или несколькими из трех эквивалентных способов:

1. последовательностью моментов наступления события ,

   Например, вероятность поступления конкретного товара в момент .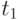

   Это может быть вероятность того, что мобильные телефоны будут поставляться в магазин каждую пятницу.

   В лотерее, это, например, вероятность выпадения цифры 6 в тиражах с номерами 5,7,15. При исследовании их можно обозначить как моменты .

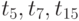2. Последовательностью промежутков времени между событиями моментами

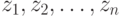
   Например, вероятность, что мобильные телефоны будут поставляться в магазин через каждые 7 дней.

   В лотерее, это, вероятность выпадения цифры 6 через каждые 5 тиражей.

3. Последовательностью чисел 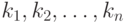, определяющих количество событий, поступающих в течение заданных отрезков времени .

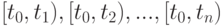   Например, вероятность, что в течение 15 месяцев (отсчитываемых от исходного момента свежая рыба поступит на продажу 5,6,.. 10 раз.