НОУ ИНТУИТ | Компьютерная математика с Maxima. Лекция 8: Реализация некоторых численных методов

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Компания ALT Linux

Опубликован: 24.03.2015 | Доступ: свободный | Студентов: 550 / 136 | Длительность: 19:00:00

Темы: Математика, Программное обеспечение, Физика

Специальности: Математик, Преподаватель, Физик

|

Вам нравится? Нравится 20 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

8.5 Решение обыкновенных дифференциальных уравнений

8.5.1 Методы решения задачи Коши

Среди задач, с которыми приходится иметь дело в вычислительной практике, значительную часть составляют различные задачи, сводящиеся к решению обыкновенных дифференциальных уравнений. Обычно приходится прибегать к помощи приближенных методов решения подобных задач. В случае обыкновенных дифференциальных уравнений в зависимости от того, ставятся ли дополнительные условия в одной или нескольких точках отрезка изменения независимой переменной, задачи обычно подразделяются на одноточечные (задачи с начальными условиями или задачи Коши) и многоточечные. Среди многоточечных задач наиболее часто в прикладных вопросах встречаются так называемые граничные задачи, когда дополнительные условия ставятся на концах рассматриваемого отрезка.

В дальнейшем ограничимся рассмотрением численных методов решения задачи Коши. Для простоты изложения методов решения задачи будем рассматривать случай одного обыкновенного дифференциального уравнения первого порядка.

Пусть на отрезке 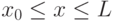$x_0 \leq x \leq L$ требуется найти решение 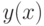y(x) дифференциального уравнения

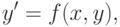( 8.6)

удовлетворяющее при x = x_0

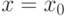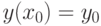начальному условию y(x_0) = y_0

.

Будем считать, что условия существования и единственности решения поставленной задачи Коши выполнены.

На практике найти общее либо частное решение задачи Коши удается для весьма ограниченного круга задач, поэтому приходится решать эту задачу приближенно.

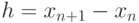Отрезок [x_0,L] накрывается сеткой (разбивается на интервалы) чаще всего с постоянным шагом ( $h = x_{n+1} - x_{n}$ ), и по какому- то решающему правилу находится значение 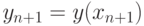$y_{n+1} = y(x_{n+1})$ . Таким образом, результатом решения задачи Коши численными методами является таблица, состоящую из двух векторов: 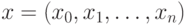$x = (x_0 , x_1 , \dots , x_n)$ — вектора аргументов и соответствующего ему вектора значений искомой функции $y = ( y_0 , y_1, \dots , y_n )$ .

Численные методы (правила), в которых для нахождения значения функции в новой точке используется информация только об одной (предыдущей) точке, называются одношаговыми.

Численные методы (правила), в которых для нахождения значения функции в новой точке используется информация о нескольких (предыдущих) точках, называются многошаговыми.

Из общего курса обыкновенных дифференциальных уравнений широкое распространение получил аналитический метод, основанный на идее разложения в ряд решения рассматриваемой задачи Коши. Особенно часто для этих целей используется ряд Тейлора. В этом случае вычислительные правила строятся особенно просто.

Приближенное решение 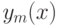y_m(x) исходной задачи ищут в виде

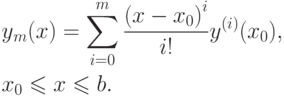$\begin{gathered} y{}_m(x) = \sum\limits_{i = 0}^m {\frac{{(x - x_0)}^i}{i!}} {y^{(i)}}(x_0), \hfill \\ {x_0} \leqslant x \leqslant b. \hfill \\ \end{gathered}$

( 8.7)

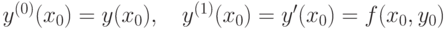Здесь ${y^{(0)}}(x_0) = y(x_0),\quad {y^{(1)}}(x_0) = y'(x_0) =f(x_0,y_0)$ , а значения 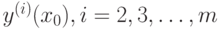$y^{(i)}(x_0), i = 2, 3, \dots , m$ находят по формулам, полученным последовательным дифференцированием заданного уравнения:

$\begin{gathered} y^{(2)}(x_0) = y''(x_0) = f_x(x_0,y_0) + f(x_0,y_0)f_y(x_0,y_0); \hfill \\ y^{(3)}(x_0) = y'''(x_0) = f_{x^2}(x_0,y_0) + 2f(x_0,y_0)f_y(x_0,y_0) + \hfill \\ + f^2(x_0,y_0)f_{y^2}(x_0,y_0) + f_y(x_0,y_0)[{f_x}({x_0},{y_0}) + f(x_0,y_0)f_y(x_0,y_0)];\hfill \\ \dots \hfill \\ y^{(m)}(x_0) = F_m(f;f_x;f_{x^2};f_{xy};f_{y^2};\dots ;f_{x^{m - 1}};f_{y^{m - 1}})|_{x = x_0,y = y_0}. \hfill \\ \end{gathered}$

( 8.8)

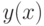Для значений , близких к x_0 , метод рядов (8.7) при достаточно большом значении дает обычно хорошее приближение к точному решению y(x) задачи (8.6). Однако с ростом расстояния 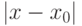|x - x_0| погрешность приближения искомой функции рядом возрастает по абсолютной величине (при одном и том же количестве членов ряда), и правило (8.7) становится вовсе неприемлемым, когда x выходит из области сходимости соответствующего ряда (8.7) Тейлора.

Если в выражении (8.7) ограничиться 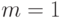m = 1 , то для вычисления новых значений 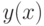y(x) нет необходимости пересчитывать значение производной, правда и точность решения будет невысока.

При использовании системы компьютерной алгебры более естественным выглядит метод последовательных приближений Пикара.

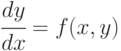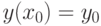Рассмотрим интегрирование единичного дифференциального уравнения $\cfrac{dy}{dx}=f(x,y)$ на отрезке [x_0,x] с начальным условием y(x_0) = y_0 . При формальном интегрировании получим:

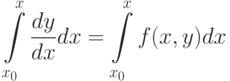
$\int\limits_{x_0}^{x}\frac{dy}{dx}dx=\int\limits_{x_0}^{x}f(x,y)dx$

Процедура последовательных приближений метода Пикара реализуется согласно следующей схеме

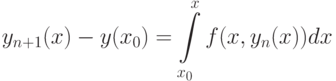
$y_{n+1}(x)-y(x_0)=\int\limits_{x_0}^{x}f(x,y_{n}(x))dx$

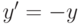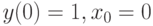В качестве примера рассмотрим решение уравнения y' = -y , при y(0) = 1, x_0 = 0 :

(%i1)	rp:-y$ y0:1$ x0:0$ /*rp-правая часть уравнения */
(%i4)	y1:y0+integrate(subst(y0,y,rp),x,x0,x);
	/* y1 - первое приближение */

$(\%o4)\ 1-x$

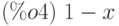
(%i5)	y2:y0+integrate(subst(y1,y,rp),x,x0,x);
	/* y2 - второе приближение */

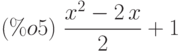
$(\%o5)\ \frac{{x}^{2}-2\,x}{2}+1$

(%i6)	y3:y0+integrate(subst(y2,y,rp),x,x0,x);

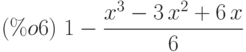
$(\%o6)\ 1-\frac{{x}^{3}-3\,{x}^{2}+6\,x}{6}$

(%i7)	expand(%); /* Очевидное решение рассматриваемого ОДУ -
		экспонента y=exp(-x).
		В результате использование метода Пикара
		получаем решение в виде ряда Тейлора */

$(\%o7)\ -\frac{{x}^{3}}{6}+\frac{{x}^{2}}{2}-x+1$

8.5.2 Метод рядов, не требующий вычисления производных правой части уравнения

Естественно поставить задачу о таком усовершенствовании приведенного выше одношагового метода, которое сохраняло бы основные его достоинства, но не было бы связано с нахождением значений производных правой части уравнения

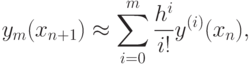$y_m(x_{n + 1}) \approx \sum\limits_{i = 0}^m \frac{h^i}{i!}y^{(i)}(x_n) ,$

( 8.9)

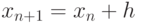где $x_{n+1} = x_n + h$ .

Чтобы выполнить это условие (последнее), производные y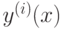 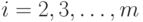$y^{(i)}(x)$ , $i = 2, 3, \dots , m$ , входящие в правую часть уравнения (8.9), можно заменить по формулам численного дифференцирования их приближенными выражениями через значение функции 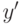и учесть, что y'(x) = f [x, y(x)] .

8.5.2.1 Метод Эйлера

В случае 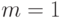m = 1 приближенное равенство (8.9) не требует вычисления производных правой части уравнения и позволяет с погрешностью порядка 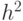h^2 находить значение 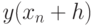y(x_n + h) решения этого уравнения по известному его значению y(x_n) . Соответствующее одношаговое правило можно записать в виде

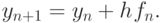$y_{n + 1} = y_n + h{\kern 1pt} f_n.$

( 8.10)

Это правило (8.10) впервые было построено Эйлером и носит его имя. Иногда его называют также правилом ломаных или методом касательных. Метод Эйлера имеет относительно низкий порядок точности — 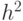h^2 на одном шаге. Практическая оценка погрешности приближенного решения может быть получена по правилу Рунге.

Пример реализации метода Эйлера средствами Maxima приведён в следующем примере:

(%i1)	euler1(rp,fun,y0,x0,xend,h):=block([OK,_x,_y,_y1,rez],
		_x:x0, _y:y0, rez:[_y], OK:-1, eps:0.1e-7,
		while OK<0 do (
			if ((_x+h>xend) or (abs(_x+h-xend)<eps))
				then (h:xend-_x,_x:xend, OK:1)
				else (_x:_x+h),
			_y1:makelist(float(_y[i]+h*subst([fun[i]=_y[i],x=_x],
				rp[i])),i,1,length(_y)),rez:append(rez,[_y1]),
			_y:_y1
		),
		rez
	)$

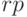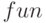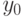Правые части решаемых дифференциальных уравнений передаются в функцию euler1 в списке . По умолчанию предполагается, что список имён зависимых переменных — fun , имя независимой переменной — . Начальные значения независимой и зависимых переменных — список y_0 и скалярная величина x_0 , граница интервала интегрирования — величина xend , шаг интегрирования — .

Следующий пример — обращение к функции euler1 . Приведено решение системы из трёх дифференциальных уравнений на интервале [0, 1] с шагом h = 0.1 :

$\left \{ {\begin{gathered} \frac{dy}{dx}=-2y,\\ \frac{dv}{dx}=-5v, \\ \frac{dz}{dx}=3x. \end{gathered}} \right.$

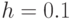С начальными условиями 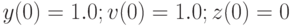y(0) = 1.0; v(0) = 1.0; z(0) = 0 , решением уравнений данной системы будут функции:

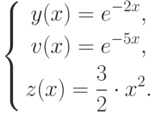
$\left \{ {\begin{gathered} y(x)=e^{-2x},\\ v(x)=e^{-5x},\\ z(x)=\frac{3}{2} \cdot x^2. \end{gathered}} \right.$

(%i2)	euler1([-2*y,-5*v,3*x],[y,v,z],[1,1,0],0,1,0.1);

$\begin{align*} &(\%o2)\ [[1,1,0],[0.8,0.5,0.03],[0.64,0.25,0.09],[0.512,0.125,0.18],\\ &[0.4096,0.0625,0.3],[0.32768,0.03125,0.45],[0.262144,0.015625,0.63],\\ &[0.2097152,0.0078125,0.84],[0.16777216,0.00390625,1.08],[0.134217728,\\ &0.001953125,1.35],[0.1073741824,9.7656249999999913*10^-4,1.65]] \end{align*}$

Проверить решение можно сравнивая графики точного решения и множества вычисленных приближенных значений. Пример последовательности команд, позволяющих выделить отдельные компоненты решения системы ОДУ и построить график точного и приближенного решения третьего уравнения системы, представлен ниже (точные решения — списки 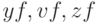yf, vf, zf ; приближенные решения — списки 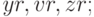yr, vr, zr; список значений независимой переменной — ).

(%i3)	rez:euler1([-2*y,-5*v,3*x],[y,v,z],[1,1,0],0,1.0,0.1)$
	n:length(rez)$
	yr:makelist(rez[k][1], k, 1, n)$
	vr:makelist(rez[k][2], k, 1, n)$
	zr:makelist(rez[k][3], k, 1, n)$
	xg:makelist(0.1*(k-1),k,1,n)$
	yf:makelist(exp(-2*xg[k]), k, 1, n)$
	vf:makelist(exp(-5*xg[k]), k, 1, n)$
	zf:makelist(3*xg[k]^2/2, k, 1, n)$
	plot2d ([[discrete, xg,zr],[discrete, xg,zf]],
			[style, points, lines])$

Уменьшение шага приводит к уменьшению погрешности решения (в данном примере — шаг 0.1).

Дальше >>

Авторизоваться

Компьютерная математика с Maxima

Реализация некоторых численных методов

8.5 Решение обыкновенных дифференциальных уравнений

8.5.1 Методы решения задачи Коши

8.5.2 Метод рядов, не требующий вычисления производных правой части уравнения

8.5.2.1 Метод Эйлера

Вопросы и ответы