НОУ ИНТУИТ | Компьютерная математика с Maxima. Лекция 8: Реализация некоторых численных методов

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Компания ALT Linux

Опубликован: 24.03.2015 | Доступ: свободный | Студентов: 550 / 136 | Длительность: 19:00:00

Темы: Математика, Программное обеспечение, Физика

Специальности: Математик, Преподаватель, Физик

|

Вам нравится? Нравится 20 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

8.5.2.2 Метод Рунге-Кутта

Изложим идею метода на примере задачи Коши:

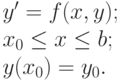
$y'=f(x,y); \\ {{x}_{0}}\le x\le b; \\ y({{x}_{0}})={{y}_{0}}. \\$

Интегрируя это уравнение в пределах от

до

(

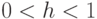), получим равенство

$y(x + h) = y(x) + \int\limits_x^{x + h} {f\,[t,y(t)]dt},$

( 8.10)

которое посредством последнего интеграла связывает значения решения рассматриваемого уравнения в двух точках, удаленных друг от друга на расстояние шага

.

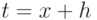Для удобства записи выражения (8.11) используем обозначение $\Delta y = y(x + h) - y(x)$ и замену переменной интегрирования t = x + h . Окончательно получим:

$\Delta y=h\int\limits_{0}^{1}{f[x}+\alpha \,h,y(x+\alpha \,h)]d\alpha \,$

( 8.12)

В зависимости от способа вычисления интеграла в выражении (8.12) получают различные методы численного интегрирования обыкновенных дифференциальных уравнений.

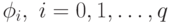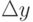Рассмотрим линейную комбинацию величин $\phi_i,\ i = 0, 1, \dots, q$ , которая будет являться аналогом квадратурной суммы и позволит вычислить приближенное значение приращения $\Delta y$ :

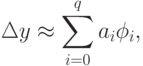
$\Delta y \approx \sum\limits_{i = 0}^q {{a_i}{\phi_i}} ,$

где

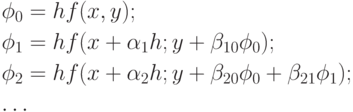
$\begin{gathered} {\phi _0} = hf(x,y); \hfill \\ {\phi _1} = hf(x + {\alpha _1}h;y + {\beta _{10}}{\phi _0}); \hfill \\ {\phi _2} = hf(x + {\alpha _2}h;y + {\beta _{20}}{\phi _0} + {\beta _{21}}{\phi _1}); \hfill \\ \dots \hfill \\ \end{gathered}$

Метод четвертого порядка для q = 3 , являющийся аналогом широко известной в литературе четырехточечной квадратурной формулы "трех восьмых", имеет вид

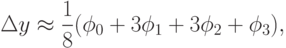
$\Delta y \approx \frac{1}{8}({\phi _0} + 3{\phi _1} + 3{\phi _2} + {\phi _3}),$

где

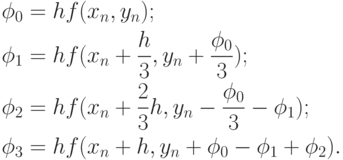
$\begin{gathered} {\phi _0} = hf({x_n},{y_n}); \hfill \\ {\phi _1} = hf({x_n} + \frac{h}{3},{y_n} + \frac{{{\phi _0}}}{3}); \hfill \\ {\phi _2} = hf({x_n} + \frac{2}{3}h,{y_n} - \frac{{{\phi _0}}}{3} - {\phi _1}); \hfill \\ {\phi _3} = hf({x_n} + h,{y_n} + {\phi _0} - {\phi _1} + {\phi _2}). \hfill \\ \end{gathered}$

Особо широко известно другое вычислительное правило типа Рунге-Кутта четвертого порядка точности:

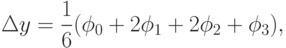
$\Delta y = \frac{1}{6}({\phi _0} + 2{\phi _1} + 2{\phi _2} + {\phi _3}),$

где

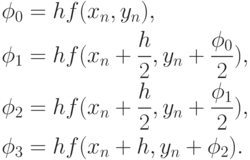
$\begin{gathered} {\phi _0} = hf({x_n},{y_n}), \hfill \\ {\phi _1} = hf({x_n} + \frac{h}{2},{y_n} + \frac{{{\phi _0}}}{2}), \hfill \\ {\phi _2} = hf({x_n} + \frac{h}{2},{y_n} + \frac{{{\phi _1}}}{2}), \hfill \\ {\phi _3} = hf({x_n} + h,{y_n} + {\phi _2}). \hfill \\ \end{gathered}$

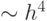Метод Рунге-Кутта имеет погрешность четвертого порядка ( $\sim h^4$ ).

Функция Maxima, реализующая метод Рунге-Кутта 4-го порядка, приведена в следующем примере (с печатью промежуточных результатов):

(%i1)	rk4(rp,fun,y0,x0,xend,h):=block(
		[OK,n,h1,_x,_y,_k1,_k2,_k3,_k4,rez],
		_x:x0, _y:y0, rez:[_y], OK:-1, h1:h, n:length(_y),
		while OK<0 do (
			if (_x+h1>=xend) then (h1:xend-_x, OK:1),
			_k1:makelist(float(h1*subst([fun[i]=
				float(_y[i]),x=float(_x)],rp[i])),i,1,n),
			_k2:makelist(float(h1*subst([fun[i]=
				float(_y[i]+_k1[i]/2),x=float(_x+h1/2)],
					rp[i])),i,1,n),
			_k3:makelist(float(h1*subst([fun[i]=
				float(_y[i]+_k2[i]/2),x=float(_x+h1/2)],
					rp[i])),i,1,n),
			_k4:makelist(float(h1*subst([fun[i]=
				float(_y[i]+_k3[i]),x=float(_x+h1)],rp[i])),
					i,1,n),
			_y1:makelist(float(_y[i]+
				(_k1[i]+2*_k2[i]+2*_k3[i]+_k4[i])/6),i,1,n),
			rez:append(rez,[_y1]),
			print("x= ",_x, " y= ",_y),
			_x:_x+h1,
			_y:_y1
		), rez
	)$

Пример обращения к функции rk4 представлен следующей последовательностью команд (решалась та же система, что и при тестировании метода Эйлера):

(%i2)	rk4([-2*y,-5*v,3*x],[y,v,z],[1,1,1],0,1,0.1);
x= 0	y= [1,1,1]
x= 0.1	y= [0.81873333333333,0.60677083333333,1.015]
x= 0.2	y= [0.67032427111111,0.36817084418403,1.06]
x= 0.3	y= [0.54881682490104,0.22339532993458,1.135]
x= 0.4	y= [0.44933462844064,0.13554977050718,1.24]
x= 0.5	y= [0.3678852381253,0.082247647208783,1.375]
x= 0.6	y= [0.30119990729446,0.04990547343658,1.54]
x= 0.7	y= [0.24660240409888,0.030281185705008,1.735]
x= 0.8	y= [0.20190160831589,0.018373740284549,1.96]
x= 0.9	y= [0.16530357678183,0.011148649703906,2.215]
x= 1.0	y= [0.13533954843051,0.0067646754713805,2.5]

Дальше >>

Авторизоваться

Компьютерная математика с Maxima

Реализация некоторых численных методов

8.5.2.2 Метод Рунге-Кутта

Вопросы и ответы