Реализация некоторых численных методов
8.4 Итерационные методы
В приближенных или итерационных методах решение системы линейных алгебраических уравнений является пределом итерационной последовательности, получаемой с помощью этих методов. К ним относятся: метод простой итерации, метод Зейделя и др. Итерационные методы выгодны для системы специального вида, со слабо заполненной матрицей очень большого вида порядка 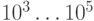 .
.
Для итерационных методов характерно то, что они требуют начальных приближений значений неизвестных, решение ищется в виде последовательности, постепенно улучшающихся приближений, и кроме того, итерационный процесс должен быть сходящимся. В вычислительной практике процесс итерации обычно продолжается до тех пор, пока два последовательных приближения не совпадут в пределах заданной точности.
8.4.1 Матричная формулировка итерационных методов решения систем линейных уравнений
При использовании СКМ Maxima вполне обосновано использование и матричной формулировки итерационных методов.
Рассмотрим решение системы 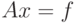 (
( — квадратная матрица,
— квадратная матрица,  — вектор правых частей,
— вектор правых частей,  — вектор неизвестных). Обозначим
— вектор неизвестных). Обозначим  , где
, где  — нижняя треугольная матрица с нулевыми диагональными элементами;
— нижняя треугольная матрица с нулевыми диагональными элементами;  — диагональная матрица;
— диагональная матрица;  — верхняя треугольная матрица с нулевыми диагональными элементами.
— верхняя треугольная матрица с нулевыми диагональными элементами.
Для решения этой системы рассмотрим итерационный процесс

 , или
, или
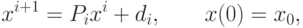
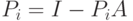 — оператор
— оператор  -го шага итерационного процесса;
-го шага итерационного процесса;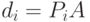 .
.Итерационный процесс сходящийся, если последовательность 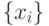 сходится к решению
сходится к решению  при любом
при любом  .
.
Если матрица не зависит от номера итерации, итерационный процесс называется стационарным:
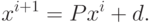 |
( 8.4) |
Необходимым и достаточным условием сходимости стационарного процесса является выполнение условия 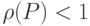 , где
, где 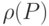 — спектральный радиус матрицы
— спектральный радиус матрицы  (наибольшее по модулю собственное число матрицы
(наибольшее по модулю собственное число матрицы  ).
).
С использованием введённых обозначений метод простой итерации (метод Якоби) даётся формулой:
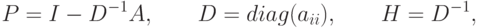
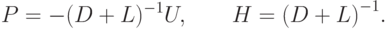
Рассмотрим поэлементные расчетные соотношения для методов Якоби и Гаусса—Зейделя.
Все элементы главной диагонали матрицы 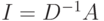 равны нулю, остальные элементы равны
равны нулю, остальные элементы равны 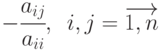 . Свободный член уравнения (8.4) равен
. Свободный член уравнения (8.4) равен 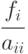 .
.
Таким образом, для метода Якоби итерационный процесс записывается в виде 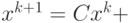 , где
, где 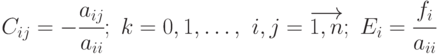 .
.
Для метода Гаусса–Зейделя 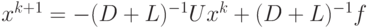 , или
, или 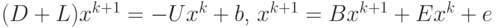 , где
, где
![B = \left[ {\begin{array}{*{20}{c}}
0&0&{\dots}&0 \\
{{c_{21}}}&0&{\dots}&0 \\
{{c_{31}}}&{{c_{32}}}&{\dots}&0 \\
{\dots}&{\dots}&{\dots}&{\dots} \\
{{c_{n - 1,1}}}&{{c_{n - 1,2}}}&{\dots}&0 \\
{{c_{n1}}}&{{c_{n2}}}&{\dots}&0
\end{array}} \right],
\text{и}\
E=\left[ \begin{matrix}
0 & {{c}_{21}} & \dots & \dots & {{c}_{1n}} \\
0 & 0 & \dots & \dots & {{c}_{2n}} \\
0 & {} & \ddots & {} & {} \\
\vdots & {} & {} & \ddots & {{c}_{n-1,n}} \\
0 & {} & {} & {} & 0 \\
\end{matrix} \right].](/sites/default/files/tex_cache/9919ae6edac1ac6fbc1bf69df13170ff.png)
Рассмотрим решение конкретной системы уравнений  методом Якоби:
методом Якоби:
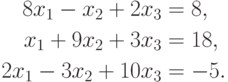
Вычисляем элементы матрицы  и вектора
и вектора  :
:
![B=\left[ \begin{matrix}
0 & \cfrac{1}{8} & -\cfrac{2}{8} \\
-\cfrac{1}{9} & 0 & -\cfrac{3}{9} \\
-0,2 & 0,3 & 0 \\
\end{matrix} \right],
\quad e = \left[ {\begin{array}{*{20}{c}}
1 \\
2 \\
{0,5}
\end{array}} \right] .](/sites/default/files/tex_cache/a12cb4558b50e863406c4d2547226608.png)
Вычислим значения x по формуле 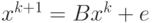 . Для решения использована следующая последовательность команд Maxima:
. Для решения использована следующая последовательность команд Maxima:
- преобразование заданных матриц
(%i1) A:matrix([8,-1,2],[1,9,3],[2,-3,10])$ b:matrix([8],[18],[5])$ A0:matrix([A[1,1],A[1,1],A[1,1]], [A[2,2],A[2,2],A[2,2]], [A[3,3],A[3,3],A[3,3]])$ B:-A/A0+diagmatrix(3,1)$ e:b/matrix([A[1,1]],[A[2,2]],[A[3,3]])$ x:e$
- собственно вычисление решения
(%i7) xt:float(B.x+e)$ xt:float(B.xt+e)$ xt:float(B.xt+e)$ xt:float(B.xt+e)$ xt:float(B.xt+e)$ xt:float(B.xt+e)$ xt:float(B.xt+e)$ x0:xt$ xt:float(B.xt+e)$ x1:xt$ r:x1-x0$ float(r); /* оценка сходимости*/ float(A.x1-b); /* оценка невязки*/
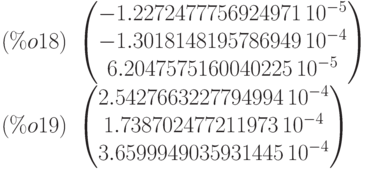
8.4.2 Метод простой итерации
Для решения системы линейных алгебраических уравнений (8.1) итерационным методом её необходимо привести к нормальному виду:
 |
( 8.5) |
Стационарное итерационное правило получаем, если матрица  и вектор
и вектор 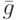 не зависят от номера итерации:
не зависят от номера итерации: 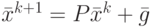 . Нестационарное итерационное правило получаем если матрица
. Нестационарное итерационное правило получаем если матрица  или вектор
или вектор 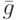 изменяются с ростом номера итерации:
изменяются с ростом номера итерации: 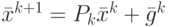 .
.
Стационарное итерационное правило обычно называют методом простой итерации. Предел итерационной последовательности является точным решением системы (8.5) или (8.1).
Для того, чтобы метод простой итерации сходился при любом начальном приближении, необходимо и достаточно, чтобы все собственные значения матрицы В были по модулю меньше единицы.
В силу того, что проверить сформулированное выше условие достаточно сложно на практике применяют следующие достаточные признаки:
- для того чтобы метод простой итерации сходился, достаточно, чтобы какая-либо норма матрицы
 была меньше единицы;
была меньше единицы; - для того чтобы метод простой итерации сходился, достаточно, чтобы выполнялось одно из следующих условий:
-
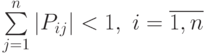 ;
; -
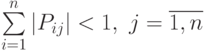 ;
; -
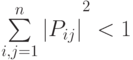 .
.
-
Для определения скорости сходимости можно воспользоваться следующей теоремой: если какая-либо норма матрицы  , согласованная с данной нормой вектора, меньше единицы, то имеет место следующая оценка погрешности метода простой итерации:
, согласованная с данной нормой вектора, меньше единицы, то имеет место следующая оценка погрешности метода простой итерации:
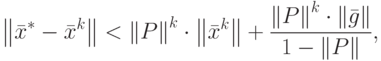
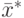 — точное решение системы (8.1).
— точное решение системы (8.1).Другими словами, условие сходимости выполняется, если выполняется условие доминирования диагональных элементов матрицы исходной системы  по строкам или столбцам:
по строкам или столбцам: 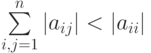 или
или  .
.
В этом случае легко можно перейти от системы вида (8.1) к системе (8.5). Для этого разделим  –ое уравнение системы на
–ое уравнение системы на 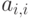 и выразим
и выразим  :
:
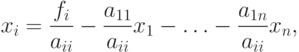
 будет выполнено одно из условий сходимости, где
будет выполнено одно из условий сходимости, где
![P=\left[ \begin{matrix}
0 & -\cfrac{{{a}_{12}}}{{{a}_{11}}} & \ldots &
-\cfrac{{{a}_{1n}}}{{{a}_{11}}}
\\
-\cfrac{{{a}_{21}}}{{{a}_{22}}} & 0 & \ldots &
-\cfrac{{{a}_{2n}}}{{{a}_{22}}}
\\
\ldots & \ldots & \ldots & \ldots \\
-\cfrac{{{a}_{n1}}}{{{a}_{nn}}} & -\cfrac{{{a}_{n2}}}{{{a}_{nn}}} & \ldots &
0
\\
\end{matrix} \right].](/sites/default/files/tex_cache/5d3513fc39ad1e3e07ab0fd768ce924e.png)
Пример реализации метода простой итерации средствами Maxima с печатью промежуточных результатов представлен в скрипте ниже:
(%i1) iterpr(a0,b0,x,n,eps):=block([a,b,x0,i,j,s,sum,p],
a:copymatrix (a0), b:copymatrix(b0), x0:copymatrix(x),
sum:1, p:0,
while sum>eps do (
sum:0, p:p+1, print("p= ",p," x= ",float(x)),
for i:1 thru n do (
s:b[i,1],
for j:1 thru n do (s:s-a[i,j]*x0[j,1]),
s:s/a[i,i], x[i,1]:x0[i,1]+s, sum:sum+abs(s)
),
x0:copymatrix(x)
),
float(x))$