НОУ ИНТУИТ | Компьютерная математика с Maxima. Лекция 8: Реализация некоторых численных методов

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Компания ALT Linux

Опубликован: 24.03.2015 | Доступ: свободный | Студентов: 550 / 136 | Длительность: 19:00:00

Темы: Математика, Программное обеспечение, Физика

Специальности: Математик, Преподаватель, Физик

|

Вам нравится? Нравится 20 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

8.2 Численное интегрирование

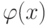Задача численного интегрирования состоит в замене исходной подинтегральной функции f(x) , для которой трудно или невозможно записать первообразную в аналитике, некоторой аппроксимирующей функцией $\varphi(x)$ . Такой функцией обычно является полином (кусочный полином) $\varphi (x) = \sum\limits_{i = 1}^n {{c_i}{\phi _i}(x)}$ .

Таким образом

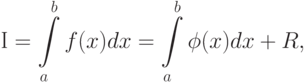
$\text{I}} = \int\limits_a^b {f(x)dx = \int\limits_a^b {\phi (x)dx + R},$

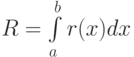где $R = \int\limits_a^b {r(x)dx}$ — априорная погрешность метода на интервале интегрирования, а r(x)

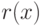— априорная погрешность метода на отдельном шаге интегрирования.

8.2.1 Обзор методов интегрирования

Методы вычисления однократных интегралов называются квадратурными (для кратных интегралов — кубатурными), и делятся на следующие группы:

Методы Ньютона-Котеса. Здесь 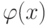$\varphi(x)$ — полином различных степеней. Сюда относятся метод прямоугольников, трапеций, Симпсона.
Методы статистических испытаний (методы Монте-Карло). Здесь узлы сетки для квадратурного или кубатурного интегрирования выбираются с помощью датчика случайных чисел, ответ носит вероятностный характер. В основном применяются для вычисления кратных интегралов.
Сплайновые методы. Здесь 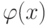$\varphi(x)$ — кусочный полином с условиями связи между отдельными полиномами посредством системы коэффициентов.
Методы наивысшей алгебраической точности. Обеспечивают оптимальную расстановку узлов сетки интегрирования и выбор весовых коэффициентов 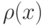$\rho(x)$ в задаче 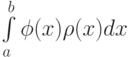$\int\limits_a^b {\phi (x)\rho (x)dx}$ (характерный пример — метод Гаусса).

8.2.2 Метод прямоугольников

Различают метод левых, правых и средних прямоугольников. Суть метода ясна из рисунка. На каждом шаге интегрирования функция аппроксимируется полиномом нулевой степени — отрезком, параллельным оси абсцисс.

Формулы метода прямоугольников можно получить из анализа разложения функции f(x) в ряд Тейлора вблизи некоторой точки x = x_i :

${\left. {f(x)} \right|_{x = {x_i}}} = f({x_i}) + \left( {x - {x_i}} \right)f'({x_i}) + \frac{{{{\left( {x - {x_i}} \right)}^2}}}{{2!}}f''({x_i}) + \dots.$

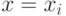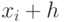Рассмотрим диапазон интегрирования от x_i до x_i + h , где — шаг интегрирования. Вычислим интеграл от исследуемой функции на этом промежутке:

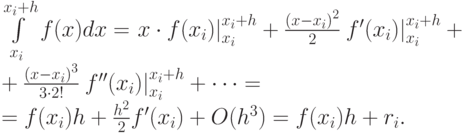
$&\int\limits_{x_i}^{{x_i} + h} f(x)dx = \left. {x \cdot f({x_i})} \right|_{{x_i}}^{{x_i} + h} + \frac{{{{\left( {x - {x_i}} \right)}^2}}}{2}\left. {f'({x_i})} \right|_{{x_i}}^{{x_i} + h} + \\ &+\frac{{{{\left( {x - {x_i}} \right)}^3}}}{{3 \cdot 2!}}\left. {f''({x_i})} \right|_{{x_i}}^{{x_i} + h} +\dots = \\ &=f({x_i})h + \frac{{{h^2}}}{2}f'({x_i}) + O({h^3})=f({x_i})h + {r_i}.$

таким образом, на базе анализа ряда Тейлора получена формула правых (или левых) прямоугольников и априорная оценка погрешности

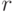на отдельном шаге интегрирования. Основной критерий, по которому судят о точности алгоритма — степень при величине шага в формуле априорной оценки погрешности. В случае равного шага

на всем диапазоне интегрирования общая формула имеет вид

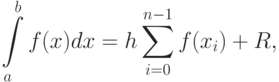
$\int\limits_a^b {f(x)dx = h\sum\limits_{i = 0}^{n - 1} {f({x_i}) + R} },$

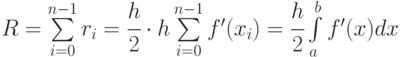где n — число разбиений интервала интегрирования, $R = \sum\limits_{i = 0}^{n - 1} {{r_i}} = \cfrac{h}{2} \cdot h\sum\limits_{i = 0}^{n - 1} {f'({x_i})} = \cfrac{h}{2}\int\limits_a^b {f'(x)dx}$ . Полученная оценка справедлива при наличии непрерывной производной подинтегральной функции f'(x)

.

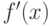8.2.3 Метод средних прямоугольников

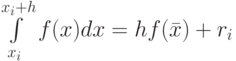Здесь на каждом интервале значение функции считается в средней точке отрезка [x_i,x_i + h] , то есть $\int\limits_{{x_i}}^{{x_i} + h} {f(x)dx =hf(\bar x) + {r_i}}$ .

Разложение функции в ряд Тейлора показывает, что в случае средних прямоугольников точность метода существенно выше:

$r = \frac{{{h^3}}}{{24}}f''(\bar x),{\text{ }}R = \frac{{{h^2}}}{{24}}\int\limits_a^b {f''(x)dx}.$

Пример функции Maxima, реализующей метод средних прямоугольников, представлен ниже:

(%i1)	intpr(f,n,a,b):=block([h,i,s,_x],h:(b-a)/n, _x:a+h/2, s:0,
	for i:1 thru n do (s:s+float(subst(_x,x,f)),_x:_x+h),s:s*h)$
(%i2)	intpr(x^2,100,-1,1);

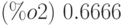
$(\%o2)\ 0.6666$

8.2.4 Метод трапеций

Аппроксимация в этом методе осуществляется полиномом первой степени. На единичном интервале

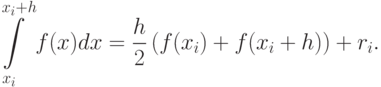
$\int\limits_{{x_i}}^{{x_i} + h} {f(x)dx = \frac{h}{2}\left( {f({x_i}) + f({x_i} + h)} \right) + {r_i}}.$

В случае равномерной сетки ( = const)

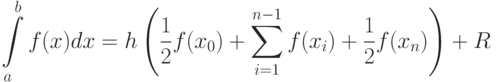
$\int\limits_a^b {f(x)dx = h\left( {\frac{1}{2}f({x_0}) + \sum\limits_{i = 1}^{n - 1} {f({x_i}) + \frac{1}{2}f({x_n})} } \right)} + R$

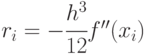При этом ${r_i} = - \cfrac{{{h^3}}}{{12}}f''({x_i})$ , а $R = -\cfrac{{{h^3}}}{{12}}\int\limits_a^b {f''(x)} dx$ .

Погрешность метода трапеций в два раза выше, чем у метода средних прямоугольников. Однако на практике найти среднее значение на элементарном интервале можно только у функций, заданных аналитически (а не таблично), поэтому использовать метод средних прямоугольников удаётся далеко не всегда. В силу разных знаков погрешности в формулах трапеций и средних прямоугольников истинное значение интеграла обычно лежит между двумя этими оценками.

Пример реализации метода трапеций в виде функции приведен ниже:

(%i1)	f:x^2;

$(\%o1)\ {x}^{2}$

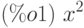
(%i2)	inttrap(f,n,a,b):=block([h,i,s],h:(b-a)/n,
	s:(float(subst(a,x,f))+float(subst(b,x,f)))/2,
	for i:1 thru n-1 do (s:s+float(subst(a+i*h,x,f))), s:s*h)$
(%i3)	inttrap(f,100,-1,1);

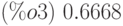
$(\%o3)\ 0.6668$

Подинтегральная функция задаётся в виде выражения Maxima. Выражение, определяющее подинтегральную функцию, можно задавать и непосредственно при обращении к методу, как в следующем примере:

(%i4)	inttrap(x*sin(x),100,-1,1);

$(\%o4)\ 0.60242947746101$

8.2.5 Метод Симпсона

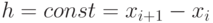При использовании данного метода подинтегральная функция f(x) заменяется интерполяционным полиномом второй степени P(x) — параболой, проходящей через три соседних узла. Рассмотрим два шага интегрирования ( $h = const = x_{i+1} - x_i$ ), то есть три узла 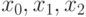x_0, x_1,x_2 , через которые проведем параболу, воспользовавшись уравнением Ньютона:

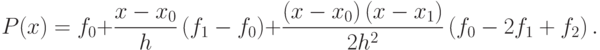
$P(x) = {f_0} + \frac{{x - {x_0}}}{h}\left( {{f_1} - {f_0}} \right) + \frac{{\left( {x - {x_0}} \right)\left( {x - {x_1}} \right)}}{{2{h^2}}}\left( {{f_0} - 2{f_1} + {f_2}} \right).$

Пусть 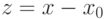z = x - x_0 , тогда

$P(z) &= {f_0} + \frac{z}{h}\left( {{f_1} - {f_0}} \right) + \frac{{z\left( {z - h} \right)}}{{2{h^2}}}\left( {{f_0} - 2{f_1} + {f_2}} \right) = \\ &= {f_0} + \frac{z}{{2h}}\left( { - 3{f_0} + 4{f_1} - {f_2}} \right) + \frac{{{z^2}}}{{2{h^2}}}\left( {{f_0} - 2{f_1} + {f_2}} \right)$

Воспользовавшись полученным соотношением, вычислим интеграл по данному интервалу:

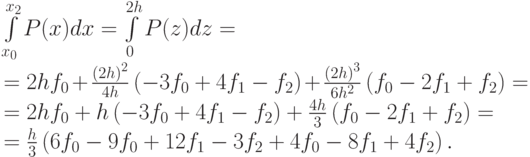
$&\int\limits_{{x_0}}^{{x_2}} {P(x)dx} = \int\limits_0^{2h}{P(z)dz} = \\ &=2h{f_0} + \frac{{(2h)}^2}{4h}\left( - 3{f_0} + 4{f_1} - {f_2}\right) + \frac{{(2h)}^3}{6h^2}\left({f_0} - 2{f_1} + {f_2}\right) = \\ &=2h{f_0} + h\left( - 3{f_0} + 4{f_1} - {f_2} \right) + \frac{{4h}}{3}\left({f_0} - 2{f_1} + {f_2}\right) = \\ &=\frac{h}{3}\left(6{f_0} - 9{f_0} + 12{f_1} - 3{f_2} + 4{f_0} - 8{f_1} + 4{f_2}\right).$

В итоге 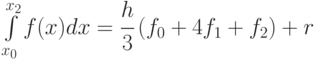$\int\limits_{{x_0}}^{{x_2}} {f(x)dx} = \cfrac{h}{3} \left({f_0} +4{f_1} + {f_2} \right) + r$ .

Для равномерной сетки и чётного числа шагов n формула Симпсона принимает вид:

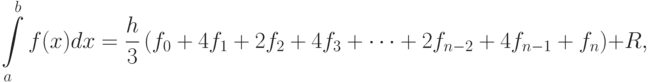
$\int\limits_a^b {f(x)dx} = \frac{h}{3} \left( {f_0} + 4{f_1} + 2{f_2} + 4{f_3} + \dots + 2{f_{n - 2}} + 4{f_{n - 1}} + {f_n}\right) + R,$

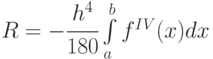где $r = - \cfrac{h^5}{90}{f^{IV}}({x_i})$ , а $R = -\cfrac{h^4}{180}\int\limits_a^b {f^{IV}(x)dx}$ в предположении непрерывности четвёртой производной подинтегральной функции.

Реализация метода Симпсона средствами Maxima представлена в следующем примере:

(%i1)	intsimp(f,n,a,b):=block([h,h2,i,_x,s],h:(b-a)/n, h2:h/2,
	s:(float(subst(a,x,f))+float(subst(b,x,f)))/2+
				2*float(subst(a+h2,x,f)),
	_x:a,
	for i:1 thru n-1 do (_x:_x+h,
		s:s+2*float(subst(_x+h2,x,f))+float(subst(_x,x,f))),
	s:s*h/3)$
(%i2)	intsimp(x^2,100,-1,1);

$(\%o2)\ 0.66666666666667$

Дальше >>

Авторизоваться

Компьютерная математика с Maxima

Реализация некоторых численных методов