Моделирование с Maxima
6.2.4 Расчёт коэффициентов линейной регрессии
Коэффициенты и оценка статистической значимости для простейшей линейной регрессии могут оцениваться при помощи функции  из пакета stats. Функция вычисляет коэффициенты и параметры линейной регрессии
из пакета stats. Функция вычисляет коэффициенты и параметры линейной регрессии 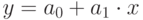 (т.е. только простейшей).
(т.е. только простейшей).
Синтаксис вызова:  или
или  .
.
Опции функции  (уровень значимости, обычно 0.95, см. выше) и
(уровень значимости, обычно 0.95, см. выше) и  (по умолчанию
(по умолчанию  , имя независимой переменной). Рассматриваемая функция выводит большое количество статистических параметров:
, имя независимой переменной). Рассматриваемая функция выводит большое количество статистических параметров:
- 'model: полученное уравнение регрессии;
- 'means: среднее;
- 'variances: дисперсии обоих переменных;
- 'correlation: коэффициент корреляции;
- 'adc: коэффициент детерминации;
-
'a_estimation: оценка параметра
 ;
; -
'a_conf_int: доверительный интервал для
 ;
; -
 оценка параметра b;
оценка параметра b; -
'b_conf_int: доверительный интервал для
 ;
; -
'hypotheses: нулевая и альтернативная гипотеза относительно параметра
 ;
; - 'statistic: статистические характеристики выборки, использованные для проверки нулевой гипотезы;
- 'distribution: распределение выборки;
-
'p_value: величина вероятности для проверки гипотезы о статистической значимости
 ;
; - 'v_estimation: оценка остаточной дисперсии;
- 'v_conf_int: доверительный интервал для остаточной дисперсии
- 'cond_mean_conf_int: доверительный интервал для среднего;
- 'new_pred_conf_int: доверительный интервал для нового предсказания;
- 'residuals: список, содержащий остатки.
По умолчанию на консоль выводятся только параметры 1, 4, 14, 9, 10, 11, 12, и 13 в этом списке. Остальные параметры скрыты, но доступ к ним обеспечивается при помощи функций  или
или  .
.
Задаёмся исходными данными
(%i9) s:[[125,140.7], [130,155.1], [135,160.3], [140,167.2], [145,169.8]]$
Вычисляем коэффициенты и прочие параметры регрессии
(%i10) z:simple_linear_regression(s,conflevel=0.99);
![\begin{pmatrix}
SIMPLE\ LINEAR\ REGRESSION\cr
model=1.405999999999986\ x-31.18999999999804\cr
correlation=0.96116852552552\cr
v\_estimation=13.57966666666665\cr
b\_conf\_int=[0.044696336625253,2.767303663374718]\cr
hypotheses=H0: b = 0,\ H1: b \symbol{`\#} 0\cr
statistic=6.032686683658114\cr
distribution=[student\_t,3]\cr
p\_value=0.0038059549413203
\end{pmatrix}\leqno{(\%o10) }](/sites/default/files/tex_cache/2793d74c0aff60fb730b79186ffccab1.png)
(%i11) z:simple_linear_regression(s,conflevel=0.95);
![\begin{pmatrix}
SIMPLE\ LINEAR\ REGRESSION\cr
model=1.405999999999986\ x-31.18999999999804\cr
correlation=0.96116852552552\cr
v\_estimation=13.57966666666665\cr
b\_conf\_int=[0.66428743645021,2.147712563549759]\cr
hypotheses=H0: b = 0,\ H1: b \symbol{`\#} 0\cr
statistic=6.032686683658114\cr
distribution=[student\_t,3]\cr
p\_value=0.0038059549413203
\end{pmatrix}\leqno{(\%o11) }](/sites/default/files/tex_cache/0d3765440ff7fc29226eaa09ef37bab2.png)
Некоторые дополнительные параметры:
(%i5) take_inference(model,z), x=133;

(%i6) take_inference(means,z);
![[135.0,158.62]\leqno{(\%o6) }](/sites/default/files/tex_cache/0e55835271def2dc3cbe5c5f719db4f9.png)
(%i7) take_inference(new_pred_conf_int,z), x=133;
![[132.0728595995113,179.5431404004887]\leqno{(\%o7) }](/sites/default/files/tex_cache/c58c685866c61eb0db108b9fe77af38f.png)
Графическая иллюстрация построенной линейной зависимости см. на рис.6.5. Использованная команда:
(%i11) plot2d([[discrete,s], take_inference(model,z)], [x,120,150],[style,[points],[lines]],[gnuplot_term,ps], [gnuplot_out_file, "regress.eps"])$
6.2.5 Использование метода наименьших квадратов
Пакет Maxima включает мощный модуль для линейного и нелинейного оценивания параметров различных моделей с использованием метода наименьших квадратов — пакет lsqares.
Основная функция пакета lsqares — это функция  .
.
Синтаксис вызова: 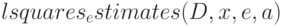 или
или 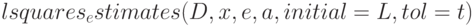
Функция предназначена для оценки параметров, лучше всего соответствующих уравнению  в переменных
в переменных  и
и  по набору данных D, которые определяются методом методом наименьших квадратов. Функция
по набору данных D, которые определяются методом методом наименьших квадратов. Функция  сначала пытается отыскать точное решение, и если это не удаётся, ищет приблизительное решение. Возвращаемое значение — список вида
сначала пытается отыскать точное решение, и если это не удаётся, ищет приблизительное решение. Возвращаемое значение — список вида ![[a = ... , b = ... , c = ... ]](/sites/default/files/tex_cache/d9ce226995c09bbe358bf89f7e24a5db.png) . Элементы списка обеспечивают минимум среднеквадратичной ошибки. Данные
. Элементы списка обеспечивают минимум среднеквадратичной ошибки. Данные  должны быть матрицей. Каждый ряд — одна запись или один случай, каждый столбец соответствует значениям некоторой переменной.
должны быть матрицей. Каждый ряд — одна запись или один случай, каждый столбец соответствует значениям некоторой переменной.
Список переменных  дает название для каждого столбца
дает название для каждого столбца  (даже для столбцов, которые не входят в анализ). Список параметров содержит названия параметров, для которых отыскиваются оценки. Уравнение
(даже для столбцов, которые не входят в анализ). Список параметров содержит названия параметров, для которых отыскиваются оценки. Уравнение  является выражением или уравнением в переменных
является выражением или уравнением в переменных  и
и  ; если
; если  записано не в форме уравнения, его рассматривают как уравнение
записано не в форме уравнения, его рассматривают как уравнение 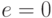 . Если некоторое точное решение может быть найдено при помощи
. Если некоторое точное решение может быть найдено при помощи  , данные
, данные  могут содержать и нечисловые значения.
могут содержать и нечисловые значения.
Дополнительные аргументы  определены как уравнения и передаются "дословно" функции
определены как уравнения и передаются "дословно" функции 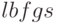 , которая используется, чтобы найти оценки численным методом, когда точный результат не найден. Однако, если никакое точное решение не найдено, у каждого элемента
, которая используется, чтобы найти оценки численным методом, когда точный результат не найден. Однако, если никакое точное решение не найдено, у каждого элемента  должно быть числовое значение, в том числе константы (такие как
должно быть числовое значение, в том числе константы (такие как  и
и  ) или числовые литералы (целые числа, рациональные, с плавающей точкой, и с плавающей точкой повышенной точности). Численные расчеты выполняются с обычной арифметикой с плавающей точкой, таким образом все другие виды чисел преобразуются к значениям с плавающей точкой. Для работы с
) или числовые литералы (целые числа, рациональные, с плавающей точкой, и с плавающей точкой повышенной точности). Численные расчеты выполняются с обычной арифметикой с плавающей точкой, таким образом все другие виды чисел преобразуются к значениям с плавающей точкой. Для работы с  необходимо загрузить эту функцию командой load(
необходимо загрузить эту функцию командой load( ).
).
Пример (точное решение):
(%i1) load (lsquares)$ (%i2) M:matrix([1,1,1],[3/2,1,2],[9/4,2,1],[3,2,2],[2,2,1]);
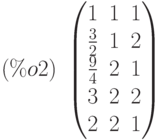
(%i3) lsquares_estimates(M,[z,x,y],(z+D)^2=A*x+B*y+C,[A,B,C,D]);
![(\%o3)\ [[A=-\frac{59}{16},B=-\frac{27}{16},C=\frac{10921}{1024},D=-\frac{107}{32}]]](/sites/default/files/tex_cache/5f2fcd4c545a45eb4fbed230a8af2ca8.png)
Другой пример (точное решение отсутствует, отыскивается приближенное):
(%i1) load (lsquares)$ M : matrix ([1, 1], [2, 7/4], [3, 11/4], [4, 13/4]);
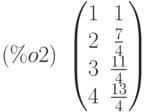
(%i3) lsquares_estimates(M,[x,y],y=a*x^b+c,[a,b,c],initial=[3,3,3], iprint=[-1,0]);
![(\%o3)\ [[a=1.375751433061394,b=.7148891534417651,\\
c=-.4020908910062951]]](/sites/default/files/tex_cache/d5b951d4ac114fd0adf1cd60d35cf1e3.png)
Для расчёта невязок для уравнения  при подстановке в него данных, содержащихся в матрице
при подстановке в него данных, содержащихся в матрице  , можно использовать функцию
, можно использовать функцию 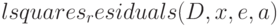 (смысл параметров тот же, что и для функции
(смысл параметров тот же, что и для функции  ).
).
Пример использования функции  и
и 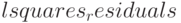 (те же данные, что использованы для расчёта параметров простой линейной регрессии):
(те же данные, что использованы для расчёта параметров простой линейной регрессии):
(%i1) load (lsquares)$ (%i2) s:[[125,140.7],[130,155.1],[135,160.3],[140,167.2],[145,169.8]];
![(\%o2)\ [[125,140.7],[130,155.1],[135,160.3],[140,167.2],[145,169.8]]](/sites/default/files/tex_cache/67c2d57ef02123ed8e31d99aeb3321bb.png)
(%i3) D:apply(matrix,s);

(%i4) a : lsquares_estimates(D,[y,x],y = A+B*x, [A,B]);
![[[A=\frac{8231525}{267474},B=\frac{87875}{133737}]]\leqno{(\%o4) }](/sites/default/files/tex_cache/2c142e4e3e79a68958e95d997938ed38.png)
(%i5) float(%);
![[[A=30.77504729431646,B=0.65707321085414]]\leqno{(\%o5) }](/sites/default/files/tex_cache/f09526fd989fcfe152f44c3262399012.png)
(%i6) lsquares_residuals (D, [y,x], y = A + B*x, first(a));
![(\%o6)\ [1.774751938506171,-2.687102297793416,-1.103882994234965,\\
-0.63768814912851,2.653921502650718]](/sites/default/files/tex_cache/8a09202a60540df5df3ea186a1679609.png)
Остальные функции, входящие в состав пакета lsquares, по синтаксису использования и идее реализации аналогичны приведенным (см. документацию разработчика).

