Моделирование с Maxima
6.2 Статистические методы анализа данных
6.2.1 Ввод-вывод матричных данных
Для чтения и записи матричных или потоковых данных в составе Maxima предусмотрен пакет numericalio.
Функции пакета рассчитаны на ввод/вывод данных, каждое поле которых предполагается атомом (в смысле Lisp), т.е. целых чисел, чисел с плавающей точкой, строк или символов. Атомы воспринимаются numericalio так же, как при интерактивном вводе в консоли или выполнении batch-файла. Возможно использование различных символов-сепараторов для разделения полей данных (параметр  ).
).
Основные функции пакета numericalio:
-
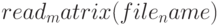 (другие формы вызова —
(другие формы вызова —  ). Функция
). Функция  считывает матрицу из файла. Здесь
считывает матрицу из файла. Здесь  — имя файла, из которого считываются данные,
— имя файла, из которого считываются данные,  — имя потока. Если не указан
— имя потока. Если не указан  , данные предполагаются разделёнными пробелами. Функция возвращает считанный объект.
, данные предполагаются разделёнными пробелами. Функция возвращает считанный объект. -
 (другие формы —
(другие формы —  ) — считывает список из файла или из потока.
) — считывает список из файла или из потока. -
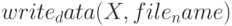 (другие формы —
(другие формы —  ) — осуществляет вывод объекта
) — осуществляет вывод объекта  (списка, матрицы, массива Lisp или Maxima и др.) в файл file_name (или объекта X в поток S). Матрицы выводятся по столбцам и строкам с использованием пробела или другого символаразделителя (см.
(списка, матрицы, массива Lisp или Maxima и др.) в файл file_name (или объекта X в поток S). Матрицы выводятся по столбцам и строкам с использованием пробела или другого символаразделителя (см.  ).
).
Наряду с указанными простыми функциями, используются более специфичные: 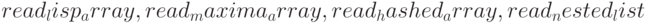 , предназначенные для считывания массивов в формате Lisp или Maxima, особенности применения которых не рассматриваются в данной книге.
, предназначенные для считывания массивов в формате Lisp или Maxima, особенности применения которых не рассматриваются в данной книге.
6.2.2 Функции Maxima для расчёта описательной статистики
Система Maxima содержит ряд функций для выполнения статистических расчётов (описательной статистики), объединённые в пакет descriptive. Функции, входящие в состав descriptive, позволяют выполнить расчёт дисперсии, среднеквадратичного отклонения, медианы, моды и т.п. Названия функций и краткое описание выполняемых ими действий приведены в табл. 6.1.
| Функция | Выполняемые действия | Синтаксис вызова и примечания |
|---|---|---|
 |
Вычисление среднего |
 или или 
|
 |
Вычисление среднего геометрического |
 или или 
|
 |
Вычисление среднего гармонического |
 или или 
|
 |
Вычисляет корреляционную матрицу |
 или или  равна равна 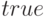 или или 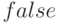 (при расчёте по ковариационной матрице) (при расчёте по ковариационной матрице) |
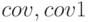 |
Вычисляет ковариационную матрицу | 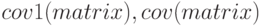 |
 |
Вычисляет медиану |  |
 |
Вычисляет среднеквадратичное отклонение (корень квадратный из  или или  ) ) |
аналогично 
|
 |
Вычисляет дисперсию случайной величины |  |
 |
Вычисляет центральный момент порядка 
|
 |
 |
Вычисляет момент порядка 
|
 |
 |
Вычисление асимметрии |  |
 |
Вычисление эксцесса |  |
 |
Вычисление  -квантиля -квантиля |
quantile(list, p), quantile(matrix, p) |
 |
Выбор наибольшего и наименьшего значения в выборке соответственно | 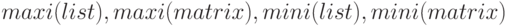 |
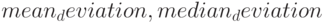 |
Сумма абсолютных отклонений от среднего или медианы соответственно | Аналогично 
|
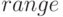 |
Размах вариации выборки |  |
 |
Возвращает список, включающий две матрицы — матрицу, обратную ковариационной, и матрицу частных коэффициентов корреляции |
 , где , где  равна равна 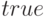 или или  (при расчёте по ковариационной матрице) (при расчёте по ковариационной матрице) |
 |
Аналог функции submatrix | |
 |
Возвращает список, содержащий различные виды дисперсии |  |
Построение графических иллюстраций производится при помощи функций  (непосредственная визуализация данных),
(непосредственная визуализация данных),  (строит гистограмму),
(строит гистограмму), 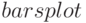 (также строит гистограмму, но по дискретным или нечисловым данным),
(также строит гистограмму, но по дискретным или нечисловым данным),  (график Бокса- Вискера),
(график Бокса- Вискера),  (круговая диаграмма). Синтакисис вызова и параметры функций во многом аналогичны компонентам пакета draw (см. примеры ниже).
(круговая диаграмма). Синтакисис вызова и параметры функций во многом аналогичны компонентам пакета draw (см. примеры ниже).
Основные общие опции (унаследованные от draw):
- terminal — устройство, на которое выводится диаграмма (возможные значения — eps и png, по умолчанию диаграмма выводится на экран, другие варианты);
- file_name — имя файла, в который выводить гистограмму (расширение устанавливается по опции terminal)
- title — основной заготовок;
- xlabel, ylabel — названия (метки) осей,
Рассмотрим пример использования функций пакета descriptive для статистической обработки массивов данных. Данные берем из файлов, входящих в состав пакета descriptive (файлы biomed.data, wind.data и др.). Перед началом работы загружаем необходимые пакеты descriptive и numericalio. При помощи функции  считывается матрица, содержащая 100 строк и 5 столбцов.
считывается матрица, содержащая 100 строк и 5 столбцов.
(%i1) load(descriptive)$ load(numericalio)$
s:read_matrix (file_search ("wind.data"))$
length(s);
(%o4) 100
(%i5) mean(s); /* рассчитываем среднее значение. При обработке
матрицы получаем список средних по столбцам.*/![[9.948499999999999,10.1607,10.8685,15.7166,14.8441]\leqno{(\%o5) }](/sites/default/files/tex_cache/10582160b75718465b4bcbf48c34aa7e.png)
(%i6) median(s);
![[10.06,9.855,10.73,15.48,14.105]\leqno{(\%o6) }](/sites/default/files/tex_cache/f66fb67998a1477ac85f8601715ca56b.png)
(%i7) var(s);
![(\%o7)\ [17.22190675000001,14.98773651000001,15.47572875,\\
32.17651044000001,24.42307619000001]](/sites/default/files/tex_cache/bfbceea0c64d686f4847939c6e2ebf4a.png)
(%i8) std(s);
![(\%o8)\ [4.149928523480858,3.871399812729242,3.933920277534866,\\
5.672434260526957,4.941970881136392]](/sites/default/files/tex_cache/bc6811efd7b27b97dd8d11e300dc35f5.png)
(%i9) mini(s);
![[0.58,0.5,2.67,5.25,5.17]\leqno{(\%o9) }](/sites/default/files/tex_cache/c5467f8f5e86e520c9fcc496a20623fe.png)
(%i10) maxi(s);
![[20.25,21.46,20.04,29.63,27.63]\leqno{(\%o10) }](/sites/default/files/tex_cache/9ffa36acf4d0d0f80063d0d3c390b4dd.png)
(%i11) mini(%); /* При обработке списка и поиске в нём минимального элемента получаем одно значение! */
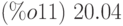
Для построения диаграмм разброса (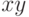 -диаграмм) предназначена функция
-диаграмм) предназначена функция  . Синтаксис вызова:
. Синтаксис вызова:

Данные для функции  могут представляться вектором (списком) или матрицей. Одномерные массивы рассматриваются как временные ряды с равноотстоящими точками.
могут представляться вектором (списком) или матрицей. Одномерные массивы рассматриваются как временные ряды с равноотстоящими точками.
Основные опции, специфичные для данной функции:
- point_size — размер точки на графике (целое положительное число);
- point_type — вид точки (отсутствие точек — none (-1), dot (0), plus (1), multiply (2), asterisk (3), square (4), filled_square (5), circle (6), filled_circle (7), up_triangle (8), filled_up_triangle (9), down_triangle (10), filled_down_triangle (11), diamant (12), filled_diamant (13));
- color — цвет точки (тот же набор цветов, что и в пакете draw);
-
grid — наличие сетки на графике (
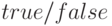 ).
).
Для построения гистограмм используется функция  (синтаксис вызова аналогичен
(синтаксис вызова аналогичен  и основные опции идентичны опциям
и основные опции идентичны опциям  ). Рассмотрим дополнительные опции, специфичные для
). Рассмотрим дополнительные опции, специфичные для  :
:
- nclasses (по умолчанию 10) — число классов гистограммы, или список с указанием пределов классов и их число, или только пределы;
- frequency — указывает масштаб шкалы ординат, возможные значения: абсолютный, относительный и процентный (default, absolute, persent);
- htics (default, auto) — формат промежуточных делений на гистограмме, возможные значения — auto, endpoints, intervals, или список меток;
При построении гистограммы доступны также локальные и глобальные опции пакета draw.
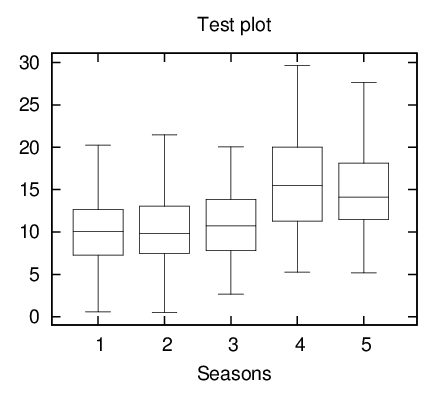
Для графического представления описательной статистики служит диаграмма Бокса-Уискера ("ящик-с-усами"), которая является удобным способом наглядно представить статистические данные пятью параметрами: наименьшее и наибольшее значения выборки, нижний, средний и верхний квартили. На данной диаграмме могут быть показаны и выбросы (если они есть).
Для построения диаграмм Бокса-Уискера используется функция  . Синтаксис вызова:
. Синтаксис вызова:  или
или  .
.
Параметр  — список или матрица с несколькими столбцами. Опции функции
— список или матрица с несколькими столбцами. Опции функции  идентичны опциям
идентичны опциям  .
.
Столбчатые диаграммы (обычно частотные) строятся для данных, разбитых на категории, при помощи функции 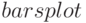 . Эти диаграммы позволяют графически отобразить различия между данными категорий.
. Эти диаграммы позволяют графически отобразить различия между данными категорий.
Достаточно распространённым способом графического изображения структуры статистических совокупностей является секторная диаграмма, так как идея целого очень наглядно выражается кругом, который представляет всю совокупность. Относительная величина каждого значения изображается в виде сектора круга, площадь которого соответствует вкладу этого значения в сумму значений. Этот вид графиков строится в Maxima функцией  .
.
Рассмотрим примеры использования графических утилит пакета descriptive.
Для дальнейшего использования считываем данные из файла wind.data (это тестовый файл в составе пакета descriptive, содержит матрицу 100х5).
(%i1) load(descriptive)$ load(numericalio)$
s:read_matrix (file_search("wind.data"))$
(%i4) x:makelist(s[k][1],k,1,length(s))$
(%i5) y:makelist(s[k][2],k,1,length(s))$
(%i6) m:makelist([x[k],y[k]],k,1,100)$
(%i7) xy:apply('matrix,m)$Строим график (точечный) зависимости  от
от  (см. рис.6.1). Результаты сохраняются в файле maxima_out.eps (имя файла — по умолчанию, он создаётся в домашнем каталоге пользователя). Необходимые команды:
(см. рис.6.1). Результаты сохраняются в файле maxima_out.eps (имя файла — по умолчанию, он создаётся в домашнем каталоге пользователя). Необходимые команды:
(%i8) scatterplot(xy,terminal=eps);
Считывая данные из файла pidigits.data, строим гистограмму частотного распределения десятичных знаков числа ? (см. рис.6.2). Результаты сохраняются в файле histogram.eps (имя файла задаётся опцией file_name = "histogram", он создаётся в домашнем каталоге пользователя). Необходимые команды:
load (descriptive)$ s1 : read_list (file_search ("pidigits.data"))$
histogram (s1, nclasses=8, title="pi digits", xlabel="digits",
ylabel="Absolute frequency", fill_color=grey, fill_density=0.6,
terminal=eps, file_name="histogram")$Следующий пример — график Бокса-Уискера с аннотациями по осям (см. рис.6.3). Необходимые команды (результат сохраняется в файле boxwisker.eps, англоязычные наименования заменены на русские переводы):
(%i10) boxplot(s,title = "Test plot", xlabel = "Seasons", terminal=eps,file_name="boxwisker")$
Пример построения столбчатой диаграммы с использованием функции 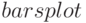 — на рис.6.4. График построен командой (результат сохраняется в файл barsplot.eps):
— на рис.6.4. График построен командой (результат сохраняется в файл barsplot.eps):
load (descriptive)$ l1:makelist(random(8),k,1,50)$ l2:makelist(random(8),k,1,100)$ barsplot(l1,l2, box_width=1/2, fill_density=3/4,sample_keys=["A","B"], bars_colors=[grey10,grey50], terminal=eps, file_name="barsplot")$
Основные опции команды 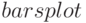 :
:
- box_width — относительная ширина прямоугольников (по умолчанию 3/4, величина в пределах [0, 1]);
- grouping — индикатор, показывающий, как представляются множественные образцы (возможные значения clustered и stacked);
- groups_gap — натуральное число, представляющее разрыв между двумя соседними группами (относительная величина, по умолчанию 1);
- bars_colors — список цветов для множественных образцов (по умолчанию [ ]);
-
start_at — указывает начало графика по оси
 (по умолчанию 0).
(по умолчанию 0).
С функцией 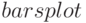 можно использовать и опции пакета draw.
можно использовать и опции пакета draw.
Для построения круговых (секторных) диаграмм используется функция  .
.
Пример использования  :
:
load (descriptive)$
s1 : read_list (file_search ("pidigits.data"))$
piechart(s1, xrange=[-1.1, 1.3], yrange=[-1.1, 1.1],
title="Digit frequencies in pi")$Цвета секторов и радиус диаграммы описываются опциями sector_colors и pie_radius.
К сожалению, базовая программа вывода графики Maxima — gnuplot — написана очень давно, и воспринимает кириллические символы только в кодировках KOI8-R или KOI8-U (в последних версиях — и utf8). Возможным решением (принятым для построения графиков в этой книге) является создание файла .gnuplot, содержащего следующие команды: set encoding koi8r или set encoding utf8.
Однако и в этом случае может возникнуть необходимость в редактировании файла maxout.gnuplot, содержащего команды для построения последнего графика.