НОУ ИНТУИТ | Компьютерная математика с Maxima. Лекция 6: Моделирование с Maxima

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Компания ALT Linux

Опубликован: 24.03.2015 | Доступ: свободный | Студентов: 550 / 136 | Длительность: 19:00:00

Темы: Математика, Программное обеспечение, Физика

Специальности: Математик, Преподаватель, Физик

|

Вам нравится? Нравится 20 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

6.2.3 Проверка статистических гипотез

Для проверки статистических гипотез в Maxima включён пакет stats. Он позволяет, в частности, проводить сопоставление средних или дисперсий двух выборок. Предусмотрена и проверка нормальности распределения, а также ряд других стандартных тестов. для использования stats пакет необходимо загрузить командой load("stats"); необходимые пакеты descriptive и distrib загружаются автоматически.

Функции пакета stats возвращают данные типа inference_result . Объекты этого типа содержат необходимые результаты для анализа статистических распределений и проверки гипотез.

Функция позволяет оценить среднее значение и доверительный интервал по выборке. Синтаксис вызова: test_mean () или test_mean ( x, option_1, option_2, ... ).

Функция test_mean использует проверку по критерию Стьюдента. Аргумент — список или одномерная матрица с тестируемой выборкой. Возможно также использование центральной предельной теоремы (опция asymptotic ). Опции test_mean :

'mean, по умолчанию 0, ожидаемое среднее значение;
'alternative, по умолчанию 'twosided, вид проверяемой гипотезы (возможные значения 'twosided, 'greater и 'less);
'dev, по умолчанию 'unknown, величина среднеквадратичного отклонения, если оно известно ('unknown или положительное выражение);
'conflevel, по умолчанию 95/100, уровень значимости для доверительного интервала (величина в пределах от 0 до 1);
'asymptotic, по умолчанию 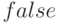, указывает какой критерий использовать (-критерий или центральную предельную теорему).

Результаты, которые возвращает функция:

'mean_estimate — среднее по выборке;
'conf_level — уровень значимости, выбранный пользователем;
'conf_interval — оценка доверительного интервала;
'method — использованная процедура;
'hypotheses — проверяемые статистические гипотезы (нулевая и альтернативная );
'statistic — число степеней свободы для проверки нулевой гипотезы;
'distribution — оценка распределения распределения выборки;
'p_value — вероятность ошибочного выбора гипотезы , если выполняется .

Примеры использования test_mean :

Выполняется -тест с неизвестной дисперсией. Нулевая гипотеза H_0 : среднее равно 50 против альтернативной гипотезы H_1 : среднее меньше 50; в соответствии с результатами расчёта, величина вероятности слишком велика, чтобы отвергнуть H_0 .

(%i1)	load("stats")$
(%i2)	data: [78,64,35,45,45,75,43,74,42,42]$
(%i3)	test_mean(data,'conflevel=0.9,'alternative='less,'mean=50);

$(\%o3)\ \begin{pmatrix} MEAN\ TEST\cr mean\_estimate=54.3\cr conf\_level=0.9\cr conf\_interval=[-\infty ,61.51314273502714]\cr method=Exact\ t-test.\ Unknown\ variance.\cr hypotheses=H0:\ mean = 50 ,\ H1:\ mean < 50\cr statistic=.8244705235071678\cr distribution=[student\_t,9]\cr p\_value=.7845100411786887 \end{pmatrix}$

Следующий тест — проверка гипотезы H_0 (среднее равно 50) против альтернативной гипотезы H_1 среднее по выборке отлично от 50. В соответствии с величиной p << 1 нулевая гипотеза. Данный тест применяется для больших выборок.

(%i1)	load("stats")$
(%i2)	test_mean([36,118,52,87,35,256,56,178,57,57,89,34,25,98,35,
		98,41,45,198,54,79,63,35,45,44,75,42,75,45,45,
		45,51,123,54,151],'asymptotic=true,'mean=50);

$(\%o2)\ \begin{pmatrix} MEAN\ TEST\cr mean\_estimate=74.88571428571429\cr conf\_level=0.95\cr conf\_interval=[57.72848600856193,92.04294256286664]\cr method=Large\ sample\ z-test.\ Unknown\ variance.\cr hypotheses=H0:\ mean = 50 ,\ H1:\ mean\ \#\ 50\cr statistic=2.842831192874313\cr distribution=[normal,0,1]\cr p\_value=.004471474652002261 \end{pmatrix}$

Функция test_means_difference позволяет проверить, принадлежат ли выборки x_1 и x_2 к одной генеральной совокупности.

Синтаксис вызова: test_means_difference(x_1,x_2) или t est_means_difference(x_1,x_2,option_1,option_2,...) .

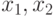Данная функция выполняет t-тест для сравнения средних по выборкам x_1 и x_2 ( x_1, x_2 — списки или одномерные матрицы). Сравнение выборок может проводиться также на основании центральной предельной теоремы (для больших выборок). Опции функции test_means_difference такие же, как и для , кроме оценок среднеквадратичных отклонений выборок (если они известны) Список опций:

'alternative, по умолчанию 'twosided, вид проверяемой гипотезы (возможные значения 'twosided, 'greater и 'less);
'dev1, 'dev2, по умолчанию 'unknown, величины среднеквадратичных отклонений для выборок и , если они известны ('unknown или положительное выражение);
'conflevel, по умолчанию 95/100, уровень значимости для доверительного интервала (величина в пределах от 0 до 1);
'asymptotic, по умолчанию 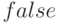, указывает какой критерий использовать (-критерий или центральную предельную теорему).

Вывод результатов test_means_difference не отличается от вывода результатов .

Примеры использования test_means_difference : Для двух малых выборок проверяется гипотеза H_0 от равенстве средних против альтернативной гипотезы H_1 : различие математических ожиданий статистически значимо, т.е. выборки принадлежат к разным генеральным совокупностям.

(%i1)	load("stats")$
(%i2)	x: [20.4,62.5,61.3,44.2,11.1,23.7]$
(%i3)	y: [1.2,6.9,38.7,20.4,17.2]$
(%i4)	 test_means_difference(x,y,'alternative='greater);

$(\%o4)\ \begin{pmatrix} DIFFERENCE\ OF\ MEANS\ TEST\cr diff\_estimate=20.31999999999999\cr conf\_level=0.95\cr conf\_interval=[-.04597417812881588,\infty ]\cr method=Exact\ t-test.\ Welch\ approx.\cr hypotheses=H0:\ mean1 = mean2 ,\ H1:\ mean1 > mean2\cr statistic=1.838004300728477\cr distribution=[student\_t,8.62758740184604]\cr p\_value=.05032746527991905 \end{pmatrix}$

Оценка доверительного интервала для дисперсии выборки проводится при помощи функции test_variance .

Синтаксис вызова: test_variance(x) или test_variance(x,option_1,option_2,...)

Данная функция использует тест 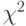$\chi^2$ . Предполагается, что распределение выборки нормальное. Опции функции test_variance :

'mean, по умолчанию 'unknown, оценка математического ожидания (среднее по выборке), если оно известно;
'alternative, по умолчанию 'twosided, вид проверяемой гипотезы (возможные значения 'twosided, 'greater и 'less);
'variance, по умолчанию 1, это оценка дисперсии выборки для сравнения с фактической дисперсией;
'conflevel, по умолчанию 95/100, уровень значимости для доверительного интервала (величина в пределах от 0 до 1).

Основной результат, возвращаемый функцией — оценка дисперсии выборки var_estimate и доверительный интервал для неё.

Пример: Проверка, отличается ли дисперсия выборки с неизвестным математическим ожиданием от значения 200.

(%i1)	load("stats")$
(%i2)	x: [203,229,215,220,223,233,208,228,209]$
(%i3)	test_variance(x,'alternative='greater,'variance=200);

$(\%o3)\ \begin{pmatrix} VARIANCE\ TEST\cr var\_estimate=110.75\cr conf\_level=0.95\cr conf\_interval=[57.13433376937479,\infty ]\cr method=Variance\ Chi-square\ test.\ Unknown\ mean.\cr hypotheses=H0:\ var\ =\ 200 ,\ H1:\ var\ >\ 200\cr statistic=4.430000000000001\cr distribution=[chi2,8]\cr p\_value=.8163948512777688 \end{pmatrix}$

Сравнение дисперсий двух выборок проводится при помощи функции test_variance (синтаксис вызова test_variance_ratio(x_1,x_2) или test_variance_ratio(x_1,x_2,option_1,option_2,...) .

Данная функция предназначена для сопоставления дисперсий двух выборок с нормальным распределением по критерию Фишера (-тест). Аргументы x_1 и x_2 — списки или одномерные матрицы, содержащие независимые выборки.

Опции функции test_variance_ratio :

'mean1, 'mean2, по умолчанию 'unknown, оценки математических ожиданий выборок и , если они известны;
'alternative, по умолчанию 'twosided, вид проверяемой гипотезы (возможные значения 'twosided, 'greater и 'less);
'conflevel, по умолчанию 95/100, уровень значимости для доверительного интервала (величина в пределах от 0 до 1).

Основной результат, возвращаемый функцией test_variance_ratio — отношение дисперсий выборок ratio_estimate .

Пример: проверяется гипотеза о равенстве дисперсий двух выборок по сравнению с альтернативной гипотезой о том, что дисперсия первой больше, чем дисперсия второй.

(%i1)	load("stats")$
(%i2)	x: [20.4,62.5,61.3,44.2,11.1,23.7]$
(%i3)	y: [1.2,6.9,38.7,20.4,17.2]$
(%i4)	test_variance_ratio(x,y,'alternative='greater);

$(\%o4)\ \begin{pmatrix} VARIANCE\ RATIO\ TEST\cr ratio\_estimate=2.316933391522034\cr conf\_level=0.95\cr conf\_interval=[.3703504689507263,\infty ]\cr method=Variance\ ratio\ F-test.\ Unknown\ means.\cr hypotheses=H0:\ var1\ =\ var2 ,\ H1:\ var1\ >\ var2\cr statistic=2.316933391522034\cr distribution=[f,5,4]\cr p\_value=.2179269692254463 \end{pmatrix}$

При отсутствии представлений о распределении выборки может использоваться непараметрический тест для сравнения средних. Оценка медианы непрерывной выборки проводится при помощи функции test_sign . Синтаксис вызова test_sign(x) или test_sign(x,option_1,option_2,...) .

Функция test_sign допускает две опции: alternative (аналогично test_mean ) и median (по умолчанию 0, или оценка значения медианы для проверки статистической значимости).

Результаты, которые возвращает функция:

'med_estimate: медиана выборки;
'method: использованная процедура;
'hypotheses: проверяемые статистические гипотезы (нулевая и альтернативная );
'statistic: число степеней свободы для проверки нулевой гипотезы;
'distribution: оценка распределения распределения выборки;
'p_value: вероятность ошибочного выбора гипотезы , если выполняется .

Пример: проверка гипотезы H_0 о равенстве медианы выборки 6, против альтернативной гипотезы H_1 : медиана больше 6.

(%i1)	load("stats")$
(%i2)	x: [2,0.1,7,1.8,4,2.3,5.6,7.4,5.1,6.1,6]$
(%i3)	test_sign(x,'median=6,'alternative='greater);

$(\%o3)\ \begin{pmatrix} SIGN\ TEST\cr med\_estimate=5.1\cr method=Non\ parametric\ sign\ test.\cr hypotheses=H0:\ median\ =\ 6 ,\ H1:\ median\ >\ 6\cr statistic=7\cr distribution=[binomial,10,0.5]\cr p\_value=.05468749999999989 \end{pmatrix}$

Аналогичная функция — test_signed_rank(x) (либо с указанием опций test_signed_rank(x,option_1,option_2,...) ), которая использует тест правила знаков Вилкоксона для оценки гипотезы о медиане непрерывной выборки. Опции и результаты функции такие же, как и для функции test_sign .

Пример: проверка гипотезы H_0 : медиана равна 15 против альтернативной гипотезы H_1 : медиана больше 15.

(%i1)	load("stats")$
(%i2)	x: [17.1,15.9,13.7,13.4,15.5,17.6]$
(%i3)	test_signed_rank(x,median=15,alternative=greater);

$(\%o3)\ \begin{pmatrix} SIGNED\ RANK\ TEST\cr med\_estimate=15.7\cr method=Exact test\cr hypotheses=H0:\ med\ =\ 15 ,\ H1:\ med\ >\ 15\cr statistic=14\cr distribution=[signed\_rank,6]\cr p\_value=0.28125 \end{pmatrix}$

Непараметрическое сравнение медиан двух выборок реализовано в одной функции — test_rank_sum . В данной функции используется тест Вилкоксона-Манна-Уитни. -критерий Манна-Уитни — непараметрический метод проверки гипотез, часто использующийся в качестве альтернативы -тесту Стьюдента. Обычно этот тест используется для сравнения медиан двух распределений x_1 и x_2 , не являющихся нормальными (отсутствие нормальности не позволяет применить - тест).

Синтаксис вызова: test_rank_sum(x_1,x_2) или test_rank_sum(x_1,x_2,option_1) .

Функция допускает лишь одну опцию: alternative (аналогично test_means_difference ).

Результаты, которые возвращает функция:

'method: использованная процедура;
'hypotheses: проверяемые статистические гипотезы (нулевая и альтернативная );
'statistic: число степеней свободы для проверки нулевой гипотезы;
'distribution: оценка распределения распределения выборки;
'p_value: вероятность ошибочного выбора гипотезы , если выполняется .

Пример: проверка, одинаковы ли медианы выборок x_1 и x_2 .

(%i1)	load("stats")$
(%i2)	x:[12,15,17,38,42,10,23,35,28]$
(%i3)	y:[21,18,25,14,52,65,40,43]$
(%i4)	test_rank_sum(x,y);

$(\%o4)\ \begin{pmatrix} RANK\ SUM\ TEST\cr method=Exact\ test\cr hypotheses=H0:\ med1 = med2 ,\ H1:\ med1\ \#\ med2\cr statistic=22\cr distribution=[rank\_sum,9,8]\cr p\_value=.1995886466474702 \end{pmatrix}$

Для выборок большего объёма распределение выборок приблизительно нормальное. Сравниваем гипотезы H_0 : медиана 1 = медиана 2 и H_1 : медиана 1 < медиана 2.

(%i1)	load("stats")$
(%i2)	x: [39,42,35,13,10,23,15,20,17,27]$
(%i3)	y: [20,52,66,19,41,32,44,25,14,39,43,35,19,56,27,15]$
(%i4)	test_rank_sum(x,y,'alternative='less);

$(\%o4)\ \begin{pmatrix} RANK\ SUM\ TEST\cr method=Asymptotic\ test.\ Ties\cr hypotheses=H0:\ med1 = med2 ,\ H1:\ med1\ <\ med2\cr statistic=48.5\cr distribution=[normal,79.5,18.95419580097078]\cr p\_value=.05096985666598441 \end{pmatrix}$

Проверка нормальности распределения осуществляется функцией test_normality(x) . В этой функции реализован тест Шапиро-Уилка. Выборка (список или одномерная матрица) должна быть размером не менее 2, но не более 5000 элементов (иначе выдаётся сообщение об ошибке). Функция возвращает два значения: statistic — величина -статистики и величина вероятности (если больше принятого уровня значимости, нулевая гипотеза о нормальности распределения выборки не отвергается). Статистика характеризует близость выборочного распределения к нормальному (чем ближе к 1, тем меньше вероятность ошибочно принять гипотезу о нормальности распределения).

Пример: проверка гипотезы о нормальном распределения генеральной совокупности по заданной выборке.

(%i1)	load("stats")$
(%i2)	x:[12,15,17,38,42,10,23,35,28]$
(%i3)	test_normality(x);

$(\%o3)\ \begin{pmatrix} SHAPIRO\ -\ WILK\ TEST\cr statistic=.9251055695162439\cr p\_value=.4361763918860427 \end{pmatrix}$

Дальше >>

Авторизоваться

Компьютерная математика с Maxima

Моделирование с Maxima

6.2.3 Проверка статистических гипотез

Вопросы и ответы