Функция распределения случайной величины. Виды распределения
Сравнение экспериментальных распределений с нормальным законом
Для того чтобы сравнивать любое экспериментальное распределение с нормальным, выполняют стандартизацию распределения по следующему несложному алгоритму.
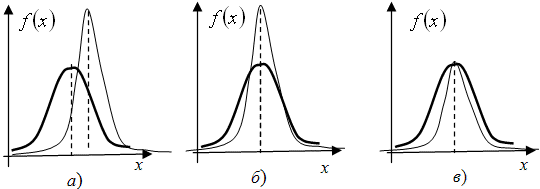
1. Строят графики функций распределения экспериментального и нормального рядов в едином масштабе, после чего совмещают эти графики наложением друг на друга, начиная с нулевой точки
2. Может случиться так, что линии 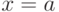 для нормального ряда и
для нормального ряда и 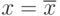 для экспериментаьлного совпадут, как на рис.9.15б . Тогда данный пункт алгоритма следует опустить и сразу перейти к следующему. Но если эти линии не совпадают (рис.9.15а ), то тогда от каждого элемента экспериментального ряда отнимают, если
для экспериментаьлного совпадут, как на рис.9.15б . Тогда данный пункт алгоритма следует опустить и сразу перейти к следующему. Но если эти линии не совпадают (рис.9.15а ), то тогда от каждого элемента экспериментального ряда отнимают, если  (прибавляют, если
(прибавляют, если  ) величину, равную
) величину, равную 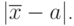 Эта операция называется центрированием. Она позволяет совместить на одной прямой максимумы построенных функций (рис.9.15 б). Таким образом в результате данного шага от исходного экспериментального ряда переходят к
Эта операция называется центрированием. Она позволяет совместить на одной прямой максимумы построенных функций (рис.9.15 б). Таким образом в результате данного шага от исходного экспериментального ряда переходят к
![\[ x_{i}^*= x_{i}-|\overline x-a| \ или \ x_{i}^*=x_{i}+|\overline x-a|. \]](/sites/default/files/tex_cache/e044fdb2eb06ec1d6a266b50b26fb17b.png) |
( 26) |
3. Завершают процедуру стандартизации ряда операцией нормировки на рассеяние (рис.9.15в ) по формуле
![\[ z_{i}=\frac {x_{i}^*} {\sigma}=\frac {x_{i}-|\overline x-a|} {\sigma } \ или \ z_{i}=\frac {x_{i}^*} {\sigma}=\frac {x_{i}+|\overline x-a|} {\sigma }.\]](/sites/default/files/tex_cache/c19a281fb02b5b478daae17d1e1af4c3.png) |
( 27) |
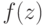 в силу своих особенностей, которые здесь не обсуждаются, получила название кумулятивной функции распределения.
в силу своих особенностей, которые здесь не обсуждаются, получила название кумулятивной функции распределения.Если построенное нормальное распределение 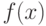 имеет
имеет 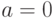 и
и 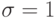 , то график называют нормированным, а функция
, то график называют нормированным, а функция 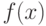 обладает всеми свойствами нормированной кривой. Такие функции широко используются для расчетов теоретических кривых распределений. А сама
обладает всеми свойствами нормированной кривой. Такие функции широко используются для расчетов теоретических кривых распределений. А сама 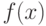 выглядит следующим образом
выглядит следующим образом
![\[ f(x)= -\frac 1 {\sqrt{2\pi}} e^{-\frac {x^2} 2} \]](/sites/default/files/tex_cache/4ee6279bbefbed02033ada18a67611e6.png) |
( 28) |
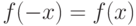 .
.Для того чтобы определить, находится ли экспериментальная величина в границах таких, как если бы она была бы нормально распределена, исследуют кумулятивную функцию распределения, больше известную как функцию Лапласа
![\[ \Phi(z)=\frac 2 {\sqrt{2\pi}}\int\limits_{-\infty}^{z}e^{-\frac {z^2} 2}dz \]](/sites/default/files/tex_cache/51db0848bcb97a6351b652ca8c99a757.png) |
( 29) |
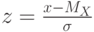 .
Тогда на основании свойства 2 интегральной функции распределения, вероятность того, что случайная величина попадет в интервал
.
Тогда на основании свойства 2 интегральной функции распределения, вероятность того, что случайная величина попадет в интервал ![$[x_{1};x_{2}]$](/sites/default/files/tex_cache/5190e9c3154b12816596d989ff6e7d55.png) определиться из
определиться из![\[ P(x_{1} \leqslant x \leqslant x_{2})=\frac 1 2 \left (\Phi(x_{2})-\Phi(x_{1}) \right ), \]](/sites/default/files/tex_cache/718fd5211d460518abf8e12ddd97ae32.png) |
( 30) |
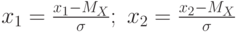 .
.Из равенства (30) и свойства 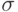 можно сформулировать правило 3-х сигм, известное как критерий Чебышева.
можно сформулировать правило 3-х сигм, известное как критерий Чебышева.
Правило 3-х сигм (критерий Чебышева). Если случайная величина распределена по нормальному закону, то отклонение этой величины от математического ожидания ряда не превосходит  влево и вправо от
влево и вправо от 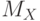 .
.
Это правило на практике используется как необходимое условие для того, чтобы данный экспериментальный ряд был распределен по нормальному закону. Это значит что, если правило  не выполняется, то ряд экспериментальных данных не подчиняется нормальному закону распределения. Но это утверждение не всегда верно в "обратную сторону", т.е. если правило
не выполняется, то ряд экспериментальных данных не подчиняется нормальному закону распределения. Но это утверждение не всегда верно в "обратную сторону", т.е. если правило  выполняется, то ряд экспериментальных данных подчиняется нормальному закону распределения. Иными словами, выполнение этого правила не гарантирует, что исследуемый ряд распределен нор-мально. Необходимы дополнительные исследования ряда.
выполняется, то ряд экспериментальных данных подчиняется нормальному закону распределения. Иными словами, выполнение этого правила не гарантирует, что исследуемый ряд распределен нор-мально. Необходимы дополнительные исследования ряда.
Пример 3. Установлено, что при измерении диаметра валика микрометром случайная погрешность измерений подчиняется нормальному закону распределения со средним квадратическим отклонением 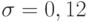 мм. Систематической погрешностью пренебрегаем. Найти вероятность того, что измерения проводились с ошибкой не более, чем
мм. Систематической погрешностью пренебрегаем. Найти вероятность того, что измерения проводились с ошибкой не более, чем 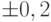 мм.
мм.
Решение. Определим 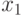 для формулы (30). Данное значение 0,2 – это среднее отклонение
для формулы (30). Данное значение 0,2 – это среднее отклонение 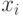 конкретного измерения от математического ожидания, следовательно,
конкретного измерения от математического ожидания, следовательно, 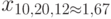 . О наименьшем значении
. О наименьшем значении 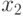 ничего в задаче не сказано, поэтому примем его равным нулю, т.е. измерения выполнялись вообще без погрешностей. Тогда с учетом сказанного, получаем
ничего в задаче не сказано, поэтому примем его равным нулю, т.е. измерения выполнялись вообще без погрешностей. Тогда с учетом сказанного, получаем
![\[P \left ( |x| < 0,2 \right )=\Phi \left ( \frac {0,2} {0,12}\right ) =\Phi \left (1,67 \right ) = 0,9051 \]](/sites/default/files/tex_cache/274f153d63e39d72e5700655b21fd235.png) |
( 31) |
Значение функции 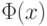 для конкретного
для конкретного 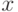 берется из специальных таблиц.
берется из специальных таблиц.
Биноминальное распределение
Биноминальным распределением называется функция распределения вероятностей появления 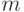 событий в
событий в 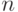 независимых испытаниях, в каждом из которых вероятность появления события постоянна и равна
независимых испытаниях, в каждом из которых вероятность появления события постоянна и равна 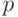 :
:
![\[p(x=m)=C_{n}^m p^m q^{n-m} \]](/sites/default/files/tex_cache/ff050eed44dbbf7ae030dc6cbf4079e4.png) |
( 32) |
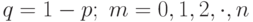 . Очевидно, что
. Очевидно, что![\[ F(x)=\left\{\begin{array}{ccc}{0, \ \ \ \ \ \ n \leqslant 0}\\{\sum\limits_{m=0}^n p_{m,n}, 0 <m \leqslant n}\\{1, m>n}, \\ \end{array}\right} \]](/sites/default/files/tex_cache/8e66d4637a8f6fb71586df25c3e09697.png) |
( 33) |
![\[ M_{X}=np, \]](/sites/default/files/tex_cache/e7012558b5ebeaedd07141ad8e7beaac.png)
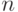 событиях искомое событие состоится хотя бы один раз.
событиях искомое событие состоится хотя бы один раз.Теорема Муавра-Лапласа
Эту теорему используют для вычисления 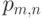 вместо формулы (31), если достаточно большое число. Эта теорема относится к предельным теоремам, которые используются вместо основных, если речь идет о большом количестве испытаний. В Математической статистике подобных теорем достаточно много.
вместо формулы (31), если достаточно большое число. Эта теорема относится к предельным теоремам, которые используются вместо основных, если речь идет о большом количестве испытаний. В Математической статистике подобных теорем достаточно много.
Теорема. Если вероятность наступления события 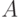 в
в 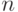 независимых испытаниях есть величина постоянная и отличная от нуля, то вероятность того, что в
независимых испытаниях есть величина постоянная и отличная от нуля, то вероятность того, что в 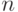 испытаниях событие
испытаниях событие 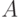 насупит
насупит 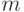 раз равна
раз равна
![\[ p_{m,n}=\frac 1 {\sqrt {mpq}} \cdot f(t), \]](/sites/default/files/tex_cache/e1006000c9c06fc3e5dc2f57fa37cb7f.png) |
( 34) |
![\[ f(t)=\frac 1 {\sqrt {2\pi}} e^{- \frac {t^2} 2}, \ t=\frac {m-np} {\sqrt {npq}} \]](/sites/default/files/tex_cache/9e41253f8ee5ce032ddc1f69accf5d6e.png) |
( 35) |
Пример 4. Вероятность того, что на морском берегу среди камней найдется гладкий (обкатанный) равна  . За 3 часа прогулки по берегу Некто собрал 280 разных по форме камушков. Найти вероятность того, что 20 камней из собранных будут не гладкими (не обкатанными прибоем).
. За 3 часа прогулки по берегу Некто собрал 280 разных по форме камушков. Найти вероятность того, что 20 камней из собранных будут не гладкими (не обкатанными прибоем).
Решение. Так как в задаче речь идет о большом количестве образцов ( ), то здесь следует воспользоваться теоремой Маувра-Лапласа (34) – (35). Для этого выполним некоторые предварительные расчеты по формулам (35).
![\[ t=\frac {m-np} {\sqrt {npq}}=\frac {20-280 \cdot \frac 19} {\sqrt {280 \cdot \frac 1 9 \cdot \frac 8 9}} = -2,11 \]](/sites/default/files/tex_cache/105a173313ade11baaa5d7eed1ef863e.png)
 принимаем
принимаем  , тогда
, тогда  . По специальным таблицам определяем значение функции распределения
. По специальным таблицам определяем значение функции распределения![\[ f(-t)=f(t)=0,0431 \]](/sites/default/files/tex_cache/99788e77ba81fdf1cf1beb0f74ffa60e.png)
![\[ p_{20,280}=\frac {0,0431} {\sqrt {280 \cdot \frac 1 9 \cdot \frac 8 9}} \approx 0,0082.\]](/sites/default/files/tex_cache/746fa815aaa12a5ee416bd085f422e74.png)