НОУ ИНТУИТ | Введение в математическое моделирование. Лекция 9: Компьютерное моделирование и решение линейных и нелинейных многомерных систем

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Донецкий национальный технический университет

Опубликован: 15.03.2007 | Доступ: свободный | Студентов: 6085 / 2196 | Оценка: 4.11 / 3.78 | Длительность: 12:32:00

Темы: Алгоритмы и дискретные структуры, Математика

Специальности: Математик

|

Вам нравится? Нравится 68 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

На третьем шаге прямого хода (к=3) из системы (9.7) находим x₃.

$a_{33}^{(2)}$ - ведущий элемент системы (9.7).

Если $a_{33}^{(2)} \neq 0$ , то из первого уравнения системы (9.7) имеем:

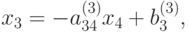$x_3= -a_{34}^{(3)}x_4 + b_3^{(3)},$

( 9.8)

где

$a_{3j}^{(3)} = a_{3j}^{(2)}/ a_{33}^{(2)},\\ b_3^{(3)} = b_3^{(2)}/ a_{33}^{(2)},\\ j=4=\overline{(k+1),n}$

Подставив выражение (9.8) для x₃ во второе уравнение системы (9.7) получим:

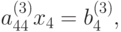$a_{44}^{(3)}x_4 = b_4^{(3)},$

( 9.9)

где

$a_{ij}^{(3)} = a_{ij}^{(2)} - a_{i3}^{(2)} \cdot a_{3j}^{(3)},\\ b_i^{(3)} = b_i^{(2)} - a_{i3}^{(2)} \cdot a_{3j}^{(3)},\\ i=\overline{(k+1),n}; j=\overline{(k+1),n}.$

На последнем шаге прямого хода, если $a_{44}^{(3)} \neq 0,$ то из уравнения (9.9) имеем:

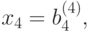$x_4 = b_4^{(4)},$

( 9.10)

где

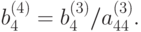$b_4^{(4)} = b_4^{(3)}/ a_{44}^{(3)}.$

( 9.11)

В результате выполнения всех шагов прямого хода исходная система (9.1) приводится к системе треугольного вида, полученной объединением уравнений (9.4), (9.6), (9.8), (9.10):

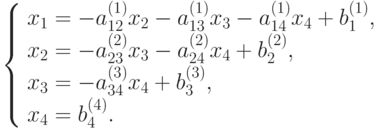$\left\{ \begin{array}{l} x_1= -a_{12}^{(1)}x_2 - a_{13}^{(1)}x_3 - a_{14}^{(1)}x_4 + b_1^{(1)},\\ x_2= -a_{23}^{(2)}x_3 - a_{24}^{(2)}x_4 + b_2^{(2)},\\ x_3= -a_{34}^{(3)}x_4 + b_3^{(3)},\\ x_4= b_4^{(4)}. \end{array} \right.$

( 9.12)

При построении алгоритма прямого хода вычисление организуем в цикле по шагам, т.е. $k=\overline{1,(n-1)}$ .

Последний n-й шаг прямого хода выведем из цикла т.к. здесь реализуется только одно вычисление

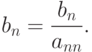$b_n=\frac{b_n}{a_{nn}}.$

( 9.13)

В процессе выполнения всех шагов прямого хода все преобразования коэффициентов и свободных членов проводим по полученным ранее рекуррентным формулам:

$b_k^{(k)}= b_k^{(k-1)}/a_k,k^{(k-1)},\\ b_i^{(k)}= b_i^{(k-1)}/a_i,k^{(k-1)} \cdot b_k^{(k)},\\ a_{k,j^{(k)}}= a_{k,j^{(k-1)}}/a_{k,k^{(k-1)}},\\ a_{i,j^{(k)}}= a_{i,j^{(k-1)}}-a_{i,k^{(k-1)}} \cdot a_{k,j^{(k)}},$

( 9.14)

где

$k=\overline{1,(n-1)}$ – номер шага прямого хода,

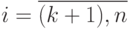$i=\overline{(k+1),n}$ - номер уравнения систем (9.5), (9.7)

$j=\overline{(k+1),n}$

В процессе обратного хода из системы (9.12) неизвестные находятся в обратном порядке. Значение корня х₄ находят из последнего уравнения системы (9.12). Далее х₄ используется для отыскания корня х₃ из 3-го уравнения, далее х₃ и х₄ используются отыскания х₂ из 2-го уравнения системы (9.12), и, наконец, х₂, х₃ и х₄ используются для отыскания х₁ из 1-го уравнения системы (9.12).

Все вычисления обратного хода проводим в цикле по i, где

$i=\overline{(n-1)},1$ по рекуррентным формулам:

$b_i={b_i – x_j \cdot a_{ij}} , \\ \overline i=(n-1),\overline {1,j}=(i+1),n$

x_i= b_i.

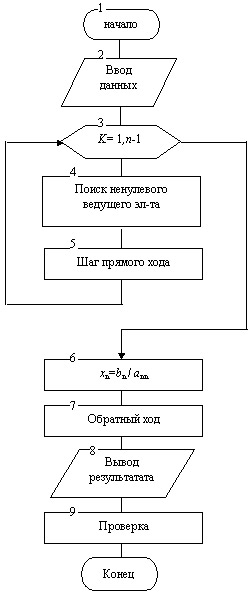
Рассмотренный выше простейший вариант метода Гаусса, называемый схемой единственного деления, обладает следующим недостатком: если ведущий элемент a_kk какой-либо строки окажется равным нулю, то этот метод формально непригоден, хотя система может иметь единственное решение. Из этих соображений в схеме алгоритма добавлен поиск ненулевого ведущего элемента.

На рисунке 9.1 представлена укрупнённая схема алгоритма (блок-схема) метода Гаусса. На рисунках 9.2 - 9.6 представлены алгоритмы отдельных блоков метода.

Рис. 9.1. Укрупнённая схема алгоритма (блок-схема) метода Гаусса

Дальше >>

Авторизоваться

Введение в математическое моделирование

Компьютерное моделирование и решение линейных и нелинейных многомерных систем

Вопросы и ответы