|
В уравнениях движения кривошипно-шатунного механизма вместо обозначения радиуса кривошипа "r" ошибочно записан символ "?" (гамма). P.S. Может быть это слишком очевидно, но не упомянуто, что угол поворота кривошипа ? считается малым. |
Компьютерное моделирование и вычислительный эксперимент. Решение математических моделей
Компьютерное моделирование как новый метод научных исследований основывается на:
- построении математических моделей для описания изучаемых процессов;
- использовании новейших вычислительных машин, обладающих высоким быстродействием (миллионы операций в секунду) и способных вести диалог с человеком.
Суть компьютерного моделирования состоит в следующем: на основе математической модели с помощью ЭВМ проводится серия вычислительных экспериментов, т.е. исследуются свойства объектов или процессов, находятся их оптимальные параметры и режимы работы, уточняется модель. Например, располагая уравнением, описывающим протекание того или иного процесса, можно изменяя его коэффициенты, начальные и граничные условия, исследовать, как при этом будет вести себя объект. Более того, можно спрогнозировать поведение объекта в различных условиях.
Вычислительный эксперимент позволяет заменить дорогостоящий натурный эксперимент расчетами на ЭВМ. Он позволяет в короткие сроки и без значительных материальных затрат осуществить исследование большого числа вариантов проектируемого объекта или процесса для различных режимов его эксплуатации, что значительно сокращает сроки разработки сложных систем и их внедрение в производство.
Компьютерное моделирование и вычислительный эксперимент как новый метод научного исследования заставляет совершенствовать математический аппарат, используемый при построении математических моделей, позволяет, используя математические методы, уточнять, усложнять математические модели. Наиболее перспективным для проведения вычислительного эксперимента является его использование для решения крупных научно-технических и социально-экономических проблем современности (проектирование реакторов для атомных электростанций, проектирование плотин и гидроэлектростанций, магнитогидродинамических преобразователей энергии, и в области экономики – составление сбалансированного плана для отрасли, региона, для страны и др.).
В некоторых процессах, где натурный эксперимент опасен для жизни и здоровья людей, вычислительный эксперимент является единственно возможным (термоядерный синтез, освоение космического пространства, проектирование и исследование химических и других производств).
Для проверки адекватности математической модели и реального объекта, процесса или системы результаты исследований на ЭВМ сравниваются с результатами эксперимента на опытном натурном образце. Результаты проверки используются для корректировки математической модели или решается вопрос о применимости построенной математической модели к проектированию либо исследованию заданных объектов, процессов или систем.
В заключение подчеркнем еще раз, что компьютерное моделирование и вычислительный эксперимент позволяют свести исследование "нематематического" объекта к решению математической задачи. Этим самым открывается возможность использования для его изучения хорошо разработанного математического аппарата в сочетании с мощной вычислительной техникой. На этом основано применение математики и ЭВМ для познания законов реального мира и их использования на практике.
В задачах проектирования или исследования поведения реальных объектов, процессов или систем математические модели, как правило, нелинейны, т.к. они должны отражать реальные физические нелинейные процессы, протекающие в них. При этом параметры (переменные) этих процессов связаны между собой физическими нелинейными законами. Поэтому в задачах проектирования или исследования поведения реальных объектов, процессов или систем чаще всего используются математические модели типа ДНА.
Согласно классификации приведенной в "лекции 1" :
Д – модель детерминированная, отсутствует (точнее не учитывается) влияние случайных процессов.
Н – модель непрерывная, информация и параметры непрерывны.
А – модель аналитическая, функционирование модели описывается в виде уравнений (линейных, нелинейных, систем уравнений, дифференциальных и интегральных уравнений).
Итак, мы построили математическую модель рассматриваемого объекта, процесса или системы, т.е. представили прикладную задачу как математическую. После этого наступает второй этап решения прикладной задачи – поиск или разработка метода решения сформулированной математической задачи. Метод должен быть удобным для его реализации на ЭВМ, обеспечивать необходимое качество решения.
Все методы решения математических задач можно разделить на 2 группы:
- точные методы решения задач;
- численные методы решения задач.
В точных методах решения математических задач ответ удается получить в виде формул.
Например, вычисление корней квадратного уравнения:
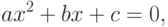
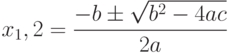
или, например, вычисление производных функций:
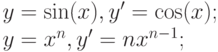
или вычисление определенного интеграла:
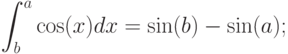
Однако, подставляя числа в формулу в виде конечных десятичных дробей, мы все равно получаем приближенные значения результата.
Для большинства задач, встречающихся на практике, точные методы решения или неизвестны, или дают очень громоздкие формулы. Однако, они не всегда являются необходимыми. Прикладную задачу можно считать практически решенной, если мы сумеем ее решить с нужной степенью точности.
Для решения таких задач разработаны численные методы, в которых решение сложных математических задач сводится к последовательному выполнению большого числа простых арифметических операций. Непосредственная разработка численных методов относится к вычислительной математике.
Примером численного метода является метод прямоугольников для приближенного интегрирования, не требующий вычисления первообразной для подынтегральной функции. Вместо интеграла вычисляется конечная квадратурная сумма:
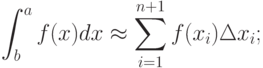
где
x1=a – нижний предел интегрирования;
xn+1=b – верхний предел интегрирования;
n – число отрезков, на которые разбит интервал интегрирования (a,b) ;
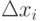 – длина элементарного отрезка;
– длина элементарного отрезка;
f(xi) – значение подынтегральной функции на концах элементарных отрезков интегрирования.
Чем больше число отрезков n, на которые разбит интервал интегрирования, тем ближе приближенное решение к истинному, т.е. тем точнее результат.
Таким образом, в прикладных задачах и при применении точных методов решения, и при применении численных методов решения результаты вычислений носят приближенный характер. Важно только добиться того, чтобы ошибки укладывались в рамки требуемой точности.
Численные методы решения математических задач известны давно, еще до появления ЭВМ, но ими пользовались редко и только в сравнительно простых случаях в силу чрезвычайной трудоемкости вычислений. Широкое применение численных методов стало возможным благодаря ЭВМ.
