Предсказание финансовых временных рядов
Использование комитетов сетей
Из-за случайности в выборе начальных значений синаптических весов, предсказания сетей, обученных на одной и той же выборке, будут, вообще говоря, разниться. Этот недостаток (элемент неопределенности) можно превратить в достоинство, организовав комитет нейро-экспертов, состоящий из различных нейросетей. Разброс в предсказаниях экспертов даст представление о степени уверенности этих предсказаний, что можно использовать для правильного выбора стратегии игры.
Легко показать, что среднее значений комитета должно давать лучшие предсказания, чем средний эксперт из этого же комитета.
Пусть ошибка  -ого эксперта для значения входа
-ого эксперта для значения входа  равна
равна 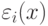 . Средняя ошибка комитета всегда меньше среднеквадратичной ошибки отдельных
экспертов в силу неравенства Коши:
. Средняя ошибка комитета всегда меньше среднеквадратичной ошибки отдельных
экспертов в силу неравенства Коши:
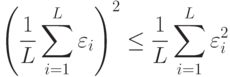
Причем, снижение ошибки может быть довольно заметным. Так, если ошибки отдельных экспертов не коррелируют друг с другом, т. е. 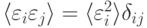 , то среднеквадратичная ошибка комитета из
, то среднеквадратичная ошибка комитета из  экспертов в
экспертов в 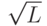 раз меньше, чем средняя индивидуальная ошибка одного эксперта!
раз меньше, чем средняя индивидуальная ошибка одного эксперта!
Поэтому, в предсказаниях всегда лучше опираться на средние значения всего комитета. Иллюстрацией этого факта служит рисунок 8.12.
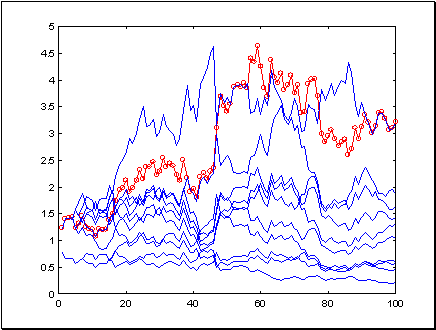
Рис. 8.12. Норма прибыли на последних 100 значениях ряда sp500 при предсказании комитетом из 10 сетей. Выигрыш комитета (кружки) выше, чем выигрыш среднего эксперта. Счет угаданных знаков для комитета 59:41
Как видно из приведенного выше рисунка, в данном случае выигрыш комитета даже выше, чем выигрыш каждого из экспертов. Таким образом, метод комитетов может существенно повысить качество прогнозирования. Обратите внимание на абсолютное значение нормы прибыли: капитал комитета возрос в 3.25 раза при 100 вхождениях в рынок (Естественно, эта норма будет ниже при учете транзакционных издержек).
Предсказания получены при обучении сети на 30 последовательных экспоненциальных скользящих средних (EMA1 … EMA30) ряда приращений индекса. Предсказывался знак приращения на следующем шаге.
В этом эксперименте ставка была зафиксирована на уровне 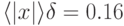 , близком к оптимальному при данной точности предсказаний (59 угаданных
знаков против 41 ошибки) т.е.
, близком к оптимальному при данной точности предсказаний (59 угаданных
знаков против 41 ошибки) т.е. 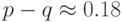 . На следующем же рисунке приведены результаты более рискованной игры по тем же предсказаниям, а именно
- с
. На следующем же рисунке приведены результаты более рискованной игры по тем же предсказаниям, а именно
- с 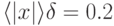 .
.
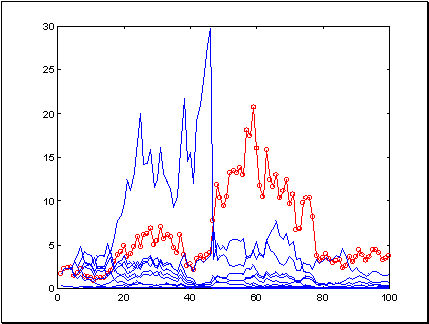
Рис. 8.13. Норма прибыли на последних 100 значениях ряда sp500 при тех же предсказаниях комитета из 10 сетей, но по более рискованной стратегии
Выигрыш комитета в целом остался на прежнем уровне (чуть увеличился), поскольку данное значение риска так же близко к оптимуму, как и предыдущее. Однако, для большинства сетей, предсказания которых хуже, чем у комитета в целом, такие ставки оказались слишком рискованными, что привело к практически полному их разорению.
Приведенные выше примеры показывают как важно уметь правильно оценить качество предсказания и как можно использовать эту оценку для увеличения прибыльности от одних и тех же предсказаний.
Можно пойти еще дальше и вместо среднего использовать взвешенное мнение сетей-экспертов. Веса выбираются адаптивно максимизируя предсказательную способность комитета на обучающей выборке. В итоге, хуже обученные сети из комитета вносят меньший вклад и не портят предсказания.
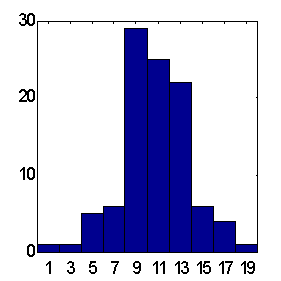
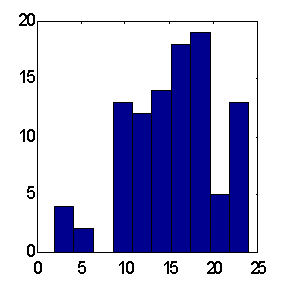
Возможности этого пути иллюстрирует приведенное ниже сравнение предсказаний двух типов комитетов из 25 экспертов (см. рисунки 8.14,8.15). Предсказания проводились по одной и той же схеме: в качестве входов использовались экспоненциальные скользящие средние приращений ряда с периодами равными первым 10 числам Фибоначчи. По результатам 100 экспериментов взвешенное предсказание дает в среднем превышение правильно угаданных знаков над ошибочным равное примерно 15, тогда как среднее - около 12. Заметим, что общее число повышений курса над понижением за указанный период как раз равно 12. Следовательно, учет общей тенденции к повышению в виде тривиального постоянного предсказания знака "+" дает такой же результат для процента угаданных знаков, что и взвешенное мнение 25 экспертов.