Нейросетевая оптимизация
В Смеральдине, городе на воде, сеть каналов накладывается и пересекается с сетью улиц. Чтобы добраться от одного места к другому, всегда можно выбрать между сухопутной дорогой и лодкой, но поскольку в Смеральдине самый короткий путь пролегает не по прямой линии, а по зигзагообразной, - Итало Кальвино, "Незримые города"
Сети минимизирующие энергию, рассмотренные в предыдущей лекции, при релаксации к одному из своих стационарных состояний решают, по существу, оптимизационную задачу - поиск минимума определенной функции своего состояния - энергии. Следовательно, и ассоциативную выборку информации, и выявление прототипов можно сформулировать как частный случай задачи оптимизации. В целом же, оптимизационные задачи представляют собой широкий класс задач, часто встречающихся на практике, в частности, в экономике и бизнесе. В этой лекции мы покажем как нейросети можно приспособить к решению таких задач на примере очень важного класса задач комбинаторной оптимизации. Такие задачи, кроме прочего, позволят нам познакомиться с новыми методами оптимизации, отличающимися от градиентных методов, лежащих в основе обучения методом backpropagation.
Комбинаторная оптимизация и задача коммивояжера
В задачах комбинаторной оптимизации требуется найти наилучшее из конечного, но обычно очень большого числа возможных решений. Если
задача характеризуется характерным числом элементов (размерностью задачи), то типичное число возможных решений, из которых предстоит
сделать выбор, растет экспоненциально - как 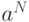 или еще скорее - как
или еще скорее - как  ! (напомним, что согласно известной формуле Стирлинга
! (напомним, что согласно известной формуле Стирлинга 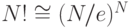 для
достаточно больших
для
достаточно больших  ).
).
Это свойство делает простой метод перебора всех вариантов, в принципе гарантирующий решение при конечном числе альтернатив, чрезвычайно неэффективным, т.к. такое решение требует экспоненциально большого времени. Эффективными же признаются решения, гарантирующие получение ответа за полиномиальное время, растущее как полином с ростом размерности задачи, т.е. как N1Практически при больших размерностях осуществимы все-таки не всякие полиномиальные решения, а лишь полиномы низших степеней.
Задачи, допускающие гарантированное нахождение оптимума целевой функции за полиномиальное время, образуют класс  . Этот класс
является подклассом более обширного класса
. Этот класс
является подклассом более обширного класса 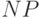 задач, в которых за полиномиальное время можно всего лишь оценить значение целевой функции
для конкретной конфигурации, что, естественно, гораздо проще, чем выбрать наилучшую из всех конфигураций. До сих пор в точности не
известно, совпадают ли эти два класса, или нет. Эта проблема,
задач, в которых за полиномиальное время можно всего лишь оценить значение целевой функции
для конкретной конфигурации, что, естественно, гораздо проще, чем выбрать наилучшую из всех конфигураций. До сих пор в точности не
известно, совпадают ли эти два класса, или нет. Эта проблема,  , о которую сломано уже немало математических копий. Если бы эти классы
совпадали, для любой задачи комбинаторной оптимизации, точное решение можно было бы гарантированно найти за полиномиальное время. В такой
"подарок судьбы" никто не верит, и практически разрешимыми считаются задачи, допускающие полиномиальное решение хотя бы
для типичных (а не наихудших) случаев. Такова, например, общая задача линейного программирования.
, о которую сломано уже немало математических копий. Если бы эти классы
совпадали, для любой задачи комбинаторной оптимизации, точное решение можно было бы гарантированно найти за полиномиальное время. В такой
"подарок судьбы" никто не верит, и практически разрешимыми считаются задачи, допускающие полиномиальное решение хотя бы
для типичных (а не наихудших) случаев. Такова, например, общая задача линейного программирования.
Для более трудных задач достаточно было бы и более слабого условия - нахождения субоптимальных решений, локальных минимумов целевой функции, не слишком сильно отличающихся от абсолютного минимума. Нейросетевые решения как раз и представляют собой параллельные алгоритмы, быстро находящие субоптимальные решения оптимизационных задач, минимизируя целевую функцию в процессе своего функционирования или обучения.
Самые трудные задачи класса 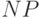 называют
называют 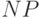 -полными. Это название объясняется тем, что если бы удалось доказать, что существует
полиномиальное решение такой задачи, то такое решение существовало бы и для любой другой задачи класса
-полными. Это название объясняется тем, что если бы удалось доказать, что существует
полиномиальное решение такой задачи, то такое решение существовало бы и для любой другой задачи класса 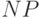 , т.е. классы
, т.е. классы  и
и 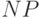 совпадали
бы. Поскольку, как уже говорилось, такой сценарий крайне маловероятен, именно для таких проблем наиболее важен поиск субоптимальных
решений.
совпадали
бы. Поскольку, как уже говорилось, такой сценарий крайне маловероятен, именно для таких проблем наиболее важен поиск субоптимальных
решений.
Все 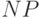 -полные задачи одинаково сложны (поскольку все они сводятся друг к другу за полиномиальное время), и методы решения любой
из них можно применять также и к другим задачам комбинаторной оптимизации. Поэтому нам в этой лекции достаточно сосредоточиться на
одной такой задаче. Исторически наиболее исследованной и популярной задачей такого рода (своего рода "мушкой дрозофилой"
комбинаторной оптимизации), которая используется для сравнения различных алгоритмов, стала задача коммивояжера.
-полные задачи одинаково сложны (поскольку все они сводятся друг к другу за полиномиальное время), и методы решения любой
из них можно применять также и к другим задачам комбинаторной оптимизации. Поэтому нам в этой лекции достаточно сосредоточиться на
одной такой задаче. Исторически наиболее исследованной и популярной задачей такого рода (своего рода "мушкой дрозофилой"
комбинаторной оптимизации), которая используется для сравнения различных алгоритмов, стала задача коммивояжера.
В классической постановке, коммивояжер должен объехать  городов по замкнутому маршруту, посетив каждый из них лишь однажды,
таким образом, чтобы полная длина его маршрута была минимальной. Если решать задачу коммивояжера "в лоб" - перебором всех
замкнутых путей, связывающих
городов по замкнутому маршруту, посетив каждый из них лишь однажды,
таким образом, чтобы полная длина его маршрута была минимальной. Если решать задачу коммивояжера "в лоб" - перебором всех
замкнутых путей, связывающих  городов, то придется проверить все
городов, то придется проверить все 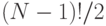 возможных маршрутов. Будучи
возможных маршрутов. Будучи 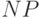 -полной, задача коммивояжера не имеет
практически реализуемого точного решения. На примере этой задачи мы ниже и рассмотрим различные методы ее приближенного решения с
помощью нейросетей.
-полной, задача коммивояжера не имеет
практически реализуемого точного решения. На примере этой задачи мы ниже и рассмотрим различные методы ее приближенного решения с
помощью нейросетей.
