Нейросетевая оптимизация
Оптимизация с помощью сети Кохонена.
Успех применения метода эластичной сети для решении задачи коммивояжера был оценен Фаватой и Уолкером, понявшими, что в нем, по сути, используется отображение двумерного распределения городов на одномерного кольцевого маршрута (Favata & Walker, 1991). Поскольку в наиболее общем виде такой подход был сформулирован Кохоненом, то использование его самоорганизующихся карт для оптимизации оказалось вполне естественным. Сеть Кохонена позволяет обеспечить выполнение условия, которому должен удовлетворять хороший маршрут в задаче коммивояжера: близкие города на плоскости должны быть отображены на близкие в одномерном маршруте.
Алгоритм решения задачи следует из оригинальной схемы Кохонена, в которую вносятся лишь небольшие изменения. Используется сеть,
состоящая из двух одномерных слоев нейронов (т.е. содержащая лишь один слой синаптических весов). Входной слой состоит из трех нейронов,
а выходной - из N (по числу городов). Каждый нейрон входного слоя связан с каждым выходным нейроном. Все связи вначале инициируются
случайными значениями. Для каждого города входной 3-мерный вектор формируется из двух его координат на плоскости, а третья компонента
вектора представляет из себя нормирующий параметр, вычисляемый так, чтобы все входные вектора имели одинаковую Евклидову длину и
никакие два вектора не были бы коллинеарны. Это эквивалентно рассмотрению двумерных координат городов, как проекций трехмерных
векторов, лежащих на сфере. Обозначим через  3-мерный вектор синаптических связей, связывающих
3-мерный вектор синаптических связей, связывающих  -й выходной нейрон с входными
нейронами. Если
-й выходной нейрон с входными
нейронами. Если 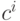 - трехмерный входной вектор, определяющий i -й город, то активация j-го выходного нейрона при
подаче
- трехмерный входной вектор, определяющий i -й город, то активация j-го выходного нейрона при
подаче 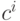 на вход определяется скалярным произведением
на вход определяется скалярным произведением 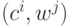 . Выходной нейрон, для которого это произведение максимально,
называется образом города.
. Выходной нейрон, для которого это произведение максимально,
называется образом города.
Алгоритм формирования маршрута формулируется следующим образом. Выбираются значения для параметра усиления  и радиуса
взаимодействия r. Следующий цикл выполняется вплоть до выполнения условия
и радиуса
взаимодействия r. Следующий цикл выполняется вплоть до выполнения условия  .
.
- Выбирается случайный город
 .
. - Определяется номер образа города в выходном слое -
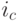 .
. - Векторы связей
 , соединяющих нейрон
, соединяющих нейрон 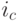 , и всех его
, и всех его 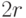 близлежащих соседей справа и слева:
близлежащих соседей справа и слева: 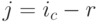 ,
, 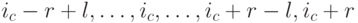 модифицируются следующим образом:, где
модифицируются следующим образом:, где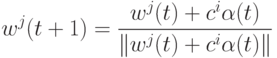
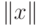 - Евклидова норма вектора
- Евклидова норма вектора  . Для устранения концевых эффектов слой выходных нейронов считается кольцевым, так что N-й нейрон
примыкает к первому.
. Для устранения концевых эффектов слой выходных нейронов считается кольцевым, так что N-й нейрон
примыкает к первому. - Радиус взаимодействия постепенно уменьшается согласно некоторому правилу (например, вначале можно положить
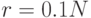 , затем за первые
10% циклов снизить его до значения 1, которое далее поддерживается постоянным).
, затем за первые
10% циклов снизить его до значения 1, которое далее поддерживается постоянным). - Параметр усиления
 постепенно снижается на небольшую величину ( например, в экспериментах Фавата и Уолкера он линейно уменьшался
до нуля).
постепенно снижается на небольшую величину ( например, в экспериментах Фавата и Уолкера он линейно уменьшался
до нуля).
Конкретный вид законов изменения радиуса взаимодействия и параметра усиления, как правило, не имеет большого значения.
После завершения процесса обучения, положение города в маршруте определится положением его образа в кольцевом выходном слое. Иногда случается, что два или большее число городов отображаются на один и тот же выходной нейрон. Подобная ситуация может интерпретироваться так, что локальное упорядочивание этих городов не имеет значения и требует только локальной оптимизации части маршрута. При нескольких десятках городов такая оптимизация может скорректировать его длину на величину до 25%. Для сотен городов она, как правило, не улучшает результат и поэтому не используется.
Эксперименты Фаваты и Уолкера, проведенные для задачи коммивояжера с 30 городами дали лучшие результаты, чем полученные с помощью сети Хопфилда (см. таблицу).
| сеть Хопфилда | сеть Кохонена | |
|---|---|---|
| Длина маршрута | <7 | <5.73 |
| Средняя длина маршрута | >6 | 4.77 |
| Наименьшая длина маршрута | 5.07 | 4.26 |
Однако для большего числа городов сеть Кохонена все же в среднем дает более длинные маршруты, чем метод имитации отжига
(примерно на 5%). При практическом применении нейросетевых подходов к решению задач оптимизации, однако, главное значение имеет не
столько близость решения к глобальному оптимуму, сколько эффективность его получения. В этом смысле сеть Кохонена значительно
эффективнее имитации отжига. Однако, и ее использование, как и в случае использования других лучших методов оптимизации, требует
вычислительных затрат, растущих не медленне, чем 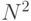 . Ниже мы опишем нейросетевой подход, в котором они растут линейно с
размерностью задачи.
. Ниже мы опишем нейросетевой подход, в котором они растут линейно с
размерностью задачи.
