Нейросетевая оптимизация
Растущие нейронные сети
Эффективное практическое применение нейронных сетей для оптимизации возможно, если вычислительные затраты у соответствующей модели
не слишком быстро растут с ростом размерности задачи. Так, для задачи коммивояжера затраты при эмуляции сети Хопфилда на
последовательном компьютере растут как 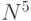 , т.к. каждый из
, т.к. каждый из 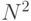 нейронов имеет порядка
нейронов имеет порядка 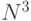 синаптических весов3Параллельный же аналоговый вариант сети Хопфилда находит решение за конечное число шагов, практически не зависящее от
синаптических весов3Параллельный же аналоговый вариант сети Хопфилда находит решение за конечное число шагов, практически не зависящее от  .
Эвристический подход Лина и
Кернигана масштабирует вычислительные затраты как
.
Эвристический подход Лина и
Кернигана масштабирует вычислительные затраты как 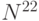 . Фритцке и Вильке предложили нейросетевую систему очень близкую к сети Кохонена,
для которой затраты даже при ее эмуляции на последовательном компьютере растут лишь линейно с размерностью задачи (Fritzke &
Wilke, 1991).
. Фритцке и Вильке предложили нейросетевую систему очень близкую к сети Кохонена,
для которой затраты даже при ее эмуляции на последовательном компьютере растут лишь линейно с размерностью задачи (Fritzke &
Wilke, 1991).
Предложенная ими модель относится к классу растущих нейронных сетей. Такие сети по-своему решают задачу адаптации своей структуры к требованиям решаемой задачи. Вспомним многослойные персептроны, для которых количества скрытых слоев и нейронов в них часто выбираются методом проб и ошибок. Как уже отмечалось в связи с этим, имеются два подхода к адаптивному выбору архитектуры нейросетей. В первом подходе заведомо избыточная нейросеть прореживается до нужной степени сложности. Растущие сети, напротив, стартуют с очень простых и небольших структур, которые разрастаются и усложняются по мере необходимости.
Фритцке и Вильке разработали целый класс самоорганизующихся (и обучаемых с учителем) сетей с изменяющейся структурой, такие как Растущие Клеточные Структуры, Растущий Нейронный Газ и Растущие Сетки. Первые и были использованы ими для решения задачи коммивояжера (и других задач комбинаторной оптимизации).
Растущая клеточная структура для задачи коммивояжера представляет из себя вначале кольцо из трех ячеек нейронов. Каждый
нейрон характеризуется двумерным вектором 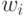 , определяющим его положение на плоскости. Каждому нейрону в кольце приписывается
также своя величина погрешности
, определяющим его положение на плоскости. Каждому нейрону в кольце приписывается
также своя величина погрешности 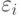 , которая вначале полагается равной нулю. Дальнейшая последовательность действий включает две
следующие основные элементарные операции: смещение и добавление нового нейрона.
Смещение (см. рисунок 6.2)
, которая вначале полагается равной нулю. Дальнейшая последовательность действий включает две
следующие основные элементарные операции: смещение и добавление нового нейрона.
Смещение (см. рисунок 6.2)
- выбирается случайный город

- определяется нейрон-победитель
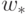 , ближайший к этому городу
, ближайший к этому городу - положение нейрона
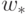 и его двух ближайших в кольце соседей смещается в сторону города
и его двух ближайших в кольце соседей смещается в сторону города  на определенную долю расстояния до него.
на определенную долю расстояния до него.
Эти операции очень близки к используемым в модели Кохонена. Различие состоит в том, что в последней радиус, в котором определяется соседство и параметр адаптации уменьшаются со временем.
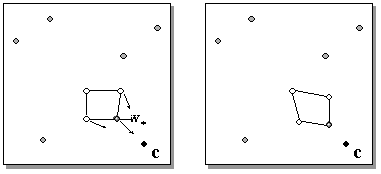
Рис. 6.2. Процедура смещения перемещает нейрон-победитель и его ближайших соседей в сторону случайно выбранного города
Добавление нового нейрона.
Со временем после нескольких циклов смещений накапливается информация, на основании которой принимается решение о месте, в котором
должен быть добавлен новый нейрон. Каждый раз, когда для случайно выбранного города  определяется ближайший к нему нейрон
определяется ближайший к нему нейрон 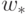 , локальная
ошибка для последнего
, локальная
ошибка для последнего 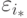 получает приращение
получает приращение  . Большое значение этой ошибки служит указанием на то, что соответствующий нейрон лежит
в области, где отношение (число нейронов)/(число городов) невелико. Именно в таких областях следует добавлять новые нейроны,
поскольку для получения правильного осмысленного маршрута около каждого города должен находиться свой ближайший нейрон. Маршрут и
определяется путем перехода вдоль кольца к нейрону, являющимся ближайшим к некоторому городу. Алгоритм поиска оптимального маршрута,
использующий две описанные операции, формулируется следующим образом
. Большое значение этой ошибки служит указанием на то, что соответствующий нейрон лежит
в области, где отношение (число нейронов)/(число городов) невелико. Именно в таких областях следует добавлять новые нейроны,
поскольку для получения правильного осмысленного маршрута около каждого города должен находиться свой ближайший нейрон. Маршрут и
определяется путем перехода вдоль кольца к нейрону, являющимся ближайшим к некоторому городу. Алгоритм поиска оптимального маршрута,
использующий две описанные операции, формулируется следующим образом
- Инициализация: генерируется кольцевая структура, состоящая из трех нейронов, имеющих случайное положение на плоскости.
- Осуществляется фиксированное число
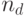 шагов распространения. На каждом шаге пересчитывается значение локальной ошибки
шагов распространения. На каждом шаге пересчитывается значение локальной ошибки 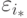 .
. - Определяется "наихудшее" звено в кольце, связывающее два нейрона
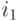 и
и 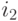 , для которых сумма
, для которых сумма  максимально. Новый нейрон
вставляется в середину звена связывающего нейроны
максимально. Новый нейрон
вставляется в середину звена связывающего нейроны 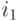 и
и 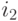 , и его ошибка инициализируется величиной
, и его ошибка инициализируется величиной 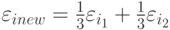 . В то же время значения ошибок для
нейронов
. В то же время значения ошибок для
нейронов 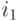 и
и 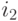 уменьшается таким образом, чтобы суммарная ошибка сохранилась:
уменьшается таким образом, чтобы суммарная ошибка сохранилась: 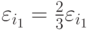 ,
, 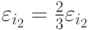
- Если для любых двух городов ближайшие к ним нейроны различны между собой, то маршрут найден. В противоположном случае возвращаемся к шагу 1.
Очевидно, что решение задачи может быть найдено не ранее того, как число нейронов в кольце достигнет числа городов  .
В действительности для его достижения требуется сеть с
.
В действительности для его достижения требуется сеть с  нейронами. Исходя из этого эмпирического наблюдения, согласно которому
число итераций имеет порядок
нейронами. Исходя из этого эмпирического наблюдения, согласно которому
число итераций имеет порядок 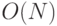 , можно оценить общую сложность алгоритма. На шаге 1 требуется инспекция всех нейронов для поиска
ближайшего к данному городу. Она производится
, можно оценить общую сложность алгоритма. На шаге 1 требуется инспекция всех нейронов для поиска
ближайшего к данному городу. Она производится  раз и, поскольку это число постоянно, полное число инспекций также имеет порядок
раз и, поскольку это число постоянно, полное число инспекций также имеет порядок 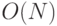 .
На шаге 2 необходимо проверить каждое звено цепи, чтобы найти то, которому соответствует максимальная суммарная ошибка концевых
нейронов. Поскольку число звеньев равно числу нейронов, то число действий опять имеет порядок
.
На шаге 2 необходимо проверить каждое звено цепи, чтобы найти то, которому соответствует максимальная суммарная ошибка концевых
нейронов. Поскольку число звеньев равно числу нейронов, то число действий опять имеет порядок 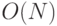 . На шаге 3 для каждого города необходимо
найти ближайший нейрон, что, как минимум, требует
. На шаге 3 для каждого города необходимо
найти ближайший нейрон, что, как минимум, требует 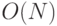 действий. Таким образом, так как шаги 1-3 требуют по меньшей мере
действий. Таким образом, так как шаги 1-3 требуют по меньшей мере 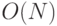 операций, а
цикл повторяется
операций, а
цикл повторяется 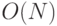 раз, то временная сложность алгоритма как минимум равна
раз, то временная сложность алгоритма как минимум равна  . Пространственная сложность
алгоритма составляет
. Пространственная сложность
алгоритма составляет 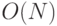 , так как необходимо резервировать память для
, так как необходимо резервировать память для  городов,
городов, 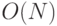 нейронов и некоторых локальных переменных.
нейронов и некоторых локальных переменных.
Для улучшения квадратичной временной сложности описанного алгоритма Фритцке и Вильке модифицировали шаги 1-3. Они учли, что
согласно численным экспериментам вначале кольцевая структура нейронов быстро распределяется по всей области размещения городов, и
затем с ростом числа нейронов изменения приобретают локальный характер. Такое поведение натолкнуло их на идею заменить глобальный
поиск нейрона-победителя на шаге 1 приближенной локальной процедурой. А именно: для каждого города запоминается тот нейрон, который
наиболее часто оказывался к нему ближайшим, и если город выбран вновь, то поиск ближайшего к нему нейрона ограничивается этим нейроном
и его ближайшими по кольцу соседями вплоть до порядка k. Поскольку k есть константа, то сложность поиска оказывается в этом случае 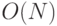 .
.
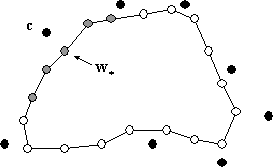
Рис. 6.3. Локальный поиск наилучшего нейрона: -предыдущий нейрон ; ближайшие его соседи вплоть до 2 порядка являются кандидатами в победители на следующем шаге
Для устранения на шаге 2 линейного поиска звена с максимальной ошибкой используется тот факт, что таким звеном является то, которое связывает нейроны, часто становящиеся победитями.
Третий шаг тоже можно модифицировать: если некоторый нейрон несколько раз оказывается ближайшим для данного города, значит для этого города структура кольца уже стабилизировалась и нейрон "приклеивается" к данному пункту маршрута. Это означает, что он совмещается со своим городом и больше уже не двигается. Город же удаляется из списка городов, разыгрываемых на шаге распределения. Когда этот список становится пустым процесс поиска маршрута заканчивается.
Таким образом, каждый шаг в цикле теперь требует постоянное число операций и временная сложность всего алгоритма становится
порядка 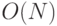 .
.
Описанный эффективный нейросетевой подход (FLEXMAP) был протестирован на разных распределениях городов числом до 200 и неизменно находил маршруты, отличающиеся не более чем на 9% от оптимального.
