Предсказание финансовых временных рядов
Измерение качества предсказаний
Хотя предсказание финансовых рядов и сводится к задаче аппроксимации многомерной функции, оно имеет свои особенности как при формировании входов, так и при выборе выходов нейросети. Первый аспект, касающийся входов, мы уже обсудили. Теперь коснемся особенностей выбора выходных переменных. Но прежде ответим на главный вопрос: как измерить качество финансовых предсказаний. Это поможет определить наилучшую стратегию обучения нейросети.
Связь предсказуемости с нормой прибыли
Особенностью предсказния финансовых временных рядов является стремление к получению максимальной прибыли, а не минимизации среднеквадратичного отклонения, как это принято в случае аппроксимации функций.
В простейшем случае ежедневной торговли прибыль зависит от верно угаданого знака изменения котировки. Поэтому нейросеть нужно ориентировать именно на точность угадывания знака, а не самого значения. Найдем как связана норма прибыли с точностью определения знака в простейшей постановке ежедневного вхождения в рынок ( рисунок 8.9).
Обозначим на момент  : полный капитал игрока
: полный капитал игрока 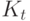 , относительное изменение котировки
, относительное изменение котировки  , а в качестве выхода сети возьмем степень ее
уверенности в знаке этого изменения
, а в качестве выхода сети возьмем степень ее
уверенности в знаке этого изменения ![y_t\in [-1,1]](/sites/default/files/tex_cache/12c6ff3812f8132ec253637ac3a054c7.png) . Такая сеть с выходной нелинейностью вида
. Такая сеть с выходной нелинейностью вида  обучается предсказывать знак изменения и выдает
прогноз знака с амплитудой пропорциональной его вероятности. Тогда возрастание капитала на шаге
обучается предсказывать знак изменения и выдает
прогноз знака с амплитудой пропорциональной его вероятности. Тогда возрастание капитала на шаге  запишется в виде:
запишется в виде:
![K_t=K_{t-1}[1+|x_t|\deltasgn(x_t,y_t)]](/sites/default/files/tex_cache/6654ad0424b162c7728d1b14f8bfce31.png)
 - доля капитала, "в игре". Выигрыш за все время игры:
- доля капитала, "в игре". Выигрыш за все время игры:![K_t=K_0 \exp\left(\sum_{k=1}^t\ln[1+x_k \deltasgn(y_k)]\right)](/sites/default/files/tex_cache/73ea7ab4a03f888bc158577bb1729b09.png)
 . Пусть в среднем игрок угадывает долю
. Пусть в среднем игрок угадывает долю  знаков и, соответственно,
ошибается с вероятностью
знаков и, соответственно,
ошибается с вероятностью  . Тогда логарифм нормы прибыли,
. Тогда логарифм нормы прибыли,
 и составит в среднем:
и составит в среднем:
Здесь мы ввели коэффициент  . Например, для Гауссова распределения
. Например, для Гауссова распределения  . Степень предсказуемости знака напрямую связана с
кросс-энтропией, которую можно оценить a priori методом box-counting. Для бинарного выхода (см.
рисунок 8.10):
. Степень предсказуемости знака напрямую связана с
кросс-энтропией, которую можно оценить a priori методом box-counting. Для бинарного выхода (см.
рисунок 8.10):

Рис. 8.10. Доля правильно угаданных направлений изменений ряда как функция кросс-энтропии знака выхода при известных входах
В итоге получаем следующую оценку нормы прибыли при заданной величине предсказуемости знака  , выраженной в битах:
, выраженной в битах:

То есть, для ряда с предсказуемостью  в принципе возможно удвоить капитал за
в принципе возможно удвоить капитал за  вхождений в рынок. Так, например, измеренная выше
предсказуемость временного ряда S&P500, равная
вхождений в рынок. Так, например, измеренная выше
предсказуемость временного ряда S&P500, равная  (см.
рисунок 8.8) предполагает удвоение капитала в среднем за
(см.
рисунок 8.8) предполагает удвоение капитала в среднем за  вхождений в рынок. Таким образом, даже
небольшая предсказуемость знака изменения котировок способна обеспечить весьма заметную норму прибыли.
вхождений в рынок. Таким образом, даже
небольшая предсказуемость знака изменения котировок способна обеспечить весьма заметную норму прибыли.
Подчеркнем, что оптимальная норма прибыли требует достаточно аккуратной игры, когда при каждом вхождении в рынок игрок рискует строго определенной долей капитала:

 - типичная при данной волатильности рынка
- типичная при данной волатильности рынка  величина выигрыша или проигрыша7Это отношение, в принципе, может быть не малым даже при очень маленькой волатильности - за счет механизмов залоговой торговли,
практикуемых на биржах
Как меньшие, так и большие значения ставок уменьшают прибыль. Причем, чересчур рискованная игра может привести к проигрышу при любой
предсказательной способности. Этот факт иллюстрирует
рисунок 8.11.
величина выигрыша или проигрыша7Это отношение, в принципе, может быть не малым даже при очень маленькой волатильности - за счет механизмов залоговой торговли,
практикуемых на биржах
Как меньшие, так и большие значения ставок уменьшают прибыль. Причем, чересчур рискованная игра может привести к проигрышу при любой
предсказательной способности. Этот факт иллюстрирует
рисунок 8.11.Поэтому приведенные выше оценки дают представление лишь о верхнем пределе нормы прибыли8Помимо явного пренебрежения комиссионными, вызывает сомнения само предположение о постоянном перевложении капитала. В более реалистичной игре на фиксированном капитале экспоненциальный рост сменяется линейным Более тщательный анализ с учетом влияния флуктуаций, выходит за рамки нашего изложения. Качественно понятно, однако, что выбор оптимального размера контрактов требует оценки точности предсказаний на каждом шаге.
Выбор функционала ошибки
Если принять, что целью предсказаний финансовых временных рядов является максимизация прибыли, логично настраивать нейросеть именно на этот конечный результат. Например, при игре по описанной выше схеме для обучения нейросети можно выбрать следующую функцию ошибки обучения, усредненную по всем примерам из обучающей выборки:
![E=-\langle\ln[1+x_t\delta_t sgn(y_t)]\rangle.](/sites/default/files/tex_cache/6efa28576fed8bb108f46cc871a75a90.png)
Здесь доля капитала в игре введена в качестве дополнительного выхода сети, настраиваемого в процессе обучения. При таком подходе,
первый нейрон,  с функцией активации
с функцией активации  даст вероятность возрастания или убывания курса, в то время
как второй выход сети
даст вероятность возрастания или убывания курса, в то время
как второй выход сети  даст рекомендованную долю капитала в игре на данном шаге.
даст рекомендованную долю капитала в игре на данном шаге.
Поскольку, однако, в соответствии с предыдущим анализом, эта доля должна быть пропорциональна степени уверености предсказания,
можно заменить два выхода сети - одним, положив  , и ограничиться оптимизацией всего одного глобального параметра
, и ограничиться оптимизацией всего одного глобального параметра  минимизирующего
ошибку:
минимизирующего
ошибку:
![E=-\langle\ln[1+\delta x_t y_t]\rangle](/sites/default/files/tex_cache/410d976a4bbf1eacd5d4eff7ed6adc50.png)
Тем самым, появляется возможность регулировать ставку в соответствии с уровнем риска, предсказываемым сетью. Игра с переменными
ставками приносит большую прибыль, чем игра с фиксированными ставками. Действительно, если зафиксировать ставку, определив ее по
средней предсказуемости, то скорость роста капитала будет пропорциональна  , тогда как если определять оптимальную ставку на каждом
шаге, то - пропорциональна
, тогда как если определять оптимальную ставку на каждом
шаге, то - пропорциональна  .
.


