Предсказание финансовых временных рядов
Формирование пространства признаков
Ключевым для повышения качества предсказаний является эффективное кодирование входной информации. Это особенно важно для труднопредсказуемых финансовых временных рядов. Все рекомендации, описанные в лекции о предобработке данных, применимы и здесь. Имеются, однако, и специфичные именно для финансовых временных рядов способы предобработки данных, на которых мы подробно остановимся в данном разделе.
Способы погружения временного ряда
Начнем с того, что в качестве входов и выходов нейросети не следует выбирать сами значения котировок, которые мы обозначим 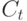 .
Действительно значимыми для предсказаний являются изменения котировок. Поскольку эти изменения, как правило, гораздо меньше по
амплитуде, чем сами котировки, между последовательными значениями курсов имеется большая корреляция - наиболее вероятное значение
курса в следующий момент равно его предыдущему значению:
.
Действительно значимыми для предсказаний являются изменения котировок. Поскольку эти изменения, как правило, гораздо меньше по
амплитуде, чем сами котировки, между последовательными значениями курсов имеется большая корреляция - наиболее вероятное значение
курса в следующий момент равно его предыдущему значению:  . Между тем, как это уже неоднократно подчеркивалось, для повышения качества
обучения следует стремиться к статистической независимости входов, то есть к отсутствию подобных корреляций.
. Между тем, как это уже неоднократно подчеркивалось, для повышения качества
обучения следует стремиться к статистической независимости входов, то есть к отсутствию подобных корреляций.
Поэтому в качестве входных переменных логично выбирать наиболее статистически независимые величины, например, изменения
котировок  или логарифм относительного приращения
или логарифм относительного приращения  . Последний выбор хорош для длительных временных рядов, когда уже заметно влияние
инфляции. В этом случае простые разности в разных частях ряда будут иметь различную амплитуду, т.к. фактически измеряются в различных
единицах. Напротив, отношения последовательных котировок не зависят от единиц измерения, и будут одного масштаба несмотря на
инфляционное изменение единиц измерения. В итоге, большая стационарность ряда позволит использовать для обучения большую историю и
обеспечит лучшее обучение.
. Последний выбор хорош для длительных временных рядов, когда уже заметно влияние
инфляции. В этом случае простые разности в разных частях ряда будут иметь различную амплитуду, т.к. фактически измеряются в различных
единицах. Напротив, отношения последовательных котировок не зависят от единиц измерения, и будут одного масштаба несмотря на
инфляционное изменение единиц измерения. В итоге, большая стационарность ряда позволит использовать для обучения большую историю и
обеспечит лучшее обучение.
Отрицательной чертой погружения в лаговое пространство является ограниченный "кругозор" сети. Технический анализ же, напротив, не фиксирует окно в прошлом, и пользуется подчас весьма далекими значениями ряда. Например, утверждается, что максимальные и минимальные значения ряда даже в относительно далеком прошлом оказывают достаточно сильное воздействие на психологию игроков, и, следовательно, должны быть значимы для предсказания. Недостаточно широкое окно погружения в лаговое пространство не способно предоставить такую информацию, что, естественно, снижает эффективность предсказания. С другой стороны, расширение окна до таких значений, когда захватываются далекие экстремальные значения ряда, повышает размерность сети, что в свою очередь приводит к понижению точности нейросетевого предсказания - уже из-за разрастания размера сети5Напомним, что согласно нашим прошлым оценкам минимальная ошибка нейропредсказаний возрастает с ростом числа входов: , где - число примеров.
Выходом из этой, казалось бы, тупиковой ситуации являются альтернативные способы кодирования прошлого поведения ряда. Интуитивно понятно, что чем дальше в прошлое уходит история ряда, тем меньше деталей его поведения влияет на результат предсказаний. Это обосновано психологией субъективного восприятия прошлого участниками торгов, которые, собственно, и формируют будущее. Следовательно, надо найти такое представление динамики ряда, которое имело бы избирательную точность: чем дальше в прошлое - тем меньше деталей, при сохранении общего вида кривой. Весьма перспективным инструментом здесь может оказаться т.н. вейвлетное разложение (wavelet decomposition). Оно эквивалентно по информативности лаговому погружению, но легче допускает такое сжатие информации, которое описывает прошлое с избирательной точностью.
Понижение размерности входов: признаки
Подобного рода сжатие информации является примером извлечения из непомерно большого числа входных переменных наиболее значимых для предсказания признаков. Способы систематического извлечения признаков уже были описаны в прошлых лекциях. Их можно (и нужно) с успехом применять и к предсказанию временных рядов.
Важно только, чтобы способ представления входной информации по возможности облегчал процесс извлечения признаков. Вейвлетное представление являет собой пример удачного, с точки зрения извлечения признаков, кодирования (Kaiser, 1995). Например, на следующем рисунке ( рисунок 8.6) изображен отрезок из 50 значений ряда вместе с его реконструкцией по 10 специальным образом отобранным вейвлет-коэффициентов. Обратите внимание, что несмотря на то, что для этого потребовалось в пять раз меньше данных, непосредственное прошлое ряда восстановлено точно, а более далекое - лишь в общих чертах, хотя максимумы и минимумы отражены верно. Следовательно, можно с приемлемой точностью описывать 50-мерное окно всего лишь 10-мерным входным вектором.
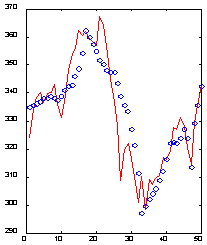
Рис. 8.6. Пример 50-мерного окна (сплошная линия) и его реконструкции по 10 вейвлет-коэффициентам (о)
Еще один возможный подход - использование в качестве возможных кандидатов в пространство признаков различного рода индикаторов технического анализа, которые автоматически подсчитываются в соответствующих программных пакетах (таких как MetaStock или Windows On Wall Street). Многочисленность этих эмпирических признаков (Colby, 1988) затрудняет пользование ими, тогда как каждый из них может оказаться полезным в применении к данному ряду. Описанные ранее методы позволят отобрать наиболее значимую комбинацию технических индикаторов, которую и следует затем использовать в качестве входов нейросети.
