Обучение без учителя: Сжатие информации
Оценка вычислительной сложности обучения
В этой лекции мы рассмотрели два разных типа обучения, основанные на разных принципах кодирования информации выходным слоем нейронов. Логично теперь сравнить их по степени вычислительной сложности и выяснить когда выгоднее применять понижение размерности, а когда - квантование входной информации.
Как мы видели, алгоритм обучения сетей, понижающих размерность, сводится к обычному обучению с учителем, сложность которого была
оценена ранее. Такое обучение требует  операций, где
операций, где  - число синаптических весов сети, а
- число синаптических весов сети, а  - число обучающих примеров. Для однослойной
сети с
- число обучающих примеров. Для однослойной
сети с  входами и
входами и  выходными нейронами число весов равно
выходными нейронами число весов равно 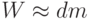 и сложность обучения
и сложность обучения  можно оценить как
можно оценить как 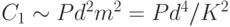 , где
, где 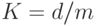 - коэффициент сжатия
информации.
- коэффициент сжатия
информации.
Кластеризация или квантование требуют настройки гораздо большего количества весов - из-за неэффективного способа кодирования.
Зато такое избыточное кодирование упрощает алгоритм обучения. Действительно, квадратичная функция ошибки в этом случае диагональна,
и в принципе достижение минимума возможно за  шагов (например в пакетном режиме), что в данном случае потребует
шагов (например в пакетном режиме), что в данном случае потребует 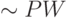 операций. Число
весов, как и прежде, равно
операций. Число
весов, как и прежде, равно 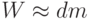 , но степень сжатия информации в данном случае определяется по-другому:
, но степень сжатия информации в данном случае определяется по-другому: 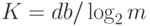 . Сложность обучения как функция
степени сжатия запишется в виде:
. Сложность обучения как функция
степени сжатия запишется в виде: 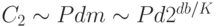 .
.
При одинаковой степени сжатия, отношение сложности квантования к сложности данных снижения размерности запишется в виде:
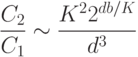
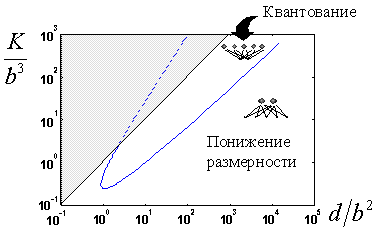
Наибольшее сжатие возможно методом квантования, но из-за экспоненциального роста числа кластеров, при большой размерности данных
выгоднее использовать понижение размерности. Максимальное сжатие при понижении размерности равно 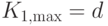 , тогда как квантованием можно достичь
сжатия
, тогда как квантованием можно достичь
сжатия 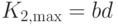 (при двух нейронах-прототипах). Область недостижимых сжатий
(при двух нейронах-прототипах). Область недостижимых сжатий 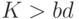 показана на рисунке серым.
показана на рисунке серым.
В качестве примера рассмотрим типичные параметры сжатия изображений в формате JPEG. При этом способе сжатия изображение
разбивается на квадраты со стороной  пикселей, которые и являются входными векторами, подлежащими сжатию. Следовательно, в данном
случае
пикселей, которые и являются входными векторами, подлежащими сжатию. Следовательно, в данном
случае 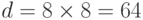 . Предположим, что картинка содержит
. Предположим, что картинка содержит  градаций серого цвета, т. е. точность представления данных
градаций серого цвета, т. е. точность представления данных 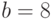 . Тогда координата абсциссы на
приведенном выше графике будет
. Тогда координата абсциссы на
приведенном выше графике будет  . Как следует из графика при любых допустимых степенях сжатия в данном случае оптимальным с точки
зрения вычислительных затрат является снижение размерности3Действительно, JPEG при ближайшем рассмотрении имеет много общего с методом главных компонент.
. Как следует из графика при любых допустимых степенях сжатия в данном случае оптимальным с точки
зрения вычислительных затрат является снижение размерности3Действительно, JPEG при ближайшем рассмотрении имеет много общего с методом главных компонент.
Однако, при увеличении размеров элементарного блока, появляется область высоких степеней сжатия, достижимых лишь с
использованием квантования. Скажем, при 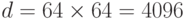 , когда
, когда 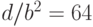 , в соответствии с графиком
(см. рисунок 4.11), квантование следует применять для сжатия более
, в соответствии с графиком
(см. рисунок 4.11), квантование следует применять для сжатия более 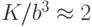 , т. е.
, т. е. 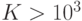 .
.
Победитель забирает не все
Один из вариантов модификации базового правила обучения соревновательного слоя состоит в том, чтобы обучать не только нейрон-победитель, но и его "соседей", хотя и с меньшей скоростью. Такой подход - "подтягивание" ближайших к победителю нейронов - применяется в топографических картах Кохонена. В силу большой практической значимости этой нейросетевой архитектуры, остановимся на ней более подробно.