Обучение без учителя: Сжатие информации
Нелинейный анализ главных компонент
Целевая функция
Наглядной демонстрацией полезности нелинейного анализа главных компонент является следующий простой пример (см. рисунок 4.7).
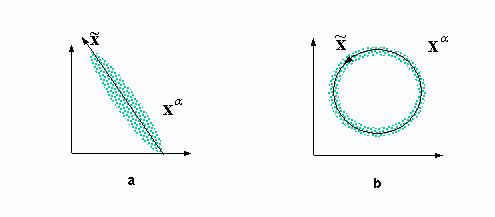
Рис. 4.7. Анализ главных компонент дает линейное подпространство, минимизирующее отклонение данных (a). Он не способен, однако, выявить одномерный характер распределения данных в случае (b). Для их одномерной параметризации нужны нелинейные координаты
Он показывает, что в общем случае нас интересует нелинейное преобразование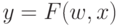 
, 
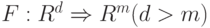, сохраняющее максимальное количество
информации о распределении данных в обучающей выборке 
и являющееся наиболее сжатым представлением этих данных. Такое представление
данных, не поддающееся дальнейшему сжатию, обладает максимальной энтропией, т.е. их статистическое распределение не отличимо от
случайного шума. Таким образом, в общем случае целевой функцией при сжатии данных является максимизация энтропии: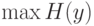 
. Естественно, при
этом предполагается ограниченность диапазона изменения выходов, например: ![y\in [0,1]^m](/sites/default/files/tex_cache/11f2fd135c8f1ef8dfd556663543f4af.png)
во избежании неограниченного роста энтропии2Энтропия случайной величины по порядку равна логарифму характерного разброса ее значений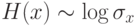 
Автоассоциативные сети
Весьма общим подходом к понижению размерности является использование нелинейных автоассоциативных сетей. В общем случае они должны содержать как минимум три скрытых слоя нейронов. Средний слой - узкое горло, будет в результате обучения выдавать сжатое представление данных . Первый скрытый слой нужен для осуществления произвольного нелинейного кодирования, а последний - для нахождения соответствующего декодера (рисунок 4.8).
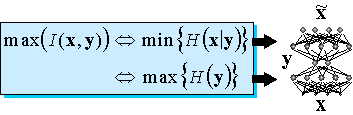
Рис. 4.8. Понижение размерности с помощью автоассоциативных сетей. Минимизация ошибки воспроизведения сетью своих входов эквивалентна оптимальному кодированию в узком горле сети
Задачей автоассоциативных сетей, как уже говорилось, является воспроизведение на выходе сети значений своих входов. Вторая
половина сети - декодер - при этом опирается лишь на кодированную информацию в узком горле сети. Качество воспроизведения данных по
их кодированному представлению измеряется условной энтропией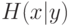 
. Чем она меньше, тем меньше неопределенность, т. е. лучше воспроизведение.
Нетрудно показать, что минимизация неопределенности эквивалентна максимизации энтропии кодирования:
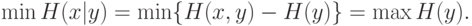
Действительно, механическая процедура кодирования не вносит дополнительной неопределенности, так что совместная энтропия входов
и их кодового представления равна энтропии самих входов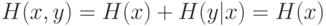 
и, следовательно, не зависит от параметров сети.
Привлекательной чертой такого подхода к сжатию информации является его общность. Однако многочисленные локальные минимумы и трудоемкость обучения существенно снижают его практическую ценность.
Более компактные схемы сжатия обеспечивает метод предикторов.
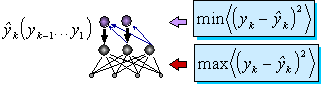
Предикторы
Условие максимизации совместной энтропии выходов можно переписать в виде:
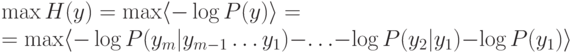
Обозначим 
. выход сети-предиктора, предсказывающей значение переменной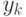 
.. Целевой функцией
такой сети будет минимизация ошибки предсказания:
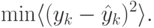
, основная сеть будет, напротив, максимизировать отклонение от предсказаний, ставя себе целью: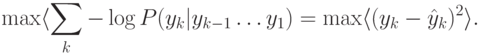
Таким образом, во взаимном соревновании основная и дополнительные сети обеспечивают постепенное выявление статистически независимых признаков, осуществляющих оптимальное кодирование.
Размер сетей-предикторов определяется количеством выходов сети m, так что их суммарный объем, как правило, много меньше, чем размер декодера в автоассоциативной сети, определяемый числом входов d. В этом и состоит основное преимущество данного подхода.
Латеральные связи
Предикторы вводят связи между признаками, обеспечивающие их статистическую независимость. В частном случае линейных предикторов дополнительные сети вырождаются в латеральные связи между нейронами последнего слоя. Эти связи обучаются таким образом, чтобы выходы нейронов этого слоя были некоррелированы.
Между тем, можно предложить и такую схему латеральных связей, которая, наоборот, обеспечивает максимальную коррелированность выходов. Допустим, например, что выход каждого нейрона подается на его вход с положительным весом, а на вход остальных нейронов слоя - с отрицательным. Тем самым, каждый нейрон будет усиливать свой выход и подавлять активность остальных. При логистической функции активации, препятствующей бесконечному росту, победителем в этой борьбе выйдет нейрон с максимальным первоначальным значением выхода. Его значение возрастет до единицы, а активность остальных нейронов затухнет до нуля.
Такие соревновательные слои нейронов также можно использовать для сжатия информации, но это сжатие будет основано на совершенно других принципах.