Обучение без учителя: Сжатие информации

Взаимодействие нейронов: анализ главных компонент

Единственный нейрон осуществляет предельное сжатие многомерной информации, выделяя лишь одну скалярную характеристику многомерных данных. Каким бы оптимальным ни было сжатие информации, редко когда удается полностью охарактеризовать многомерные данные всего одним признаком. Однако, наращиванием числа нейронов можно увеличить выходную информацию. В этом разделе мы обобщим найденное ранее правило обучения на случай нескольких нейронов в самообучающемся слое, опираясь на отмеченную выше аналогию с автоассоциативными сетями.

Постановка задачи

Итак, пусть теперь на том же наборе d-мерных данных обучается m линейных нейронов:

Мы хотим, чтобы амплитуды выходных нейронов были набором независимых индикаторов, максимально полно отражающих информацию о многомерном входе сети.

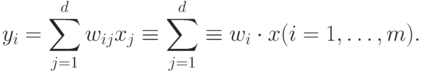
Необходимость взаимодействия нейронов

Если мы просто поместим несколько нейронов в выходной слой и будем обучать каждый из них независимо от других, мы добьемся лишь многократного дублирования одного и того же выхода. Очевидно, что для получения нескольких содержательных признаков на выходе исходное правило обучения должно быть каким-то образом модифицировано - за счет включения взаимодействия между нейронами.

Самообучающийся слой

В нашей трактовке правила обучения отдельного нейрона, последний пытается воспроизвести значения своих входов по амплитуде своего выхода. Обобщая это наблюдение, логично было бы предложить правило, по которому значения входов восстанавливаются по всей выходной информации. Следуя этой линии рассуждений получаем правило Ойа для однослойной сети:

или в векторном виде:

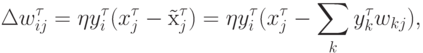
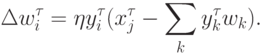
Такое обучение эквивалентно сети с узким горлом из скрытых линейных нейронов, обученной воспроизводить на выходе значения своих входов.

Скрытый слой такой сети, так же как и слой Ойа, осуществляет оптимальное кодирование входных данных, и содержит максимально возможное при данных ограничениях количество информации.

Сравнение с традиционным статистическим анализом

Вывод о способности нейронных сетей самостоятельно выделять наиболее значимые признаки в потоках информации, обучаясь по очень простым локальным правилам, важен с общенаучной точки зрения. Изучение этих механизмов помогает глубже понять как функционирует мозг. Однако есть ли в описанных выше нейроалгоритмах какой-нибудь практический смысл?

Действительно, для этих целей существуют хорошо известные алгоритмы стандартного статистического анализа. В частности, анализ главных компонент также выделяет основные признаки, осуществляя оптимальное линейное сжатие информации. Более того, можно показать, что сжатие информации слоем Ойа эквивалентно анализу главных компонент . Это и не удивительно, поскольку оба метода оптимальны при одних и тех же ограничениях.

Однако стандартный анализ главных компонент дает решение в явном виде, через последовательность матричных операций, а не итерационно, как в случае нейросетевых алгоритмов. Так что при отсутствии высокопараллельных нейроускорителей на практике удобнее пользоваться матричными методами, а не обучать нейросети. Есть ли тогда практический смысл в изложенных выше итеративных нейросетевых алгоритмах?

Конечно же есть, по крайней мере по двум причинам:

• Во-первых, иногда обучение необходимо проводить в режиме on-line, т. е. на ходу адаптироваться к меняющемуся потоку данных. Примером может служить борьба с нестационарными помехами в каналах связи. Итерационные методы идеально подходят в этой ситуации, когда нет возможности собрать воедино весь набор примеров и произвести необходимые матричные операции над ним.
• Во-вторых, и это, видимо, главное, нейроалгоритмы легко обобщаются на случай нелинейного сжатия информации, когда никаких явных решений уже не существует. Никто не мешает нам заменить линейные нейроны в описанных выше сетях - нелинейными. С минимальными видоизменениями нейроалгоритмы будут работать и в этом случае, всегда находя оптимальное сжатие при наложенных нами ограничениях. Таким образом, нейроалгоритмы представляют собой удобный инструмент нелинейного анализа, позволяющий относительно легко находить способы глубокого сжатия информации и выделения нетривиальных признаков.

Иногда,даже простая замена линейной функции активации нейронов на сигмоидную в найденном выше правиле обучения:

приводит к новому качеству (Oja, et al, 1991). Такой алгоритм, в частности, с успехом применялся для разделения смешанных неизвестным образом сигналов (т. н. blind signal separation). Эту задачу каждый из нас вынужден решать, когда хочет выделить речь одного человека в шуме общего разговора.

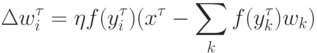
Однако нас здесь интересуют не конкретные алгоритмы, а, скорее, общие принципы выделения значимых признаков, на которых имеет смысл остановиться несколько более подробно.