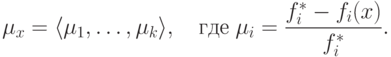|
Зачем необходимы треугольные нормы и конормы? Как их использовать? Имеется ввиду, на практике. |
Методы построения функции принадлежности. Обзор основных методов
Прямые методы для одного эксперта
Прямые методы для одного эксперта состоят в непосредственном задании
функции,
позволяющей вычислять значения. Например, пусть переменная
"ВОЗРАСТ"
принимает значения из интервала ![U = [0,100]](/sites/default/files/tex_cache/a308586c52ce786f8cc1acca1fc58c74.png) . Слово
"МОЛОДОЙ" можно
интерпретировать как имя нечеткого подмножества
. Слово
"МОЛОДОЙ" можно
интерпретировать как имя нечеткого подмножества  , которое
характеризуется
функцией совместимости. Таким образом, степень, с которой численное значение
возраста,
скажем
, которое
характеризуется
функцией совместимости. Таким образом, степень, с которой численное значение
возраста,
скажем 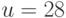 , совместимо с понятием "МОЛОДОЙ", есть
, совместимо с понятием "МОЛОДОЙ", есть 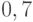 , в то время
как совместимость
, в то время
как совместимость 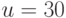 и
и 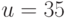 с тем же понятием
есть
с тем же понятием
есть  и
и 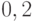 соответственно.
соответственно.
Рассмотрим предложенный Осгудом метод семантических дифференциалов. Практически в любой области можно получить множество шкал оценок, используя следующую процедуру:
- определить список свойств, по которым оценивается понятие (объект);
- найти в этом списке полярные свойства и сформировать полярную шкалу;
- для каждой пары полюсов оценить, в какой степени введенное понятие обладает положительным свойством.
Совокупность оценок по шкалам была названа профилем понятия.
Следовательно, вектор с координатами, изменяющимися от  до
до  , также называется
профилем. Профиль есть нечеткое подмножество положительного
списка свойств или шкал.
, также называется
профилем. Профиль есть нечеткое подмножество положительного
списка свойств или шкал.
Пример. В задаче распознавания лиц можно выделить следующие шкалы:
 |
Высота лба | Низкий-широкий |
 |
Профиль носа | Горбатый-курносый |
 |
Длина носа | Короткий-длинный |
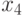 |
Разрез глаз | Узкие-широкие |
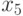 |
Цвет глаз | Темные-светлые |
 |
Форма подбородка | Остроконечный-квадратный |
 |
Толщина губ | Тонкие-толстые |
 |
Цвет лица | Смуглое-светлое |
 |
Очертание лица | Овальное-квадратное |
Светлое квадратное лицо, у которого чрезвычайно широкий лоб, курносый
длинный нос, широкие светлые глаза, остроконечный подбородок, может
быть определено как нечеткое множество 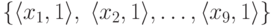 .
.
Способ вычисления частичной принадлежности друг другу строгих
множеств.
Пусть покрытием  обычного множества
обычного множества  является
любая совокупность
обычных подмножеств
является
любая совокупность
обычных подмножеств 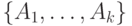 множества
множества  таких,
что
таких,
что  . В крайнем
случае, когда для любых
. В крайнем
случае, когда для любых 
 ,
,  ,
имеет место разбиение
,
имеет место разбиение  . Предположим, что имеется
. Предположим, что имеется 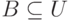 , тогда
, тогда  может рассматриваться как нечеткое подмножество
может рассматриваться как нечеткое подмножество  с функцией
принадлежности
с функцией
принадлежности
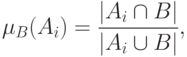
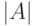 — мощность множества
— мощность множества  .
.Пример.
Пусть 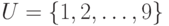 ,
, 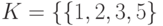 ,
, 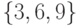 ,
, 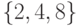 ,
,  ,
, 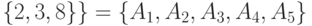 ,
, 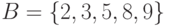 . Тогда,
рассматривая
. Тогда,
рассматривая  как нечеткое подмножество
как нечеткое подмножество  ,
можно написать
,
можно написать

Любое решение задачи многоцелевой оптимизации можно рассматривать как
нечеткое
подмножество значений целевой функции следующим образом. Пусть 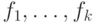 —
целевые функции, где
—
целевые функции, где 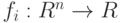 , и пусть требуется решить
задачу
, и пусть требуется решить
задачу 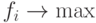 для всех
для всех  . Пусть
. Пусть 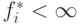 —
максимальное значение функции
—
максимальное значение функции 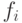 и
и 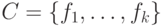 —
множество целевых функций, тогда любое значение
—
множество целевых функций, тогда любое значение  в области
определения
в области
определения 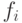 можно рассматривать как нечеткое множество на
можно рассматривать как нечеткое множество на  с вектором
значений принадлежности
с вектором
значений принадлежности