|
Постройте таблицу значений функции |
Работа с файловыми потоками. Пользовательские функции
Занятие 2. Пользовательские функции
Ранее в программах мы использовали функции из разных библиотек, например, 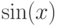 из библиотеки <math.h> или setw(10) из библиотеки <iomanip>. Что общего во всех функциях? Все функции представляют собой некий шаблон, по которому вычисляется значение какой-то функции или выполняется набор каких-то действий. В языке С++ есть возможность создавать свои функции, не относящиеся к библиотекам. Такие функции называются пользовательскими функциями.
из библиотеки <math.h> или setw(10) из библиотеки <iomanip>. Что общего во всех функциях? Все функции представляют собой некий шаблон, по которому вычисляется значение какой-то функции или выполняется набор каких-то действий. В языке С++ есть возможность создавать свои функции, не относящиеся к библиотекам. Такие функции называются пользовательскими функциями.
Для того, чтобы создать и использовать свою пользовательскую функцию в программе, необходимо:
- объявить пользовательскую функцию:
здесь тип_данных – это возвращаемый тип данных функции, который определяется ответом функции (выходные данные), имя функции – любое имя (по аналогии с именем переменной), список параметров – это то, с чем наша функция будет работать (входные данные);
тип_данных имя_функции (список параметров);
- описать пользовательскую функцию;
- вызвать пользовательскую функцию.
Объявление пользовательской фукнции должно быть обязательно до функции main(), описание может быть вместе с объявлением, а может быть после функции main(). Вызов пользовательской функции может быть внутри функции main() или внутри другой пользовательской функции.
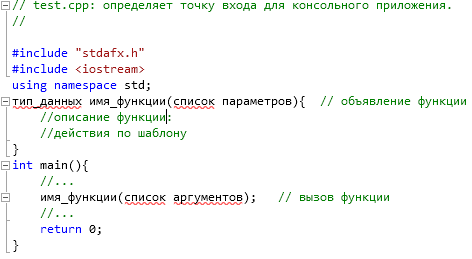
Первый вариант описания пользовательской функции – до функции main() представлен на рис. 7.4.
Второй вариант описания пользовательской функции – после функции main() представлен на рис. 7.5.
Конечно, приведенные выше варианты не заработают, т.к. они показывают общую структуру записи программ. В наших примерах всегда будем использовать первый вариант.
Вообще говоря, любую функцию следует воспринимать как некий воображаемый аппарат для выполнения какой-либо работы. При этом аппарату нужно работать над каким-то материалом, т.е. входными данными, известными заранее. Этими данными являются параметры функции. Когда аппарат получил материал, то начинает свою работу. Какую именно работу он будет выполнять с входным материалом, зависит от шаблона, т.е. от описания функции. После того, как вся работа будет выполнена, аппарат выдаст нам результат своей работы, некий ответ. Это то, ради чего мы и создавали этот аппарат. Схемотично данный процесс представлен на рис. 7.6.
Например, для известной нам функции 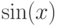 из библиотеки <math.h>, входными данными является один параметр – вещественное число
из библиотеки <math.h>, входными данными является один параметр – вещественное число  , сам аппарат представляет собой процесс вычисления синуса от
, сам аппарат представляет собой процесс вычисления синуса от  , результатом является полученное значение синуса. Результат является вещественным числом, которое задается ключевым словом double. Поэтому можно было бы представить объявление и описание функции
, результатом является полученное значение синуса. Результат является вещественным числом, которое задается ключевым словом double. Поэтому можно было бы представить объявление и описание функции 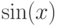 следующим образом:
следующим образом:
double sin(double x){
double res;
res=...; // вычисление синуса по сложной математической формуле
return res; // ответ, результат
}Здесь внутри функции объявлена локальная переменная double res, в которую будет насчитываться ответ (res – result – результат). Данная переменная будет видна только внутри пользовательской функции. Переменная res – это, своего рода, временная переменная для расчета синуса. Строка return res; выдает в ответ вычисленное значение синуса.
Вызов функции 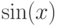 внутри функции main() выглядит следующим образом:
внутри функции main() выглядит следующим образом:
z=sin(1.5);
Примечание. Хотелось бы обратить внимание на разницу между списком параметров при объявлении функции и список аргументов при вызове функции. Объявление, описание и список формальных параметров составляют весь шаблон. Здесь параметры представляют собой некие абстрактные параметры, которые пока нельзя "пощупать". А вот когда идет вызов функции, абстрактные параметры приобретают вполне реальные формы и становятся аргументами функции, конкретными числами. В программе это отражается следущим образом. Объявление и описание функции делается один раз:
double function(double a, double b){...}Вызовов функции может быть сколько угодно:
int main(){
double x, y, z1, z2, z3;
x=10;
y=-0.3;
z1=function(x,y); // первый вариант вызова
z2=function(1.8, y); // второй вариант вызова
z3=function(1.8, 0); // третий вариант вызова
return 0;
}Рассмотрим несколько примеров по созданию пользовательских функций.
Пример 1. Требуется создать пользовательскую функцию для вычисления квадрата вещественного числа.
Решение. Составим схему работы нашей пользовательской функции в общем виде на рис. 7.7.
Т.к. параметр х должен быть вещественным, то ему соответствует тип double. Пользовательская функция должна считать квадрат числа, поэтому назовем ее kv. В ответ будет выдаваться вещественное число, поэтому возвращаемый тип у функции будет double.
Объявление и описание функции kv:
double kv(double x){
double res;
res=x*x;
return res;
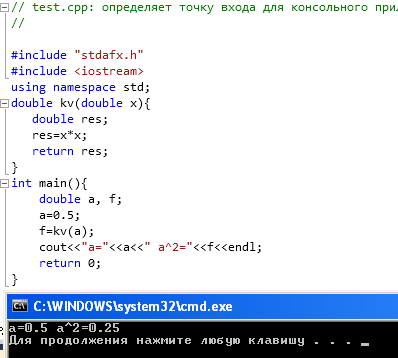
}Код программы и результат выполнения программы:
Пример 2. Вычислить таблицу " " значений функции
" значений функции 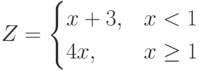 при
при 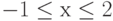 с шагом 1.
с шагом 1.
Решение. Сделаем пользовательскую функцию для вычисления значения функции  . Возвращаемый тип – double, т.к. ответом является вещественное число. Параметр один, double x. В описании пользовательской функции будет вычисление функции по разветвляющемуся алгоритму. В функции main() реализуем циклический алгоритм для вывода таблицы значений функции.
. Возвращаемый тип – double, т.к. ответом является вещественное число. Параметр один, double x. В описании пользовательской функции будет вычисление функции по разветвляющемуся алгоритму. В функции main() реализуем циклический алгоритм для вывода таблицы значений функции.
// test.cpp: определяет точку входа для консольного приложения.
//
#include "stdafx.h"
#include <iostream>
#include <iomanip>
using namespace std;
double fz(double x){
double res;
if(x<1){
res=x+3.0;
}
else {
res=4.0*x;
}
return res;
}
int main(){
double x, z;
cout<<setw(10)<<"x"<<setw(10)<<"z"<<endl;
for(x=-1; x<=2; x=x+1){
z=fz(x);
cout<<setw(10)<<x<<setw(10)<<z<<endl;
}
return 0;
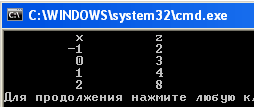
}Результат выполнения программы:
Пример 3. Вычислить таблицу " " значений функции
" значений функции 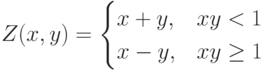 при
при  с шагом 1,
с шагом 1,  с шагом 5 .
с шагом 5 .
Решение. Сделаем пользовательскую функцию для вычисления значения функции  . Возвращаемый тип – double, т.к. ответом является вещественное число. Параметров два, double x, double y. В описании пользовательской функции будет вычисление функции по разветвляющемуся алгоритму. В функции main() реализуем вложенные циклы для вывода таблицы значений функции.
. Возвращаемый тип – double, т.к. ответом является вещественное число. Параметров два, double x, double y. В описании пользовательской функции будет вычисление функции по разветвляющемуся алгоритму. В функции main() реализуем вложенные циклы для вывода таблицы значений функции.
// test.cpp: определяет точку входа для консольного приложения.
//
#include "stdafx.h"
#include <iostream>
#include <iomanip>
using namespace std;
double fz(double x, double y){
double res;
if(x*y<1){
res=x+y;
}
else {
res=x-y;
}
return res;
}
int main(){
double x, y, z;
cout<<setw(10)<<"x"<<setw(10)<<"y"<<setw(10)<<"z"<<endl;
for(x=-1; x<=0.5; x=x+1){
for(y=5; y<=15; y=y+5){
z=fz(x, y);
cout<<setw(10)<<x<<setw(10)<<y<<setw(10)<<z<<endl;
}
}
return 0;
}Результат выполнения программы:
Пример 4. Вычислить таблицу значений функции 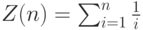 при
при 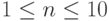 с шагом 1.
с шагом 1.
Решение. Сделаем пользовательскую функцию для вычисления значения функции  . Возвращаемый тип – double, т.к. ответом является вещественное число. Параметр один, int n. В описании пользовательской функции будет вычисление функции по циклическому алгоритму. В функции main() реализуем цикл по
. Возвращаемый тип – double, т.к. ответом является вещественное число. Параметр один, int n. В описании пользовательской функции будет вычисление функции по циклическому алгоритму. В функции main() реализуем цикл по  для вывода таблицы значений функции.
для вывода таблицы значений функции.
// test.cpp: определяет точку входа для консольного приложения.
//
#include "stdafx.h"
#include <iostream>
#include <iomanip>
using namespace std;
double fz(int n){
double res;
int i;
res=0;
for(i=1; i<=n; i=i+1){
res=res+1.0/i;
}
return res;
}
int main(){
int n;
double z;
cout<<setw(10)<<"n"<<setw(10)<<"z"<<endl;
for(n=1; n<=10; n=n+1){
z=fz(n);
cout<<setw(10)<<n<<setw(10)<<z<<endl;
}
return 0;
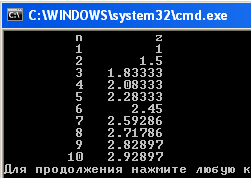
}Результат выполнения программы:
Пример 5. Создать пользовательскую функцию для вывода массива из 5 строк и 5 столбцов на экран.
Решение. Пользовательскую функцию назовем print_mass. В качестве параметра будет сам массив, например, double х[5][5]. Результатом пользовательской функции является вывод массива на экран, поэтому никакого числа в ответе не будет. Следовательно, возвращаемый тип на этот раз будет void, что означает "пустой". В описании пользовательской функции организуем вывод двумерного массива во вложенном цикле. В функции main() инициализируем два массива ![A[5][5], B[5][5]](/sites/default/files/tex_cache/9f96b7779620ee3b80025cacc7329b11.png) и вызовем функцию print_mass два раза.
и вызовем функцию print_mass два раза.
// test.cpp: определяет точку входа для консольного приложения.
//
#include "stdafx.h"
#include <iostream>
#include <iomanip>
using namespace std;
void print_mass(double x[5][5]){
int i, j;
for(i=0; i<5; i=i+1){
for(j=0; j<5; j=j+1){
cout<<setw(10)<<x[i][j];
}
cout<<endl;
}
}
int main(){
double A[5][5], B[5][5];
int i,j;
for(i=0; i<5; i=i+1){
for(j=0; j<5; j=j+1){
A[i][j]=2.3*i+j;
B[i][j]=i-1.5*j;
}
}
cout<<"massiv A:"<<endl;
print_mass(A);
cout<<"massiv B:"<<endl;
print_mass(B);
return 0;
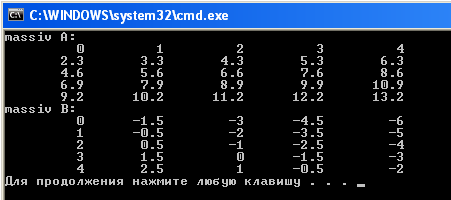
}Результат выполнения программы:
Пример 6. Массив ![А[5][5]](/sites/default/files/tex_cache/7748d44414eb52cfd8ab1c70b469ef8c.png) задан по формуле
задан по формуле ![А[i][j]=0,3i-j](/sites/default/files/tex_cache/aab494af4b31ddf35210c3f5f1766852.png) , массив
, массив ![B[5][5]](/sites/default/files/tex_cache/0dfb33e23efe6d24c20e2872ceaba737.png) по формуле
по формуле ![B[i][j]=i-1.5j](/sites/default/files/tex_cache/4710dd38f33d2160996923aa4f907e90.png) . Вычислить сумму положительных элементов массивов.
. Вычислить сумму положительных элементов массивов.
Решение. Создадим пользовательскую функцию для вычисления суммы положительных элементов массива, назовем ее sum_pol. В качестве параметра будет формальный массив ![x[5][5]](/sites/default/files/tex_cache/70649b64d25a7f9b007bbe4168a786b1.png) . В функции main() проинициализируем массивы
. В функции main() проинициализируем массивы  и
и  , затем два раза вызовем функцию sum_pol.
, затем два раза вызовем функцию sum_pol.
// test.cpp: определяет точку входа для консольного приложения.
//
#include "stdafx.h"
#include <iostream>
#include <iomanip>
using namespace std;
double sum_pol(double x[5][5]){
int i, j;
double s;
s=0;
for(i=0; i<5; i=i+1){
for(j=0; j<5; j=j+1){
if(x[i][j]>0){ s=s+x[i][j];}
}
}
return s;
}
int main(){
double A[5][5], B[5][5], sa, sb;
int i,j;
for(i=0; i<5; i=i+1){
for(j=0; j<5; j=j+1){
A[i][j]=0.3*i+j;
B[i][j]=i-1.5*j;
}
}
sa=sum_pol(A);
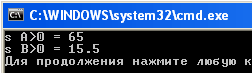
cout<<"s A>0 = "<<sa<<endl;
sb=sum_pol(B);
cout<<"s B>0 = "<<sb<<endl;
return 0;
}Результат выполнения программы:
Краткие итоги
Чтобы работать с файлами, необходимо использовать переменную типа fstream. Рассмотрены случаи вывода в файл и чтения из файла.
Вопросы
- Что такое файловый поток?
- Что необходимо сделать, чтобы использовать в программе файловый поток?
- Как сделать разделение по ячейкам при записи в файл *.xls?
- Что такое пользовательская функция?
- Что такое объявление, описание, вызов пользовательской функции?
Упражнения
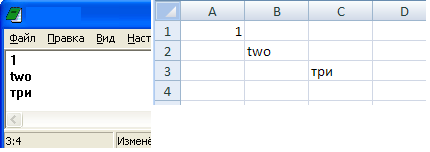
- Составьте программу, которая создаст следующие файлы:
- Составьте блок-схему и программу для построения таблицы значений функции
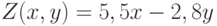 при
при 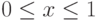 с шагом
с шагом 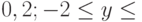 0 с шагом 0,8. Таблицы вывести на экран, в файлы *.txt, *.xls.
0 с шагом 0,8. Таблицы вывести на экран, в файлы *.txt, *.xls. - Для массива
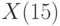 найти минимальный элемент, максимальный элемент; найденные минимальный и максимальный элементы поменять местами. Исходный массив
найти минимальный элемент, максимальный элемент; найденные минимальный и максимальный элементы поменять местами. Исходный массив 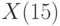 считать из файла. Исходный массив, результаты вычислений и измененный массив вывести на экран и в файл *.xls.
считать из файла. Исходный массив, результаты вычислений и измененный массив вывести на экран и в файл *.xls. - Составить блок-схему и программу для вычисления суммы 20 чисел из файла. Указание: использовать циклический алгоритм, не использовать массивы.
- В программе для задачи 3 создать пользовательские функции для вычисления минимального и максимального элементов.
- Массив
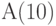 считать из файла. Вывести массив
считать из файла. Вывести массив  на экран. Поменять местами первый и последний элементы. Измененный массив вывести на экран. Указание: для вывода массива на экран создать пользовательскую функцию.
на экран. Поменять местами первый и последний элементы. Измененный массив вывести на экран. Указание: для вывода массива на экран создать пользовательскую функцию.





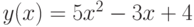 при
при 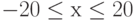 с шагом 0,5. Определите наименьшее значение функции и значение
с шагом 0,5. Определите наименьшее значение функции и значение  , при котором оно достигается.
, при котором оно достигается.