|
Постройте таблицу значений функции |
Понятие алгоритма. Виды алгоритмов
Существует несколько определений понятия алгоритма. Приведем два самых распространенных.
Алгоритм – последовательность чётко определенных действий, выполнение которых ведёт к решению задачи. Алгоритм, записанный на языке машины, есть программа решения задачи.
Алгоритм – это совокупность действий, приводящих к достижению результата за конечное число шагов.
Вообще говоря, первое определение не передает полноты смысла понятия алгоритм. Используемое слово "последовательность" сужает данное понятие, т.к. действия не обязательно должны следовать друг за другом – они могут повторяться или содержать условие.
Свойства алгоритмов:
- Дискретность (от лат. discretus — разделенный, прерывистый) – это разбиение алгоритма на ряд отдельных законченных действий (шагов).
- Детерминированность (от лат. determinate — определенность, точность) - любое действие алгоритма должно быть строго и недвусмысленно определено в каждом случае. Например, алгоритм проезда к другу, если к остановке подходят автобусы разных маршрутов, то в алгоритме должен быть указан конкретный номер маршрута 5. Кроме того, необходимо указать точное количество остановок, которое надо проехать, скажем, три.
- Конечность – каждое действие в отдельности и алгоритм в целом должны иметь возможность завершения.
- Массовость – один и тот же алгоритм можно использовать с разными исходными данными.
- Результативность – алгоритм должен приводить к достоверному решению.
Основная цель алгоритмизации – составление алгоритмов для ЭВМ с дальнейшим решением задачи на ЭВМ.
Примеры алгоритма:
- Любой прибор, купленный в магазине, снабжается инструкцией по его использованию. Данная инструкция и является алгоритмом для правильной эксплуатации прибора.
- Каждый шофер должен знать правила дорожного движения. Правила дорожного движения однозначно регламентируют поведение каждого участника движения. Зная эти правила, шофер должен действовать по определенному алгоритму.
- Массовый выпуск автомобилей стал возможен только тогда, когда был придуман порядок сборки машины на конвейере. Определенный порядок сборки автомобилей – это набор действий, в результате которых получается автомобиль.
Существует несколько способов записи алгоритмов. На практике наиболее распространены следующие формы представления алгоритмов:
- словесная (запись на естественном языке);
- псевдокоды (полуформализованные описания алгоритмов на условном алгоритмическом языке, включающие в себя как элементы языка программирования, так и фразы естественного языка, общепринятые математические обозначения и др.);
- графическая (изображения из графических символов – блок-схема);
- программная (тексты на языках программирования – код программы).
Рассмотрим подробно каждый вариант записи алгоритмов на примере следующей задачи. Требуется найти частное двух чисел.
Словесный способ записи алгоритмов представляет собой описание последовательных этапов обработки данных. Алгоритм задается в произвольном изложении на естественном языке. Ответ при этом получает человек, который выполняет команды согласно словесной записи.
Пример словесной записи:
- задать два числа, являющиеся делимым и делителем;
- проверить, равняется ли делитель нулю;
- если делитель не равен нулю, то найти частное, записать его в ответ;
- если делитель равен нулю, то в ответ записать "нет решения".
Словесный способ не имеет широкого распространения, так как такие описания: строго не формализуемы; страдают многословностью записей; допускают неоднозначность толкования отдельных предписаний.
Псевдокод занимает промежуточное место между естественным и формальным языками. С одной стороны, он близок к обычному естественному языку, поэтому алгоритмы могут на нем записываться и читаться как обычный текст. С другой стороны, в псевдокоде используются некоторые формальные конструкции и математическая символика, что приближает запись алгоритма к общепринятой математической записи. В псевдокоде не приняты строгие синтаксические правила для записи команд, присущие формальным языкам, что облегчает запись алгоритма на стадии его проектирования и дает возможность использовать более широкий набор команд, рассчитанный на абстрактного исполнителя. Однако в псевдокоде обычно имеются некоторые конструкции, присущие формальным языкам, что облегчает переход от записи на псевдокоде к записи алгоритма на формальном языке. Ответ при этом получает человек, который выполняет команды согласно псевдокоду.
Приведем основные управляющие структуры псевдокода в табл. 1.1.
| Название структуры | Псевдокод |
|---|---|
| Присваивание |
переменная = число |
| Ввод |
ввод(переменная) |
| Вывод |
вывод(переменная)
вывод("фраза") |
| Ветвление |
если условие то действие1 иначе действие2 |
| Повторение |
пока условие начало пока действие конец пока |
Пример псевдокода:
алг Нахождение частного двух чисел
начало
вывод ("задайте делимое и делитель")
ввод (делимое, делитель)
если делитель ? 0
то частное = делимое / делитель
вывод(частное)
иначе вывод("нет решения")
кон алг Нахождение частного двух чиселВ данном примере используется три переменные: делимое, делитель и частное. Делимое и делитель задаются исполнителем произвольными числами. Частное считается лишь в том случае, если делитель не равен нулю.
Графическая реализация алгоритма представляет собой блок-схему. Блок-схема состоит из блоков определенной формы, соединенных стрелками. Ответ при этом получает человек, который выполняет команды согласно блок-схеме. Более подробно о блок-схемах будет рассказано в Лекции 2.
Программная реализация алгоритма – это компьютерная программа, написанная на каком-либо алгоритмическом языке программирования, например: С++, Pascal, Basic и т.д. Программа состоит из команд определенного языка программирования. Отметим, что одна и та же блок-схема может быть реализована на разных языках программирования. Ответ при этом получает ЭВМ, а не человек. Более подробно о составлении программ на языке программирования С++ смотреть Лекцию 3.
Различают три основных вида алгоритмов:
- линейный алгоритм,
- разветвляющийся алгоритм,
- циклический алгоритм.
Линейный алгоритм – это алгоритм, в котором действия выполняются однократно и строго последовательно.
Самый простой пример реализации линейного алгоритма – путь из университета домой.
Словесный способ записи данного алгоритма:
- выйти из университета на остановку;
- подождать нужный автобус;
- сесть на нужный автобус;
- оплатить проезд;
- выйти на требуемой остановке;
- дойти до дома.
Очевидно, что данный пример относится к линейному алгоритму, т.к. все действия следуют одно за другим, без условий и повторений.
Разветвляющийся алгоритм – это алгоритм, в котором в зависимости от условия выполняется либо одна, либо другая последовательность действий.
Самый простой пример реализации разветвляющегося алгоритма – если на улице идет дождь, то необходимо взять зонт, иначе не брать зонт с собой.
Приведенный выше пример псевдокода по нахождению частного двух чисел также относится к разветвляющемуся алгоритму.
Циклический алгоритм – это алгоритм, команды которого повторяются некое количество раз подряд.
Самый простой пример реализации циклического алгоритма – при чтении книги будут повторяться одни и те же действия: прочитать страницу, перелистнуть и т.д.
Более подробно о линейном, разветвляющемся и циклическом алгоритмах смотреть Лекцию 2.
Краткие итоги
Любая задача может быть разбита на элементарные действия. Для любой математической задачи или ситуации из жизни можно составить алгоритм решения. Алгоритм может быть описан словесно, псевдокодом, графически или программно. Задача всегда решается с помощью базовых типов алгоритма – линейного, разветвляющегося или циклического.
Вопросы
- Что такое алгоритм?
- В чем состоит задача алгоритмизации?
- Какими свойствами обладает алгоритм?
- Какие виды алгоритма бывают?
Упражнения
- Составьте алгоритмы по походу в магазин за яблоками. Используйте линейный и разветвляющийся алгоритмы. Реализуйте их словесно.
- Составьте алгоритм по нахождению корней квадратного уравнения через дискриминант. Используйте разветвляющийся алгоритм. Реализуйте его псевдокодом.

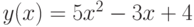 при
при 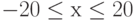 с шагом 0,5. Определите наименьшее значение функции и значение
с шагом 0,5. Определите наименьшее значение функции и значение  , при котором оно достигается.
, при котором оно достигается.