|
Постройте таблицу значений функции |
Реализация линейного и разветвляющегося алгоритмов
В данной лекции мы рассмотрим множество задач, соответствующих линейному и разветвляющемуся алгоритмам. В каждой задаче будут представлены блок-схемы, коды программ, а также результаты выполнения программ (консоли).
Занятие 1. Программная реализация линейного алгоритма
Пример 1. Даны числа 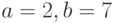 . Вычислить сумму
. Вычислить сумму  и разность
и разность  чисел
чисел  и
и  .
.
Приведем блок-схему на рис. 4.1.
Код программы (Visual Studio):
// proga10.cpp: определяет точку входа для консольного приложения.
//
#include "stdafx.h"
#include <iostream>
using namespace std;
int main()
{
double a, b, S, R;
a=2;
b=7;
S=a+b;
R=a-b;
cout<<"S="<<S<<endl;
cout<<"R="<<R<<endl;
return 0;
}Результат выполнения программы(Visual Studio):
Код программы (Borland C++):
#include <iostream.h>
int main(){
double a, b, S, R;
a=2;
b=7;
S=a+b;
R=a-b;
cout<<"S="<<S<<endl;
cout<<"R="<<R<<endl;
return 0;
}Результат выполнения программы (Borland C++):
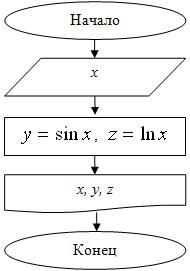
Пример 2. Составить блок-схему и программу для вычисления значений функций 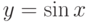 и
и 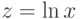 при
при  , который считывается с экрана (клавиатуры).
, который считывается с экрана (клавиатуры).
Приведем блок-схему на рис. 4.2.
Код программы (Visual Studio):
// proga11.cpp: определяет точку входа для консольного приложения.
//
#include "stdafx.h"
#include <iostream>
#include <math.h>
using namespace std;
int main(){
double x, y, z;
cout<<"vvedi x=";
cin>>x;
y=sin(x); z=log(x);
cout<<"pri x="<<x<<" y="<<y<<" z="<<z<<endl;
return 0;
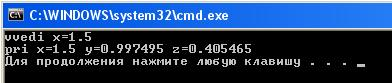
}Результат выполнения программы (Visual Studio):
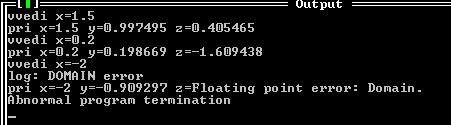
Ручной счет:
x=1.5 y=sin(1.5)=0.997495 z=ln(1.5)=0.405465
Результат выполнения программы (Visual Studio):
Ручной счет:
x=0.2 y=sin(0.2)=0.198669 z=ln(0.2)=-1.609438
Результат выполнения программы(Visual Studio):
Ручной счет:
x=-2 y=sin(-2)=-0.909297 z=ln(-2)=не существует, что соответствует результату на экране.
Код программы (Borland C++):
#include <iostream.h>
#include <math.h>
int main(){
double x, y, z;
cout<<"vvedi x=";
cin>>x;
y=sin(x);
z=log(x);
cout<<"pri x="<<x<<" y="<<y<<" z="<<z<<endl;
return 0;
}Результат выполнения программы(Borland C++):
Примечание. Чтобы не возникало ошибок при вычислении логарифма, надо поставить условие на аргумент  , поэтому данная задача будет рассмотрена ниже при реализации разветвляющегося алгоритма.
, поэтому данная задача будет рассмотрена ниже при реализации разветвляющегося алгоритма.
Когда требуется записать программно сложную математическую функцию, ее мысленно разбивают на внутреннюю и внешнюю. Например, если дано выражение 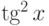 , то внешней функцией будет возведение в квадрат, а внутренней – тангенс от
, то внешней функцией будет возведение в квадрат, а внутренней – тангенс от  . Поэтому сначала начинают писать функцию возведения в степень: pow( , 2.0), а потом вписывают на первое место тангенс: pow( tan(x), 2.0).
. Поэтому сначала начинают писать функцию возведения в степень: pow( , 2.0), а потом вписывают на первое место тангенс: pow( tan(x), 2.0).
Когда требуется записать дробь, то ее мысленно разбивают на числитель и знаменатель. если в числителе или знаменателе стоит выражение, а не одно число или одна переменная, то все выражение берут в скобки: 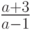 будет выглядеть в программе как
будет выглядеть в программе как  . Но дробь
. Но дробь 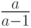 будет записана в виде
будет записана в виде  .
.
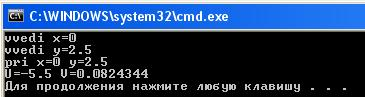
Пример 3. Составить блок-схему и программу для вычисления значений функций 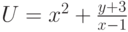 и
и 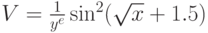 при различных значениях аргументов
при различных значениях аргументов 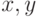 . Переменные
. Переменные 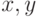 считать с клавиатуры.
считать с клавиатуры.
Блок-схема представлена на рис. 4.3.
Код программы (Visual Studio):
// proga12.cpp: определяет точку входа для консольного приложения.
//
#include "stdafx.h"
#include <iostream>
#include <math.h>
using namespace std;
int main(){
double x, y, U, V;
cout<<"vvedi x=";
cin>>x;
cout<<"vvedi y=";
cin>>y;
U=pow(x, 2.0)+(y+3.0)/(x-1.0);
V=1.0/pow(y, exp(1.0))*pow(sin(sqrt(x)+1.5), 2.0);
cout<<"pri x="<<x<<" y="<<y<<endl;
cout<<"U="<<U<<" V="<<V<<endl;
return 0;
}Результат выполнения программы (Visual Studio):
Результат выполнения программы (Visual Studio):
Код программы (Borland C++):
#include <iostream.h>
#include <math.h>
int main(){
double x, y, U, V;
cout<<"vvedi x=";
cin>>x;
cout<<"vvedi y=";
cin>>y;
U=pow(x,2.0)+(y+3.0)/(x-1.0);
V=1.0/pow(y,exp(1.0))*pow(sin(sqrt(x)+1.5),2.0);
cout<<"pri x="<<x<<" y="<<y<<endl;
cout<<"U="<<U<<" V="<<V<<endl;
return 0;
}Результат выполнения программы (Borland C++):
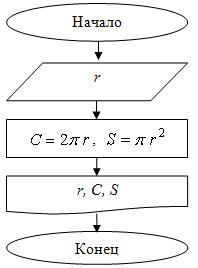
Пример 4. Найти длину окружности и площадь круга, если известен радиус.
Решение. Введем обозначения:  – радиус, который будет считываться с клавиатуры (т.к. он не задан конкретным числом);
– радиус, который будет считываться с клавиатуры (т.к. он не задан конкретным числом);  – длина окружности, вычисляемая по формуле
– длина окружности, вычисляемая по формуле  – площадь круга, вычисляемая по формуле
– площадь круга, вычисляемая по формуле 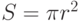 .
.
Приведем блок-схему на рис. 4.4.
Код программы (Visual Studio):
// proga13.cpp: определяет точку входа для консольного приложения.
//
#include "stdafx.h"
#include <iostream>
#include <math.h>
using namespace std;
int main(){
double r, C, S;
cout<<"vvedi r=";
cin>>r;
C=2.0*3.141593*r;
S=3.141593*pow(r, 2.0);
cout<<"r="<<r<<" C="<<C<<" S="<<S<<endl;
return 0;
}Результат выполнения программы (Visual Studio):
Код программы (Borland C++):
#include <iostream.h>
#include <math.h>
int main(){
double r, C, S;
cout<<"vvedi r=";
cin>>r;
C=2.0*M_PI*r;
S=M_PI*pow(r, 2.0);
cout<<"r="<<r<<" C="<<C<<" S="<<S<<endl;
return 0;
}Результат выполнения программы (Borland C++):










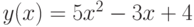 при
при 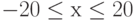 с шагом 0,5. Определите наименьшее значение функции и значение
с шагом 0,5. Определите наименьшее значение функции и значение  , при котором оно достигается.
, при котором оно достигается.